本文來自於論文Feiping Nie, Heng Huang, Xiao Cai, Chris H. Q. Ding. Efficient and Robust Feature Selection via Joint L2,1-Norms Minimization,NIPS,pp.1813-1821, 2010的閱讀心得總結

該論文提出了一種基於損失函式和正則項的L2,1$L_{2,1}$範數來實現一種高效、魯棒的特徵選擇方法，並提供了演算法分析和收斂性分析。
首先對比了L1$L_1$和L2$L_2$範數的特點：

• L1$L_1$和L2$L_2$範數表現出一種結構化的正則化技術，但是主要用於二分類；而L2,1範數則是用於多分類
• L2$L_2$範數對野點非常敏感，基於L2,1$L_{2,1}$範數的損失函式能夠去除野點
• L2$L_2$ 範數傾向於ω 的分量取值儘量均衡，即非零分量個數儘量稠密，而L0$L_0$ 範數和L1$L_1$範數，則傾向於ω 的分量儘量稀疏，即非苓分量個數儘量少

論文的創新點在於：

• 受到L2,1$L_{2,1}$範數的啟發，將L2,1$L_{2,1}$範數推廣到一般情況，即Lr,p$L_{r,p}$範數，同時證明了該範數滿足範數的三個條件。
  相關的討論為：
  
• 將損失函式的優化問題寫成一種矩陣的形式，對利用Lagrange對該問題進行了優化，提出了一種比較有效、快速的演算法。

首先是，將損失函式的L2$L_2$範數全部轉化為L2,1$L_{2,1}$範數，即可以同步優化，為後面的優化過程提供了條件。

在該最小化目標函式的優化中，等價轉化優化問題：

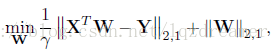
更進一步：

寫成矩陣形式：

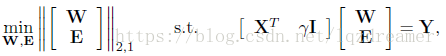
記：
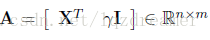
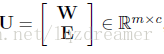
即為

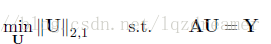
利用Lagrange方法，轉化為：

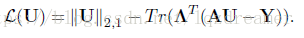
求導（相關求導公式可以檢視另外一篇部落格） 矩陣L2,1範數及矩陣L2,p範數的求導：

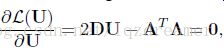
其中

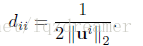
是對角陣，即有：

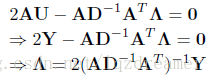
結合上式即有

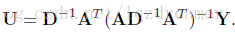
此時U即為全域性最優解，由於D矩陣中包含有U，因此需要迭代求解。演算法步驟為：

關於迭代求解的收斂性證明（證明過程看論文），主要運用了引理：

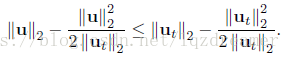
同時，將該優化問題推廣到更一般的情況（D仍為對角陣，f(U)是凸函式）：

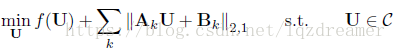
迭代式：

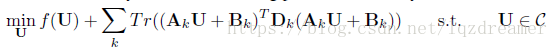
該演算法對基因組和蛋白質組生物標誌物進行了實驗，取得了高效、高準確度的效果。