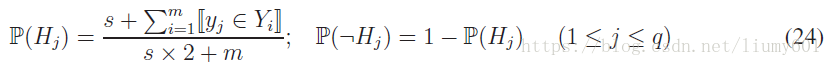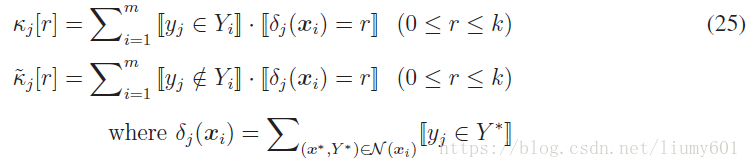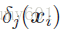最近有一個專案需要用多標籤分類思想來建模，之前對這塊不是太瞭解，查了一些論文，發現目前主流的演算法包括ML-KNN、ML-DT、Rank-SVM、CML等，其中ML-KNN演算法思想最簡單，結合原始論文，本文大概介紹下演算法思想和程式碼實現。

      ML-KNN借鑑了KNN的思想尋找K個近鄰樣本，並運用貝葉斯條件概率，來計算當前標籤為1和0的概率，概率大的標籤定為樣本最終的標籤，這就是ML-KNN的大致思想。

      虛擬碼如下：

1、第1到3行計算樣本集中每個樣本的K個最近鄰。

2、第4到6行計算每個標籤出現的概率

其中Hj表示標籤j出現這一事件，m表示樣本總數，s是平滑項，通常取1。Kj[r]陣列表示當前標籤為1並且K相鄰樣本中標籤為1的個數為r的樣本總數。

3、第8行計算未知樣本的K近鄰

4、第9、10行計算未知樣本K近鄰中標籤j為1的個數

5、第12行計算未知樣本的每個標籤

其中P(Hj|Cj)表示未知樣本K近鄰中標籤j為1個數為Cj條件下，該樣本標籤j也為1的概率，P(Hj)表示樣本集中標籤j為1的概率，P(Cj|Hj)表示當前樣本標籤j為1條件下，K近鄰中標籤j為的個數為Cj的概率。

Python程式碼實現如下：

import numpy as np
import pandas as pd

def mlknn(train, test, id, label_columns, k):
	smooth = 1.0
	#計算每個標籤出現的概率
	phj = {}
	for label in label_columns:
		phj[label] = (smooth+train[train[label]==1].shape[0])/(smooth*2+train.shape[0])
	
	train_ids = train[id].values
	tmp_train = train.drop(label_columns+[id], axis=1)
	test_ids = test[id].values
	test_labels = test[label_columns]
	tmp_test = test.drop(label_columns+[id], axis=1)	
	data_columns = tmp_train.columns
	
	#計算訓練集每個樣本之間的相似度，並儲存跟每個樣本最相似的K個樣本
	knn_records_train = {}
	cos_train = {}
	for i in range(tmp_train.shape[0]):
		record = tmp_train.iloc[i]
		norm = np.linalg.norm(record)
		cos_train[train_ids[i]] = {}
		
		for j in range(tmp_train.shape[0]): 
			if cos_train.has_key(train_ids[j]) and cos_train[train_ids[j]].has_key(train_ids[i]):
				cos_train[train_ids[i]][train_ids[j]] = cos_train[train_ids[j]][train_ids[i]]
			else:
				cos = np.dot(record, tmp_train.iloc[j])/(norm*np.linalg.norm(tmp_train.iloc[j]))
				cos_train[train_ids[i]][train_ids[j]] = cos
		topk = sorted(cos_train[train_ids[i]].items(), key=lambda item:item[1], reverse=True)[0:k]
		knn_records_train[train_ids[i]] = [item[0] for item in topk]

	kjr = {}
	not_kjr = {}
	for label in label_columns:
		kjr[label] = {}
		not_kjr[label] = {}
		for m in range(train.shape[0]):
			record = train.iloc[m]
			if record[label]==1:
				#計算標籤為1並且相鄰K個樣本中標籤也為1的樣本個數
				r = 0
				for rec_id in knn_records_train[train_ids[m]]:
					if train[train[id]==rec_id][label].values[0]==1:
						r += 1
				if not kjr[label].has_key(r):
					kjr[label][r] = 1
				else:
					kjr[label][r] += 1
			else:
				#計算標籤為0並且相鄰K個樣本中標籤也為1的樣本個數
				r = 0
				for rec_id in knn_records_train[train_ids[m]]:
					if train[train[id]==rec_id][label].values[0]==1:
						r += 1
				if not not_kjr[label].has_key(r):
					not_kjr[label][r] = 1
				else:
					not_kjr[label][r] += 1
	
	#計算當前樣本標籤為1條件下，K個近鄰樣本中標籤為1個數為Cj的概率
	pcjhj = {}
	for label in label_columns:
		pcjhj[label] = {} 
		for L in range(k+1):
			if kjr[label].has_key(L):
				pcjhj[label][L] = (smooth+kjr[label][L])/(smooth*(k+1)+sum(kjr[label].values()))
			else:
				pcjhj[label][L] = (smooth+0)/(smooth*(k+1)+sum(kjr[label].values()))
	
	#計算當前樣本標籤為0條件下，K個近鄰樣本中標籤為1個數為Cj的概率
	not_pcjhj = {}
	for label in label_columns:
		not_pcjhj[label] = {} 
		for L in range(k+1):
			if not_kjr[label].has_key(L):
				not_pcjhj[label][L] = (smooth+not_kjr[label][L])/(smooth*(k+1)+sum(not_kjr[label].values()))
			else:
				not_pcjhj[label][L] = (smooth+0)/(smooth*(k+1)+sum(not_kjr[label].values()))
	
	#計算測試集中每個樣本與訓練集樣本之間的相似度，並儲存跟每個樣本最相似的K個樣本
	knn_records_test = {}
	cos_test = {}
	for i in range(tmp_test.shape[0]):
		record = tmp_test.iloc[i]
		norm = np.linalg.norm(record)
		cos_test[test_ids[i]] = {}
		
		for j in range(tmp_train.shape[0]): 
			cos = np.dot(record, tmp_train.iloc[j])/(norm*np.linalg.norm(tmp_train.iloc[j]))
			cos_test[test_ids[i]][train_ids[j]] = cos
		topk = sorted(cos_test[test_ids[i]].items(), key=lambda item:item[1], reverse=True)[0:k]
		knn_records_test[test_ids[i]] = [item[0] for item in topk]

	pred_test_labels = {}
	correct_rec = 0
	for i in range(tmp_test.shape[0]):
		record = tmp_test.iloc[i]
		correct_col = 0
		for label in label_columns:
			if not pred_test_labels.has_key(label):
				pred_test_labels[label] = []
			#計算每個測試樣本K近鄰中標籤為1的個數
			cj = 0
			for rec_id in knn_records_test[test_ids[i]]:
				if train[train[id]==rec_id][label].values[0]==1:
						cj += 1
			#計算包含Cj個標籤為1的K近鄰條件下，該測試樣本標籤為1的概率
			phjcj = phj[label]*pcjhj[label][cj]
			#計算包含Cj個標籤為1的K近鄰條件下，該測試樣本標籤為0的概率
			not_phjcj = (1-phj[label])*not_pcjhj[label][cj]
			
			if phjcj>not_phjcj:
				pred_test_labels[label].append(1)
				pred_label = 1
			else:
				pred_test_labels[label].append(0)
				pred_label = 0
			if pred_label==test_labels[label].values[i]:
				correct_col += 1
		if correct_col==len(label_columns):
			correct_rec += 1
			
	print '測試集標籤識別準確率', correct_rec*1.0/test.shape[0]