深度學習筆記8 資料預處理
阿新 • • 發佈:2019-01-02
資料預處理標準流程
- 自然灰度影象
(1)灰度影象具有平穩特性,對每個資料樣本分別做均值消減(即減去直流分量)——每個影象塊,計算平均畫素值,並將影象每個畫素點減去均值。每個影象塊有一個不同的均值。
x=x-repmat(mean(x,1),size(x,1),1);%x是144*10000,代表10000個patch
(2)然後採用PCA/ZCA白化處理,其中的epsilon要足夠大以達到低通濾波的作用。epsilon值如何取,教程上說:
一種檢驗 epsilon 是否合適的方法是用該值對資料進行 ZCA 白化,然後對白化前後的資料進行視覺化。如果 epsilon 值過低,白化後的資料會顯得噪聲很大;相反,如果 epsilon 值過高,白化後的資料與原始資料相比就過於模糊。一種直觀上得到 epsilon 大小的方法是以圖形方式畫出資料的特徵值,如下圖的例子所示,你可以看到一條”長尾”,它對應於資料中的高頻噪聲部分。你需要選取合適的 epsilon,使其能夠在很大程度上過濾掉這條”長尾”,也就是說,選取的 epsilon 應大於大多數較小的、反映資料中噪聲的特徵值。
如原始資料是x
sigma=x*x'./size(x,2);
[u,s,v]=svd(sigma);
plot(1:size(sigma,1),diag(s));
顯示原資料的特徵值曲線:
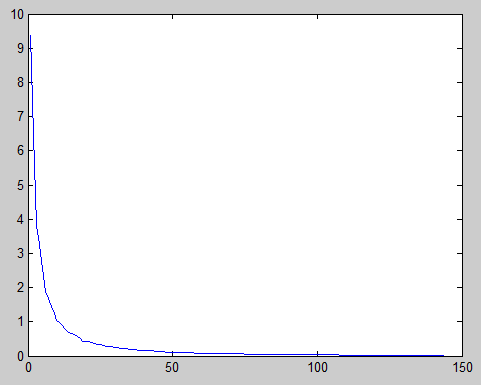
可以看到大約第50個特徵值後面的部分要過濾掉,因此,epsilon>=第50個特徵值就可以了。
>> s(50,50)
ans =
0.1080可以取epsilon=0.1080,教程上的程式碼給的值是epsilon=0.1,看來這個方法還是很有效的。
- 彩色影象
(1)對於彩色影象,色彩通道間並不存在平穩特性。因此首先對資料進行特徵縮放(使畫素值在[0,1]間)。對於影象[0,255],可將畫素值除以255.
(2)對特徵進行分量均值歸零化
從下面程式碼中可看到是對同一通道的對應畫素點(即特徵)進行均值歸零。——這屬於特徵標準化。
特徵標準化:
首先計算每一維度上資料的均值(使用全體資料),之後再每個維度上減去該均值。下一步便是在資料的每一維度上除以該維度上資料的標準差。對於自然影象,方差歸一化不用進行。
(3)使用足夠大的epsilon來做PCA/ZCA。
——參考linearDecoderExercise.m
% Subtract mean patch (hence zeroing the mean of the patches)
meanPatch = mean(patches, 2); %patches' size :192*10000 ,即10000個8*8*3塊 執行:
plot(1:size(s,1),diag(s))結果:
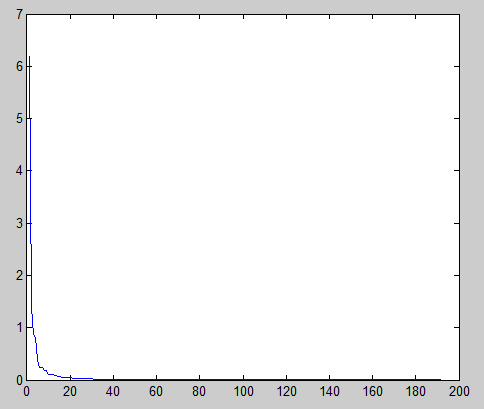
要濾掉長尾,選第十幾個特徵值很合適。可選episilon=s(12,12)=0.0962.練習上給的是epsilon=0.1,看來這個方法還是比較靠譜的。~~呵呵
白化
- 基於重構的模型
episilon的選擇就採用上面的方式——濾掉“長尾”。 - 基於正交化ICA的模型
對基於正交化ICA的模型來說,保證輸入資料儘可能地白化(即協方差矩陣為單位矩陣)非常重要。這是因為:這類模型需要對學習到的特徵做正交化,以解除不同維度之間的相關性(詳細內容請參考 ICA 一節)。因此在這種情況下,epsilon 要足夠小(比如 epsilon = 1e − 6)。
在上例採用epsilon=1e-6時,ZCA後的資料協方差矩陣,圖示:
如果是單位矩陣,就是1對應的一條直線,而現在接近單位矩陣。 - 注意: 在使用分類框架時,我們應該只基於練集上的資料計算PCA/ZCA白化矩陣。需要儲存以下兩個引數留待測試集合使用:(a)用於零均值化資料的平均值向量;(b)白化矩陣。測試集需要採用這兩組儲存的引數來進行相同的預處理。
例:在linearDecoderExercise.m中,可以看到,把ZCA白化後的patches訓練稀疏自編碼器,儲存了 ‘ZCAWhite’, ‘meanPatch’。這樣當後面在有影象通過該稀疏自編碼器提取特徵時,就要和訓練時一樣的白化矩陣和平均值。
theta = initializeParameters(hiddenSize, visibleSize);
% Use minFunc to minimize the function
addpath minFunc/
options = struct;
options.Method = 'lbfgs';
options.maxIter = 400;
options.display = 'on';
[optTheta, cost] = minFunc( @(p) sparseAutoencoderLinearCost(p, ...
visibleSize, hiddenSize, ...
lambda, sparsityParam, ...
beta, patches), ...
theta, options);
% Save the learned features and the preprocessing matrices for use in
% the later exercise on convolution and pooling
fprintf('Saving learned features and preprocessing matrices...\n');
save('STL10Features.mat', 'optTheta', 'ZCAWhite', 'meanPatch');