2. 程式人生 > >C++模板實現的AVL樹

C++模板實現的AVL樹

阿新 • • 發佈：2019-01-02

1 AVL樹的定義

AVL樹是一種自平衡二叉排序樹，它的特點是任何一個節點的左子樹高度和右子樹的高度差在-1,0,1三者之間。AVL樹的任何一個子樹都是AVL樹。

2 AVL樹的實現

AVL樹本質是一種二叉排序樹，所以二叉排序樹的任何性質AVL樹都具有，但是AVL樹稍微複雜的地方就是AVL樹必須滿足平衡條件，具體跟BST不同的地方主要體現在插入，刪除操作。

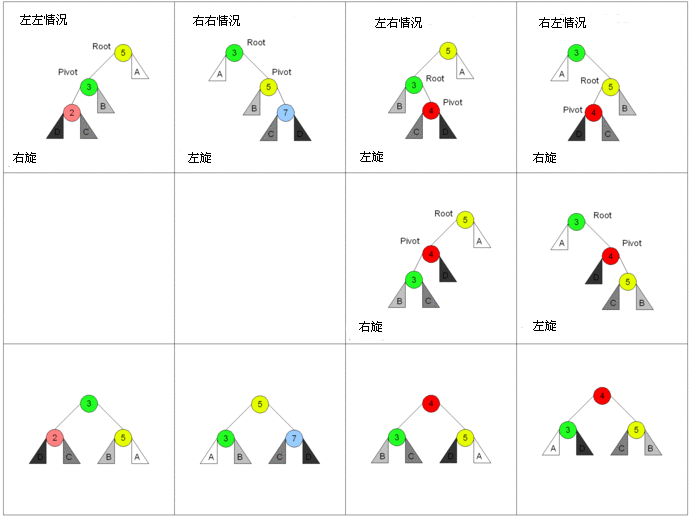
插入操作：當插入之後可能會出現不平衡，所以這時候要通過旋轉樹來實現平衡。旋轉有四種類型，左左，左右，右左，右右。其中左左旋轉和右右旋轉是映象的，左右旋轉和右左旋轉是映象的，所以實質上就是兩種型別的旋轉。針對左左旋轉，只需要旋轉一次即可，針對左右旋轉，需要執行兩次旋轉。見下圖：


這裡採用遞迴法實現插入和刪除操作。使用遞迴方便的一點是如果函式的引數是引用型別的，當傳入一個p->left的時候，我們在當前函式的下層遞迴的時候，對p進行的賦值操作其實就是對上層遞迴中的p->left進行的操作，所以這樣就不需要傳遞父指標了。

3 實現程式碼

//AVLTree.h

#ifndef DDXX_AVLTREE_H
#define DDXX_AVLTREE_H
#include <iostream>
#include <queue>
using namespace std;
template<typename Type>
class AVLTree
{
	struct Node
	{
		Type e;
		Node* left;
		Node* right;
		int h;
		Node(Type _e):e(_e),left(NULL),right(NULL),h(0){}
		Node(Type _e,Node* _left,Node* _right,int _h):e(e),left(_left),right(_right),h(_h){}
	};
public:
	AVLTree();
	AVLTree(Type arr[],int nLength);
	/*AVLTree(const AVLTree& right);
	AVLTree& operator=(const AVLTree& right);*/
	~AVLTree();
public:
	bool	insert(Type e,Node* &p);
	void	erase(Type e,Node* &p);
	Node*&	find(Type e)const;
	void	traverse(Node* p)const;
	void	traverseByLevel(Node* p)const;
	int		getLength(){return mLength;}
	Node*&	getParent(Node* p);
	Node*&	getRoot(){return mRoot;} //notice the return type
	bool	empty(){return mRoot==NULL;};
	void	clear();
	void	clears(Node* &p);
private:
	void	rotateLeft(Node* &k2);
	void	rotateRight(Node* &k2);
	void	rotateLeftDouble(Node* &p);
	void	rotateRightDouble(Node* &p);
	int		height(Node* p)const{ return p == NULL ? -1 : p->h ;}
	int		max(int x,int y){return x>y?x:y;}
private:
	Node* mRoot;
	int mLength;

};
template<typename Type> AVLTree<Type>::AVLTree():mRoot(NULL),mLength(0)
{
}

template<typename Type> AVLTree<Type>::AVLTree(Type arr[],int nLength):mRoot(NULL),mLength(0)
{
	for(int i=0;i<nLength;i++)
	{
		insert(arr[i],mRoot);
	}
}

template<typename Type> AVLTree<Type>::~AVLTree()
{
	clears(mRoot);
}
template<typename Type> bool AVLTree<Type>::insert(Type e,Node* &p)
{
	if( p== NULL)
	{
		p = new Node(e);
		mLength++;
	}
	else if(e < p->e)
	{
		insert(e,p->left);
		if( height(p->left) - height(p->right) == 2)
		{
			if (e < p->left->e)
				rotateLeft(p);
			else
				rotateLeftDouble(p);
		}
	}
	else if(e > p->e)
	{
		insert(e,p->right);
		if( height(p->left) - height(p->right) == -2)
		{
			if (e > p->right->e)
				rotateRight(p);
			else
				rotateRightDouble(p);
		}
	}
	else // e ia already exist
	{	
		//return false;
	}
	p->h = max( height(p->left),height(p->right) )+1;
	return true;
}

template<typename Type> void AVLTree<Type>::rotateLeft(Node*& k2)
{
	Node* k1 = k2->left;
	k2->left = k1->right;
	k1->right = k2;

	k1->h = max( height(k1->left),height(k1->right) ) + 1;
	k2->h = max( height(k2->left),height(k2->right) ) + 1;
	k2 = k1;// join the original node
}

template<typename Type> void AVLTree<Type>::rotateRight(Node* &k2)
{
	Node* k1 = k2->right;
	k2->right = k1->left;
	k1->left = k2;

	k1->h = max( height(k1->left),height(k1->right) ) + 1;
	k2->h = max( height(k2->left),height(k2->right) ) + 1;
	//k1=k2，因為在insert函式中傳入的是p->left或者p->right的引用，所以這裡能把根結點賦給其父結點的子節點
	k2 = k1;
}

template<typename Type> void AVLTree<Type>::rotateLeftDouble(Node*& k3)
{
	rotateRight(k3->left);
	rotateLeft(k3);
}
template<typename Type> void AVLTree<Type>::rotateRightDouble(Node*& k3)
{
	rotateLeft(k3->right);
	rotateRight(k3);
}

template<typename Type> void AVLTree<Type>::traverse(Node* p)const
{
	if( p == NULL)
		return;
	else
	{
		traverse(p->left);
		cout<<"element:"<<p->e<<endl; //traverse by mid
		traverse(p->right);	
	}
}

template<typename Type> void AVLTree<Type>::traverseByLevel(Node* root)const
{
	if(root == NULL)
	{
		cout<<"The tree is empty"<<endl;
		return;
	}
	queue<Node*> que;
	que.push(root);
	while( !que.empty() )
	{
		Node* ptr = que.front();
		que.pop();
		cout<<"element:"<<ptr->e<<"	th:"<<height(ptr->left) - height(ptr->right)<<endl;
		if(ptr->left != NULL)
			que.push(ptr->left);
		if(ptr->right != NULL)
			que.push(ptr->right);
	}
}

template<typename Type> typename AVLTree<Type>::Node* & AVLTree<Type>::getParent(Node* p)
{  
    if( p == m_root)  
        return NULL;  
    Node* ptr = m_root;  
    Node* ptf = ptr;  
    while( ptr != NULL )  
    {  
        if ( ptr->e == p->e )  
            return ptf;  
        if ( ptr->e > p->e )  
        {  
            ptf = ptr;  
            ptr = ptr->leftChild;  
        }  
        else  
        {  
            ptf = ptr;  
            ptr = ptr->rightChild;
        }  
    }   
}

template<typename Type> typename AVLTree<Type>::Node*& AVLTree<Type>::find(Type e)const
{  
    Node* ptr = m_root;  
  
    while(ptr != NULL)  
    {  
        if ( ptr->e == e )  
            return ptr;  
        if ( ptr->e > e )  
            ptr = ptr->leftChild;  
        else  
            ptr = ptr->rightChild;  
    }  
    //if ( ptr == NULL )  
    return NULL;  
}

template<typename Type> void AVLTree<Type>::clears(Node*& p)
{
	if( p == NULL )
		return;
	else
	{
		clears(p->left);
		clears(p->right);
		delete p;
		p = NULL;
		mLength--;
	}
}

template<typename Type> void AVLTree<Type>::clear()
{
	clears(mRoot);
}

template<typename Type> void AVLTree<Type>::erase(Type e,Node* &p)
{
	if( p == NULL)
		return;
	if( e > p->e)
	{
		erase(e,p->right);
		if( height(p->left) - height(p->right) == 2)
		{
			if( height(p->left->left) > height(p->left->right) )
				rotateLeft(p);
			else
				rotateLeftDouble(p);
		}
	}
	else if( e < p->e)
	{
		erase(e,p->left);
		if( height(p->left) - height(p->right) == -2)
		{
			if( height(p->right->right) > height(p->right->left) )
				rotateRight(p);
			else
				rotateRightDouble(p);
		}
	}
	else if ( e == p->e && p->left!= NULL && p->right!= NULL)
	{
		Node* pmax = p->left;
		while( pmax->right != NULL)
		{
			pmax = pmax->right;
		}
		p->e = pmax->e;
		erase(p->e,p->left);
	}
	else //最終的刪除會在這裡執行
	{
		Node* pNew = p->left==NULL ? p->right : p->left;
		delete p;
		p = pNew;
		mLength--;
	}
	if ( p!=NULL)
		p->h = max( height(p->left),height(p->right)) + 1;
}
#endif

//main.cpp 
#include <iostream>
#include "AVLTree.h"
using namespace std;

void main()
{
	int Arr[9] = {6,2,8,4,10,0,12,16,14};
	AVLTree<int> Tr(Arr,9);
	Tr.traverse(Tr.getRoot());
	Tr.traverseByLevel(Tr.getRoot());

	Tr.erase(14,Tr.getRoot());
	Tr.traverse(Tr.getRoot());
	Tr.traverseByLevel(Tr.getRoot());
	cout<<"Tree's length is:"<<Tr.getLength()<<endl;
	Tr.clear();
	cout<<"Tree's length is:"<<Tr.getLength()<<endl;

}

4 測試結果



相關推薦

資料結構之：AVL樹詳解及C++模板實現

AVL樹簡介AVL樹的名字來源於它的發明作者G.M. Adelson-Velsky 和 E.M. Landis。AVL樹是最先發明的自平衡二叉查詢樹（Self-Balancing Binary Search Tree,簡稱平衡二叉樹）。一棵AVL樹有如下必要條件：條件一：它必

C++模板實現的AVL樹

1 AVL樹的定義 AVL樹是一種自平衡二叉排序樹，它的特點是任何一個節點的左子樹高度和右子樹的高度差在-1,0,1三者之間。AVL樹的任何一個子樹都是AVL樹。 2 AVL樹的實現 AVL樹本質是一種二叉排序樹，所以二叉排序樹的任何性質AVL樹都具有，但是AVL樹稍微複雜

使用C++實現AVL樹模板

今天練習編寫了一下AVL樹。參考了Weiss的資料結構與演算法C++描述版。上一個實現了一般的二叉搜尋樹，在使用的過程中可能會慢慢變得不平衡，這樣很可能會降低查詢、插入等等的效率，因此我們需要使用演算法來實現樹的平衡。AVL樹是一種比較經典的平衡二叉搜尋樹，它規定每個節點的

C++模板實現二叉樹(六 AVL樹基礎與旋轉)

dsw演算法可以從全域性平衡樹,但是,往往在插入於刪除動作發生時,將隻影響樹的一部分,此時重新平衡可以只在樹的一部分進行.AVL樹要求每個節點左右子樹的高度差最大為1.平衡因子用右子樹的高度減去左子樹的高度.在AVL樹中,平衡因子應該只有-1,0,1三種選擇.只

資料結構圖文解析之：樹的簡介及二叉排序樹C++模板實現.

  閱讀目錄 0. 資料結構圖文解析系列 1. 樹的簡介 1.1 樹的特徵 1.2 樹的相關概念 2. 二叉樹簡介 2.1 二叉樹的定義 2.2 斜樹、滿二叉樹、完全二叉樹、二叉查詢樹 2

資料結構圖文解析之：哈夫曼樹與哈夫曼編碼詳解及C++模板實現

0. 資料結構圖文解析系列 1. 哈夫曼編碼簡介 哈夫曼編碼（Huffman Coding）是一種編碼方式，也稱為“赫夫曼編碼”，是David A. Huffman1952年發明的一種構建極小多餘編碼的方法。 在計算機資料處理中，霍夫曼編碼使用變長編碼表對源符號進行編碼，出現頻率較高的源符號採用較短的編碼，

C++模板實現二叉樹(五 樹的平衡之dsw演算法)

二叉樹的高效查詢演算法依賴於樹的平衡.如果樹高度不平衡,二叉樹將退化成類似連結串列的效率,則二叉樹的優勢就不存在了.平衡二叉樹的dsw演算法提供了一種將二叉樹轉化成平衡二叉樹的方法. 演算法的核心思想是利用旋轉. 1.通過右旋轉生成主鏈. 2.通過左旋轉生

C++模板實現單鏈表

#include "ListNode.h" template<typename Type> class SingleList{ public: SingleList():head(new ListNode<Type>()){} ~SingleList(){ MakeEmpty

棧（鏈式儲存） C++模板實現

#include <iostream> using namespace std; //棧結點類 template <typename T> class stackNode{ private: T data; //結點資料部分 stackN

資料結構圖文解析之：佇列詳解與C++模板實現

正文 回到頂部 0. 資料結構圖文解析系列 回到頂部 1. 佇列簡介 回到頂部 1.1 佇列的特點 佇列（Queue）與棧一樣，是一種線性儲存結構，它具有如下特點： 佇列中的資料元素遵循“先進先出”（First In First Out）的原則，簡稱FI

C++模板實現棧的基本操作

第一種是模板實現： #pragma once #include<iostream> using namespace std; #include"Vector.h" template<

C++模板實現棧

儘管C++的STL庫裡面有Stack類，但是本著學習的目的，在參考他人成果的基礎上，我決定自己實現一次。這個實現採用的是”連結串列+動態記憶體+模板”的方式實現。眾所周知，棧是一種後進先出的資料結構，即先入棧的元素最後出棧，最後入棧的元素最先出棧。棧常常使用在計

C++模板實現佇列（2）

迴圈佇列中新增和刪除元素時並不像鏈式佇列那樣使用動態記憶體分配，一般採用固定的佇列長度，一次分配一片記憶體用於儲存資料，等到佇列使用完畢後釋放掉即可。記憶體使用效率比鏈式佇列高，也比較容易實現。佇列的資料定義如下： unsigned int size;

抽象性設計——用C語言實現B樹的基本操作

這次做的是資料結構的一個抽象性實驗，我選擇的是B樹的基本操作。 編譯環境是：VS 2015 BTree.h #include<stdio.h> #include<stdlib.h> #include<time.h> #defi

資料結構圖文解析之：二叉堆詳解及C++模板實現

0. 資料結構圖文解析系列 1. 二叉堆的定義 二叉堆是一種特殊的堆，二叉堆是完全二叉樹或近似完全二叉樹。二叉堆滿足堆特性：父節點的鍵值總是保持固定的序關係於任何一個子節點的鍵值，且每個節點的左子樹和右子樹都是一個二叉堆。 當父節點的鍵值總是大於或等於任何一個子節點的鍵值時為最大堆。 當父節點的鍵值總是小於

資料結構圖文解析之：陣列、單鏈表、雙鏈表介紹及C++模板實現

0. 資料結構圖文解析系列 1. 線性表簡介 線性表是一種線性結構，它是由零個或多個數據元素構成的有限序列。線性表的特徵是在一個序列中，除了頭尾元素，每個元素都有且只有一個直接前驅，有且只有一個直接後繼，而序列頭元素沒有直接前驅，序列尾元素沒有直接後繼。 資料結構中常見的線性結構有陣列、單鏈表、雙鏈表、迴圈

資料結構圖文解析之：棧的簡介及C++模板實現

0. 資料結構圖文解析系列 1. 棧的簡介 1.1棧的特點 棧(Stack)是一種線性儲存結構，它具有如下特點： 棧中的資料元素遵守”先進後出"(First In Last Out)的原則，簡稱FILO結構。 限定只能在棧頂進行插入和刪除操作。 1.2棧的相關概念 棧的相關概念： 棧頂與棧底：允許元素

連結串列——用C++模板實現

LinkedList.h //單向連結串列的實現 //查詢、插入和移除某個元素、複製、清空單向連結串列的時間複雜度均為O(n) //設計類時，應儘量減少類的成員函式之間的依賴關係 #ifndef LINKEDLIST_H #define LINKEDLIST_H templa

棧（順序儲存）C++模板實現

#include <iostream> using namespace std; template <typename T> class stack{ private: int top; //棧頂指標 int maxLen; //棧最大

圖的鄰接表儲存（C++模板實現）

一，鄰接表表示法 圖的鄰接矩陣儲存方法跟樹的孩子連結串列示法相類似，是一種順序分配和鏈式分配相結合的儲存結構。鄰接表由表頭結點和表結點兩部分組成，其中圖中每個頂點均對應一個儲存在陣列中的表頭結點。如這個表頭結點所對應的頂點存在相鄰頂點，則把相鄰頂點依次存放於表頭結點所指向的