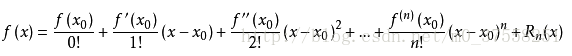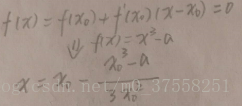牛頓迭代法求解一個數的n次方根
1.泰勒展開
n階可微函式f(x)在x=x0處的展開為
2.牛頓迭代法
對於求a的立方根,可以設f(x)=x^3-a,從而轉換成求解f(x)=0,即求方程的根。
對於求a的平方根,設f(x)=x^2-a,從而轉換成求解f(x)=0
初始化可以令x0=1,當兩次求解的差的絕對值小於0.000001時,認為結果可以接受。
3.Java實現(立方根)
public static double getCubeRoot(double input) { double x0 = 1; double x1 = x0 - (x0 - input/(x0*x0)) / 3; while(Math.abs(x1-x0) > 0.000001) { x0 = x1; x1 = x0 - (x0 - input/(x0*x0)) / 3; } return x1; }
相關推薦
牛頓迭代法求解一個數的n次方根
1.泰勒展開n階可微函式f(x)在x=x0處的展開為2.牛頓迭代法對於求a的立方根,可以設f(x)=x^3-a,從而轉換成求解f(x)=0,即求方程的根。對於求a的平方根,設f(x)=x^2-a,從而轉換成求解f(x)=0初始化可以令x0=1,當兩次求解的差的絕對值小於0.0
牛頓迭代法求求一個數的算術平方根
產生背景: 牛頓迭代法(Newton's method)又稱為牛頓-拉夫遜方法(Newton-Raphson method),它是牛頓在17世紀提出的一種在實數域和複數域上近似求解方程的方法。多數方程不存在求根公式,因此求精確根非常困難,甚至不可能,從而尋找方程的近似根就顯得特別重要。方法使用函式f(x)的泰
使用牛頓迭代法求解n次方根
一、牛頓迭代法的原理 1.定義摘自百度百科: 因此,我們的f(x)=xn f '(x)=nxn-1 . 2.java實現 import java.util.Scanner; public class NewtonMetho
利用牛頓迭代法求解非線性方程組
最近一個哥們,是用牛頓迭代法求解一個四變數方程組的最優解問題,從網上找了程式碼去改進,但是總會有點不如意的地方,迭代的次數過多,但是卻沒有提高精度,真是令人揪心! 經分析,
牛頓迭代法求解方程
說明:該篇部落格源於博主的早些時候的一個csdn部落格中的一篇,由於近期使用到了,所以再次作一總結。原文地址 概述 牛頓迭代法(Newton’s method)又稱為牛頓-拉夫遜(拉弗森)方法(Newton-Raphson method),它是牛頓在17
牛頓迭代法(含輾轉相除法原理):近似求解方程的根
結論:迭代序列: x (n+1)= x (n)- f ( x(n) ) / f '( x(n) ) (附C++程式碼) (通過不斷作切線找切線與x軸交點重複,交點不斷向根逼近) 牛頓迭代法:在實數和複數域求方程的近似根,由泰勒級數前幾項尋找 計算方法: 設 x
求解一元多次方程的兩種方法:牛頓迭代法和二分法
求解方程x*x*x-2*x-1=0,C語言實現 一:牛頓迭代法,牛頓迭代法是從泰勒公式中取前兩項構成線性近似方程,從x0開始,一步一步接近近似解,直到誤差在限定範圍內。 //牛頓迭代法求求解方程的根 #include <stdio.h> #include &l
數學建模三 單變數優化和求解 牛頓迭代法
#include<iostream> #include<cmath> using namespace std; double f(double x); double f1(do
利用牛頓迭代法 求n次方根
牛頓迭代法 這裡不多說,直接上程式碼: 求平方根: public static double getPingFangRoot(double input){ if(input==0) return 0; double x0,x1; x0=input;
快速求解方程的根——二分法與牛頓迭代法
本文始發於個人公眾號:**TechFlow**,原創不易,求個關注 今天是週四高等數學專題的第7篇文章。 之前的文章和大家聊了許多數學上的理論,今天和大家聊點有用的東西。 我們都知道,工業上的很多問題經過抽象和建模之後,本質還是數學問題。而說到數學問題就離不開方程,在數學上我們可以用各種推算、公式,但是
K Best POJ - 3111 (牛頓迭代法)
傳送門 題意:有n個物品的重量和價值分別是wi和vi。從中選出k個物品使得單位重量的價值最大。 題解:先取前k個元素算出S0 =∑(vi/wi) 作為初始值,然後對每一個元素(n個)求yi=vi-s0*wi,對yi從大到小排序,取前k個元素算出S,重複上面的運算(每次迴圈後把S的值賦給S0,
【R語言-20行程式碼】牛頓迭代法求伽馬函式極大似然估計法的引數估計
簡述 研究了下計算公式,簡化了一下,用r語言實現了。 演算法解釋 牛頓迭代法 x
基於matlab的Guass-Seidel(高斯--賽德爾) 迭代法求解線性方程組
演算法解釋見此:https://blog.csdn.net/zengxyuyu/article/details/53056453 原始碼在此: main.m clear clc A = [8 -3 2;4 11 -1;6 3 12]; b = [20;33;36]; [
基於matlab的jacobi(雅可比)迭代法求解線性方程組
說明推導見此部落格:https://blog.csdn.net/zengxyuyu/article/details/53054880 原始碼見下面: main.m clear clc A = [8 -3 2;4 11 -1;6 3 12]; b = [20;33;36]; [x, n]
牛頓迭代法求根
三次方根 (cube.pas/c/cpp) 【問題描述】 自從在第2題中老師們的工作積極性提高以來,以Fengzee為首的學生們苦不堪言,因為老師給他們留了太多的作業,有些作業甚至是幾乎無法完成的。這次,數學老師佈置下了10道開三次方的作業題,要求同學們筆算完成。Fengzee當然不會花時間做這種沒用的
計算平方根【牛頓迭代法】
計算任意數字的平方根 import java.util.*; import java.math.*; public class Main{ public static double sqrt(double c) { if(c<0) return Double.NaN; d
zoj-4005(牛頓迭代法|手動開根號)
手動開根還沒學會。。。主要是程式碼太迷了得研究下 要學手動開根的話可以參考一下連結: https://www.cnblogs.com/KasenBob/p/10041399.html 我是用了牛頓迭代法,可以參考以下內容: http://www.matrix67.com/blog/archives/3
Jacobi和Gauss-Seidel迭代法求解方程組
迭代法簡介 迭代法也稱輾轉法,是一種不斷用變數的舊值遞推新值的過程,跟迭代法相對應的是直接法(或者稱為一次解法),即一次性解決問題。迭代演算法是用計算機解決問題的一種基本方法,它利用計算機運算速度快、適合做重複性操作的特點,讓計算機對一組指令(或一定步驟)進行重複執行,在每次執行這組
C程式設計案例(牛頓迭代法求高次方程的根)
牛頓迭代法求方程的根 1. 牛頓迭代法的幾何解釋 註解: 設 r r
[數值分析]不動點迭代法求解非線性方程
Promble1 求出f(x)=3x2−ex=0f(x)=3x2−ex=0的根,精確到小數點後的第4位。 解 首先我們利用matlab繪圖確定出根的大致區域。 由圖可知存在三個有根區間[−1