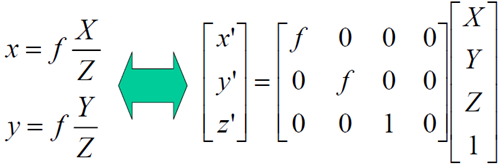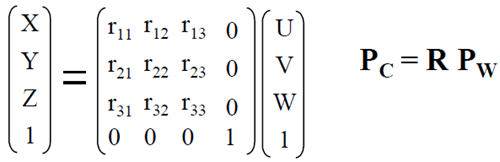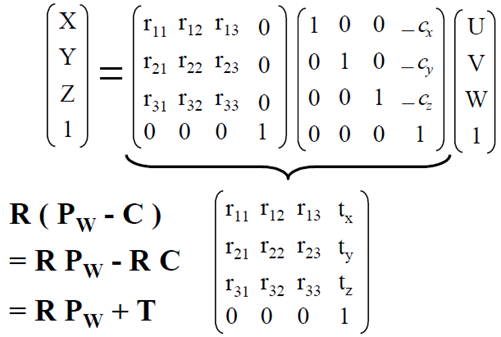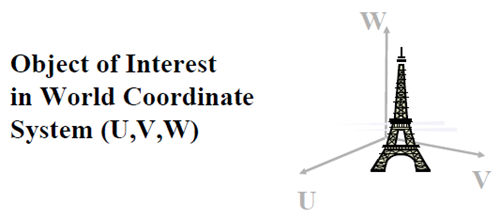
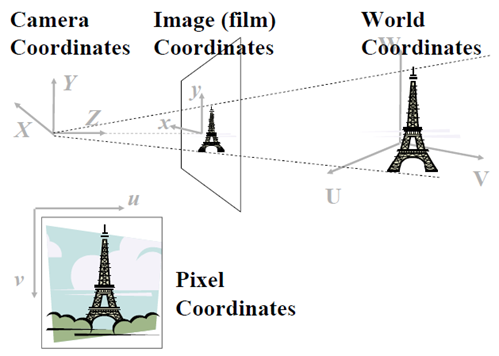
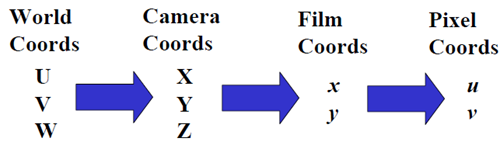
試想像一下，很多遊客同時在不同角度拍攝Eiffel Tower(埃菲爾鐵塔)，該如何用數學的方法來描述這一過程呢？首先要解決的問題就是定位，或者說座標選定的問題，埃菲爾鐵塔只有一座，如果按經、緯度來刻畫，它的座標是唯一確定的，但遊客顯然不關係這一點，他(她)只按自己的喜好選擇角度和位置，因此，物體(景物)有物體的座標系統，相機有相機的座標系統，即便同一個相機，當調整引數時，在同樣的位置、相同的角度，也可能得到不同的影象。為了統一描述，有必要引入世界座標(或物體座標)、相機座標和像平面座標。

世界座標用UVW記。

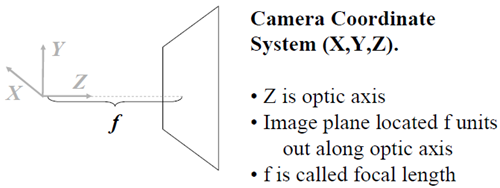
相機座標用XYZ記。中學物理告訴我們，物體與像是倒的關係，但作為數學分析，我們採用虛像。像平面用xoy記。

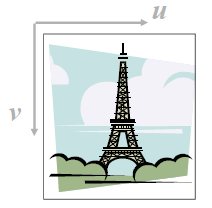
而數字影象用(u,v)來表示，不弄混淆像平面和數字影象這兩個概念，同一個像通過平移、拉伸等，可以得到不同的數學影象(u,v)。

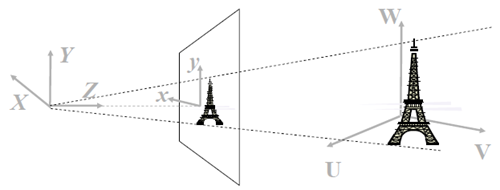
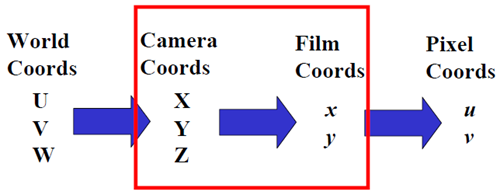
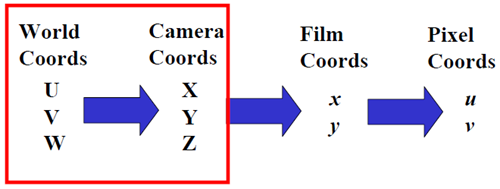
總體來看，就是

我們需要用數學的語言來描述這一過程。先看中間部分。

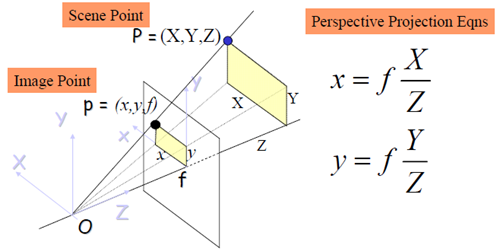
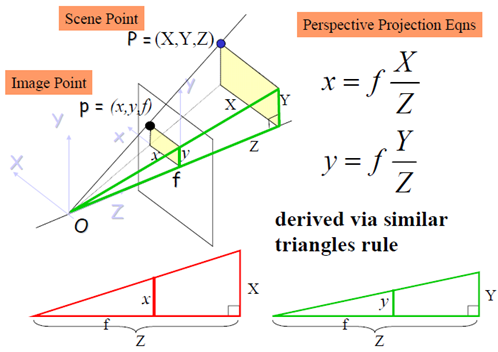
紅框標註的部分是3D物體到2D像平面的透視投影(如果不明白透視投影的概念，需要補一下高等幾何)

顯然，OP上的任一點的像都是p(x,y)，為了描述這一關係，需要引入齊次座標。

By convention, we specify that given (x’,y’,z’) we can recover the 2D point (x,y) as

x=\frac{x^'}{z^'}

Note: (x,y) = (x,y,1) = (2x, 2y, 2) = (k x, ky, k)

關於齊次座標，更詳細的介紹可參考高等幾何。

上述透視投影的過程可以描述為

正如開頭所言，不同遊客會選擇不同的位置和角度拍攝同一物體，因此，物體對於相機的關係各不相同，這就是物體到相機座標變換的問題。

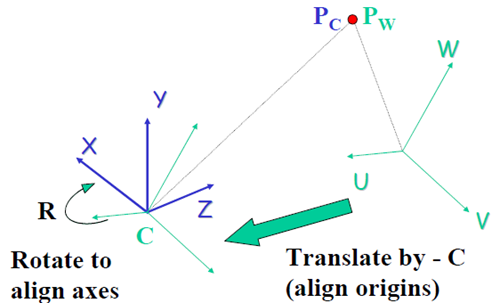
上述紅框部分描述的是從物體的座標(稱為世界座標)到相機座標變換的過程，它是一種剛體運動，可以用平移、旋轉來描述。

上圖表示的是從世界座標變換到相機座標：P

平移是容易理解的，我們先討論更簡單的情形，即假設世界座標系和相機座標系的原點重合，則變換隻剩下旋轉了。

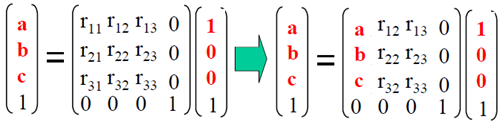
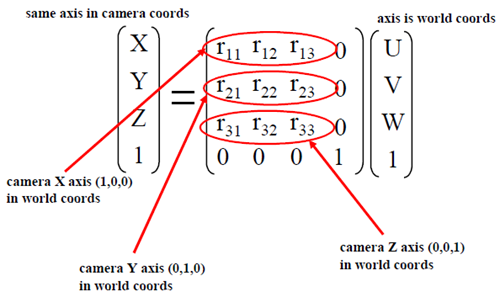
旋轉矩陣的元素也很容易確定。試想(U,V,W)=(1,0,0)，而它在相機座標系中的座標是(X,Y,Z)=(a,b,c)(同一物理點的不同座標)則有：

因此有：

由於該旋轉是剛體運動，因此它是正交變換，滿足R−1=RTR−1=RT，所以有：

不難得出：

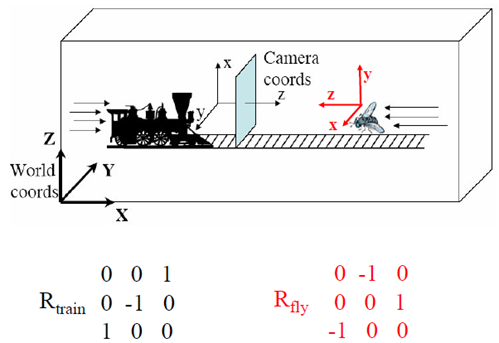
看一個例子：

由於物體的座標到相機座標的變換，相對於相機內部引數而言屬於外部引數(External Parameters)，往往寫作R和T，即

總結

本小節講述瞭如何將3D世界座標系中的點變換到相機座標系中，然後經透視投影，變成2D像平面上的點(x,y).

總結：這個比第一節要難理解些，設計到一些矩陣變換，三維到二維資訊的變換。