先思考一個問題：用兩個相機在不同的位置拍攝同一物體，如果兩張照片中的景物有重疊的部分，我們有理由相信，這兩張照片之間存在一定的對應關係，本節的任務就是如何描述它們之間的對應關係，描述工具是對極幾何 ，它是研究立體視覺的重要數學方法。

　　要尋找兩幅影象之間的對應關係，最直接的方法就是逐點匹配，如果加以一定的約束條件對極約束(epipolar constraint)，搜尋的範圍可以大大減小。

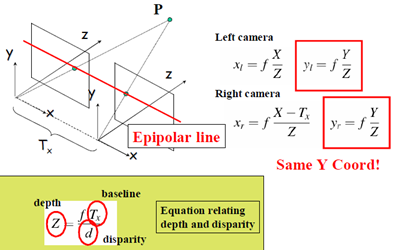
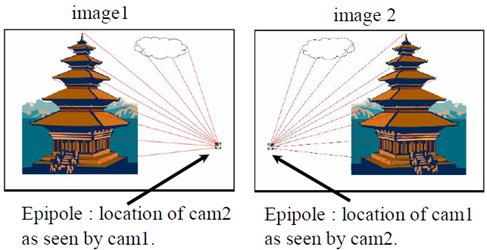
　　先回顧簡單的立體成像系統

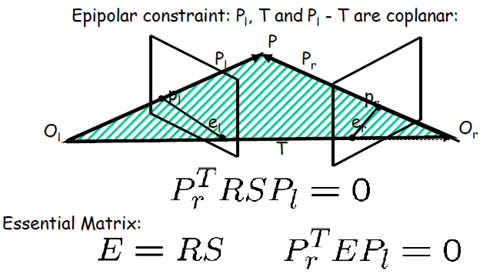
對極約束的圖示

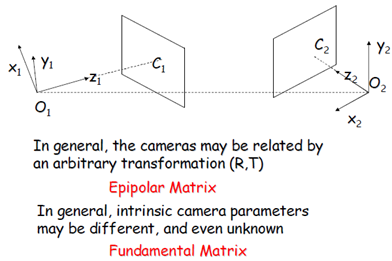
更一般的立體成像關係：兩個相機的座標無任何約束關係，相機的內部引數可能不同，甚至是未知的。要刻畫這種情況下的兩幅影象之間的對應關係，需要引入兩個重要的概念——對極矩陣(Epipolar Matrix)和基本矩陣(Fundamental Matrix)。

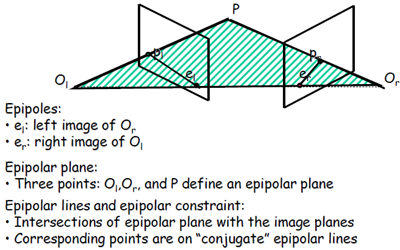
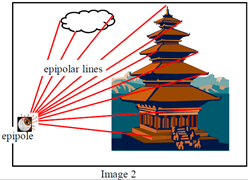
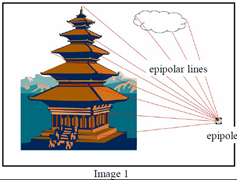
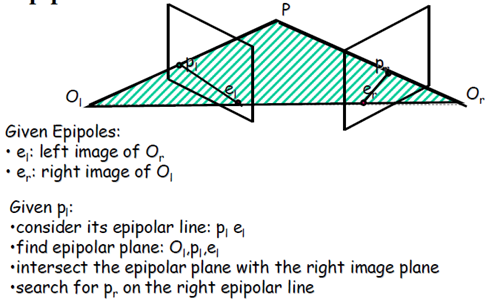
對極幾何中的重要概念（參考下圖）：

極點：極點elel:右相機座標原點在左像平面上的像；極點erer:左相機座標原點在右像平面上的像

極平面：由兩個相機座標原點OlOl、OrOr和物點P組成的平面

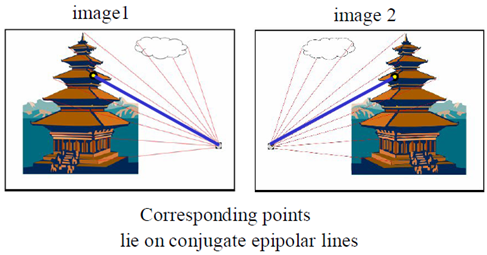
級線：極平面與兩個像平面的交線，即plelplel和prerprer

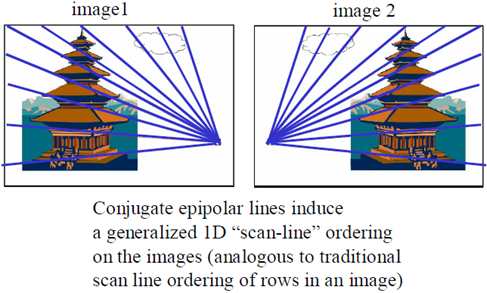
級線約束：兩極線上點的對應關係

有點煩人，先轉移一下話題：What would Pinhead’s eye look like close up?

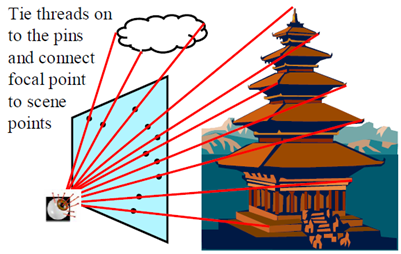
如果兩個人同時看這一景物，將是什麼樣的呢？

再回到對極幾何圖上來，通過上面幾幅圖示，利用對極幾何的約束關係，我們可以：

1. 找到物點P在左像平面上的像點plpl；

2. 畫出極線plelplel；

3. 找到極平面OlplelOlplel與右像平面的交線，即得極線prerprer；

4. 像點plpl的對應點一定在極一prerprer上。

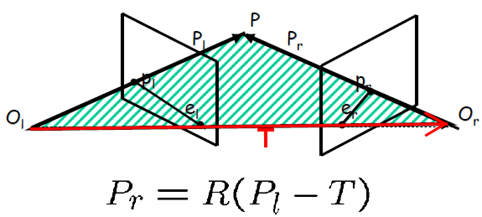
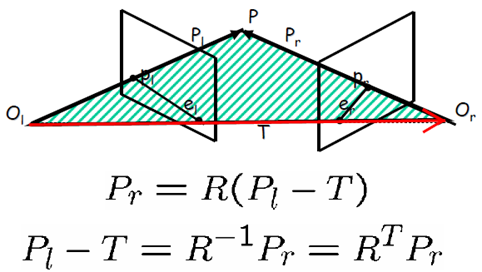
兩個相機座標系之間的關係為

由於R是正交矩陣，因此可寫為

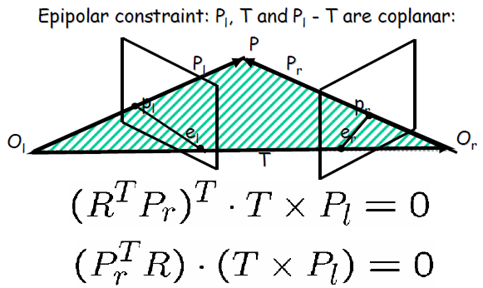
三向量共面，它們的混合積為零(混合積對應於有向體積)

將向量乘(叉乘)寫成矩陣的形式

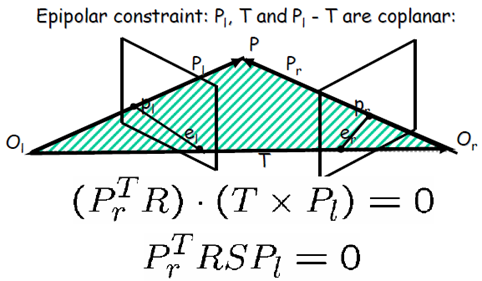
通過進一步的改寫，可以得到左像點和右像點之間約束關係(非常簡單、漂亮)

顯然，左像點plpl和右像點prpr是通過矩陣E=RSE=RS來約束的，我們稱矩陣EE為本質矩陣(Essential Matrix)，它的基本性質有：

• has rank 2(秩為2)

• depends only on the EXTRINSIC Parameters (R & T)(僅依賴於外部引數R和T)