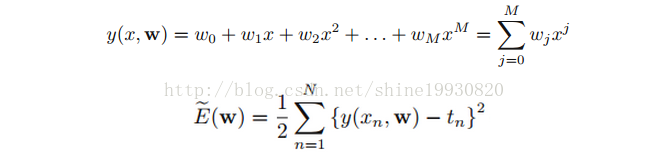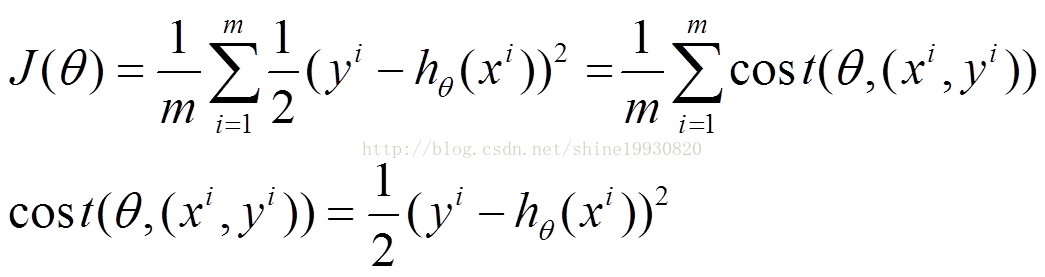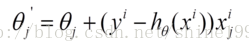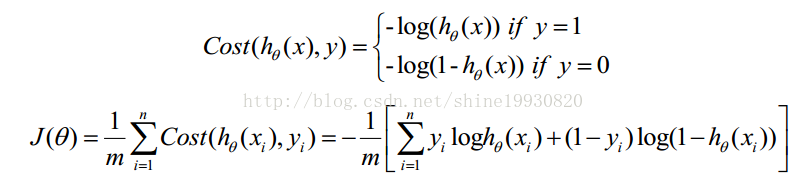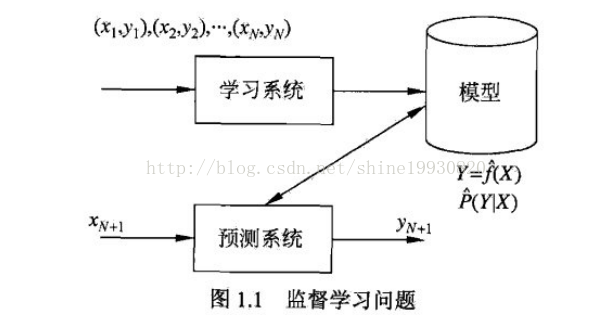
監督學習問題：

1、線性迴歸模型：

適用於自變數X和因變數Y為線性關係

2、廣義線性模型：

對於輸入空間一個區域改變會影響所有其他區域的問題，解決為：把輸入空間劃分成若干個區域，然後對每個區域用不同的多項式函式擬合

是為了克服線性迴歸模型的缺點出現的，是線性迴歸模型的推廣。

首先自變數可以是離散的，也可以是連續的。離散的可以是0-1變數，也可以是多種取值的變數。

與線性迴歸模型相比較，有以下推廣：

根據不同的資料，可以自由選擇不同的模型。大家比較熟悉的Logit模型就是使用Logit聯接、隨機誤差項服從二項分佈得到模型。

迴歸的線性模型

對於輸入空間一個區域改變會影響所有其他區域的問題，解決為：把輸入空間劃分成若干個區域，然後對每個區域用不同的多項式函式擬合

Polynomial Curve Fitting

為神馬不是差的絕對值？請看下面分解：

當我們尋找模型來擬合數據時，偏差是不可避免的存在的。對一個擬合良好的模型而言，這個偏差整體應該是符合正態分佈的，

根據貝葉斯定理：P(h|D)=P(D|h)*P(h)/P(D)     即P(h|D)∝P(D|h)*P(h) (∝表示“正比於”)
    結合前面正態分佈，我們可以寫出這樣的式子：實際縱座標為 Yi 的點 (Xi, Yi) 發生的概率 p(di|h)∝exp(-(ΔYi)^2)

各個資料點偏差是獨立的，所以可以把每個概率乘起來。於是生成 N 個數據點的概率為 EXP[-(ΔY1)^2] * EXP[-(ΔY2)^2] * EXP[-(ΔY3)^2] * .. = EXP{-[(ΔY1)^2 + (ΔY2)^2 + (ΔY3)^2 + ..]} 最大化這個概率就是要最小化 (ΔY1)^2 + (ΔY2)^2 + (ΔY3)^2 + .. 。得解！
正態分佈的概率密度函式是尤拉數的冪函式形式。並不是所有的模型都可以有最優解，有些只有區域性最優，有些則壓根找不到，例如NPC問題。絕對值的和無法轉化為一個可解的尋優問題，既然無法尋優如何得到恰當的引數估計呢？

x(i)的估計值與真實值y(i)差的平方和作為錯誤估計函式，前面乘上的1/2是為了在求導的時候，這個係數就不見了。如何調整θ以使得J(θ)取得最小值有很多方法：

1. 梯度減少的過程：

對於我們的函式J(θ)求偏導J：

下面是更新的過程，也就是θi會向著梯度最小的方向進行減少。θi表示更新之前的值，-後面的部分表示按梯度方向減少的量，α表示步長，也就是每次按照梯度減少的方向變化多少。

對於一個向量θ，每一維分量θi都可以求出一個梯度的方向，我們就可以找到一個整體的方向，在變化的時候，我們就朝著下降最多的方向進行變化就可以達到一個最小點，不管它是區域性的還是全域性的。

梯度下降法是按下面的流程進行的：

1）首先對x 賦值，這個值可以是隨機的，也可以讓x是一個全零的向量。

2）改變x 的值，使得f(x)按梯度下降的方向進行減少。

3）迴圈迭代步驟2，直到x的值變化到使得f(x)在兩次迭代之間的差值足夠小，比如0.00000001，也就是說，直到兩次迭代計算出來的f(x)基本沒有變化，則說明此時f(x)已經達到區域性最小值了。

• 靠近極小值時收斂速度減慢。
• 直線搜尋時可能會產生一些問題。
• 可能會“之字形”地下降。

• 這個演算法將會在很大的程度上被初始點的選擇影響而陷入區域性最小點

1、批量梯度下降的求解思路如下：

（1）將J(theta)對theta求偏導，得到每個theta對應的的梯度

   

（2）由於是要最小化風險函式，所以按每個引數theta的梯度負方向，來更新每個theta

（3）從上面公式可以注意到，它得到的是一個全域性最優解，但是每迭代一步，都要用到訓練集所有的資料，如果m很大，那麼可想而知這種方法的迭代速度！！所以，這就引入了另外一種方法，隨機梯度下降。

2、隨機梯度下降的求解思路如下：

（1）上面的風險函式可以寫成如下這種形式，損失函式對應的是訓練集中每個樣本的粒度，而上面批量梯度下降對應的是所有的訓練樣本：

（2）每個樣本的損失函式，對theta求偏導得到對應梯度，來更新theta

（3）隨機梯度下降是通過每個樣本來迭代更新一次，如果樣本量很大的情況（例如幾十萬），那麼可能只用其中幾萬條或者幾千條的樣本，就已經將theta迭代到最優解了，對比上面的批量梯度下降，迭代一次需要用到十幾萬訓練樣本，一次迭代不可能最優，如果迭代10次的話就需要遍歷訓練樣本10次。但是，SGD伴隨的一個問題是噪音較BGD要多，使得SGD並不是每次迭代都向著整體最優化方向。

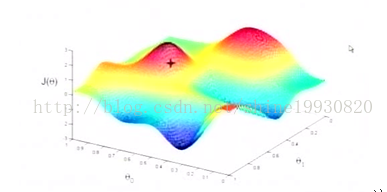
對於上面的linear regression問題，最優化問題對theta的分佈是unimodal，即從圖形上面看只有一個peak，所以梯度下降最終求得的是全域性最優解。然而對於multimodal的問題，因為存在多個peak值，很有可能梯度下降的最終結果是區域性最優。

一個衡量錯誤的指標是root mean square error：


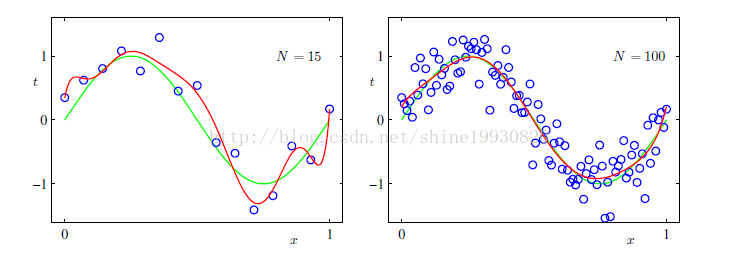
過擬合的解決辦法，目前講了三點：

1. 增加訓練資料集合
2. 加入本書的"萬金油" 貝葉斯方法
3. 加入regularization。

Regularization

control the over-fitting phenomenon

引數w對訓練資料的變化異常敏感，儘可能的去捕捉這個變化(使誤差最小)，而他捕捉的方式，就是肆意改變自身的大小，而不管訓練資料的大小(向量w的各個值會正負抵消，而得出一個和目標變數相當的輸出)。這是模型的缺陷，也是過擬合的元凶。 而引入正則化項之後，向量w想要變大自身並正負抵消來擬合目標時，|w|會變的非常大，與目標變數相去甚遠，過擬合的陰謀失敗了。

Ordinary Least Squares

fits a linear model with coefficientsWto minimize the residual sum of squares between the observed responses in the dataset, and the responses predicted by the linear approximation. Mathematically it solves a problem of the form:

However, coefficient estimates for Ordinary Least Squares rely on the independence of the model terms.

Ordinary Least Squares Complexity

X is a matrix of size (n, p) this method has a cost of, assuming that n>=p.

 Ridge Regression 嶺迴歸

regression addresses some of the problems ofOrdinary Least Squaresby imposing a penalty on the size of coefficients. The ridge coefficients minimize a penalized residual sum of squares,

Here,is a complexity parameter that controls the amount of shrinkage: the larger the value of, the greater the amount of shrinkage and thus the coefficients become more robust to collinearity.

引數值和alpha的變化關係。

ax.set_color_cycle(['b','r','g','c','k','y','m'])

Bayesian Regression

最大似然估計中很難決定模型的複雜程度，ridge迴歸加入的懲罰引數其實也是解決這個問題的，同時可以採用的方法還有對資料進行正規化處理，另一個可以解決此問題的方法就是採用貝葉斯方法。 目標變數t的取值是由一個deterministic function y(x,w)和一個高斯噪聲共同決定的，如3.7式：
目標值t的概率分佈可以寫成3.8： 
這裡的x是向量，是一個更普適的表達。式3.8的含義是，t取某個值的概率，是均值為y(x,w)，precision為beta的正態分佈。 選擇二階損失函式，t的預測就是條件數學期望 E(t|x):  高斯噪聲沒有了。 以上，敲定了本問題的概率模型，接下來給出似然函式並用最大似然求解。 用X表示所有的向量x, X={x1....xN}，他們分別對應向量t的t1....tN，在觀測點獨立同分布的前提下，式3.8可以對所有向量t和向量x寫成 ：
    這就是likelihood function，後續還會經常用到。與前面一樣，我們最大化這個似然函式：對這個式子兩邊求ln，然後令x偏導數為0，求得拐點的位置，也就求得了w的表示式。     與普通的線性迴歸比較，likelyhood function p(t|x,w)是一致的。不同的是：引數w，一個是確定的，一個是概率分佈；對最終結果t的預測，一個是通過損失函式來決定，一個是在w的空間上積分。 高斯噪聲假設下，p(t|x)是unimodal(單峰，有一個極大值)的，這可能與事實不符。而混合條件高斯分佈，它會允許multimodal。 貝葉斯迴歸方法有三個關鍵點： 1. 求概率分佈p(W|D).  2. 求likelyhood p(t|x,W) .  3. 在w空間上積分(1.68)。 在我們未觀測到資料集D之前，可以先假設w服從均值為m0，方差為S0的高斯分佈：

w的後驗概率與似然函式和先驗概率的乘積成正比。因為w的先驗概率是高斯分佈，所以共軛的後驗概率也是高斯分佈(高斯likelyhood=>高斯先驗w=>高斯後驗w)。 已知資料x和t， w的後驗概率為3.49：

Phi 自變數x的特徵組成的矩陣。
w的先驗在負無窮正無窮上均勻分佈時，貝葉斯線性迴歸就蛻化成了普通的線性迴歸。普通線性迴歸並不認識w是一個概率分佈，就是在所有的可能性下，直接求解似然函式。
對於先驗概率的選擇，有更加泛化的表示，如公式3.56。為了簡化問題，我們看一個w先驗概率為： 均值為0，方差為alpha倒數的高斯分佈：
看這兩個式子，Phi和T都來自觀測資料，待定引數只有alpha和beta。
把這個後驗分佈寫成具體的概率密度函式，然後對它的w求log，就得到了

相似於λ = α/β 時的ridge regression

貝葉斯視角下的模型選擇

對於一個問題、一個數據集，可能會有多個模型與之對應，每個模型都會以一定概率生成這個資料集，那麼我們選擇哪一個模型呢？按照以前的做法，我可能會說選擇概率最大的那個唄。
如果我們有一個數據集D,有L個模型 Mi，i=1,....L，我們感興趣的是給定資料D，選擇某個Mi的後驗概率如3.66: 給定x，對於t的預測可以用3.67來表示：

Logistic regression

Logistic迴歸與多重線性迴歸實際上有很多相同之處，最大的區別就在於它們的因變數不同，可以歸於同一個家族，即廣義線性模型（generalizedlinear model）。 如果是連續的，就是多重線性迴歸；如果是二項分佈，就是Logistic迴歸；如果是Poisson分佈，就是Poisson迴歸；如果是負二項分佈，就是負二項迴歸。 Logistic迴歸主要在流行病學中應用較多，比較常用的情形是探索某疾病的危險因素，根據危險因素預測某疾病發生的概率，等等。例如，想探討胃癌發生的危險因素，可以選擇兩組人群，一組是胃癌組，一組是非胃癌組，兩組人群肯定有不同的體徵和生活方式等。這裡的因變數就是是否胃癌，即“是”或“否”，自變數就可以包括很多了，例如年齡、性別、飲食習慣、幽門螺桿菌感染等。自變數既可以是連續的，也可以是分類的。

常規步驟

Regression問題的常規步驟為：

1. 尋找h函式（即hypothesis）；
2. 構造J函式（損失函式）；
3. 想辦法使得J函式最小並求得迴歸引數（θ）

構造預測函式h
Logistic迴歸雖然名字裡帶“迴歸”，但是它實際上是一種分類方法，主要用於兩分類問題（即輸出只有兩種，分別代表兩個類別），所以利用了Logistic函式（或稱為Sigmoid函式），函式形式為：
Sigmoid 函式在有個很漂亮的“S”形;
決策邊界分為線性和非線性. 對於線性邊界的情況:

構造損失函式J

Cost函式和J函式如下，它們是基於最大似然估計推導得到的。

下面詳細說明推導的過程：

相關推薦