概率論:常見概率分佈
常見離散概率分佈
Bernoulli、Binomial、Poisson
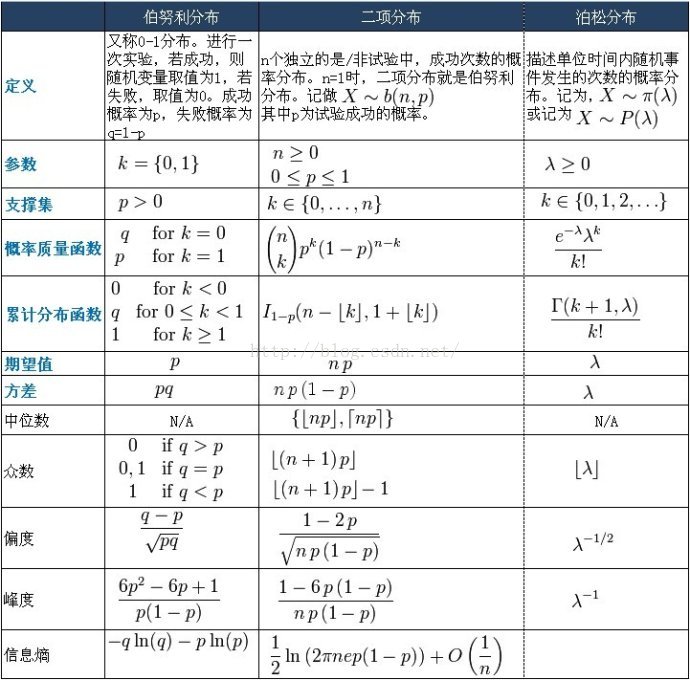
伯努利分佈
對單次拋硬幣的建模,X~Bernoulli(p)的PDF為
隨機變數X只能取{0, 1}。
對於所有的pdf,都要歸一化!而對於伯努利分佈,已經天然歸一化了,因此歸一化引數就是1。
現在我們假設我們有一個 x 的觀測值的資料集 D = {x 1 , . . . , x N } 。假設每次觀測都是獨立地從 p(x | μ) 中抽取的,因此我們可以構造關於 μ 的似然函式如下
mle得出 μ = m/N。
二項分佈
很多次拋硬幣的建模就是二項分佈了。二項分佈是n次獨立的伯努利試驗的和(故根據中心極限定理可知,二項分佈的極限分佈為高斯分佈)。它的期望值和方差分別等於每次單獨試驗的期望值和方差的和。
注意二項分佈有兩個引數,n和p,要考慮拋的次數。
二項分佈的取值X一般是出現正面的次數,其PDF為:
2.10就是二項分佈pdf的歸一化引數。
mle式2.9亦得出μ = m/N,故式 2.5和式2.9是等價的。lz:二項分佈相當於是通過伯努利分佈直接構造出的似然函式(沒有歸一化)的歸一化分佈。
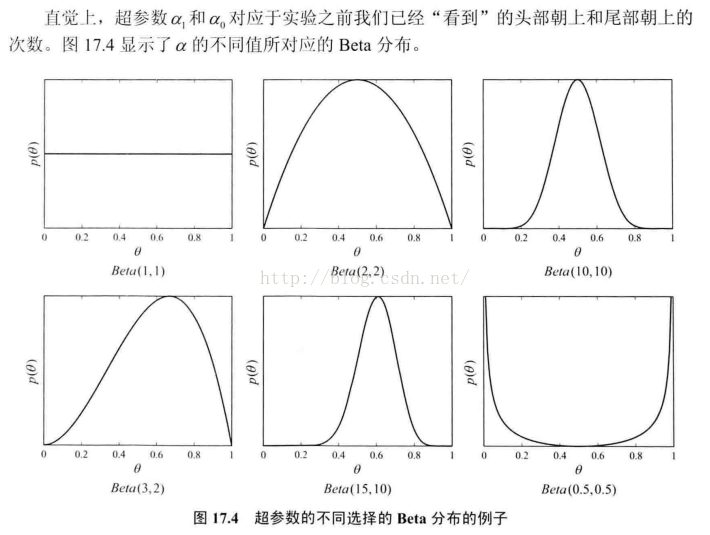
beta分佈
如果是beta分佈,把歸一化項換成beta函式分之一即可,這樣可以從整數情況推廣為實數情況。所以beta分佈是二項分佈的實數推廣!
多項式分佈Multinomial
多項分佈則更進一層,拋硬幣時X只能有兩種取值,當X有多種取值時,就應該用多項分佈建模。
這時引數p變成了一個向量p⃗ =(p1,…,pk)表示每一個取值被選中的概率,那麼X~Multinomial(n,p)的PDF為:
二元變數可以用來描述只能取兩種可能值中的某一種這樣的量。然而,我們經常會遇到可以取 K 個互斥狀態中的某一種的離散變數。雖然有多種方式來表達這種變數,但是我們稍後會看到,一種比較方便的表示方法是“1- of - K ”表示法。這種表示方法中,變數被表示成一個 K 維向量 x ,向量中的一個元素 x k 等於1,剩餘的元素等於0。例如,如果我們有一個能夠取 K = 6 種狀態的變數,這個變數的某次特定的觀測恰好對應於 x 3 = 1 的狀態,那麼 x 就可以表示為x = (0, 0, 1, 0, 0, 0) T。注意,這樣的向量滿足∑ xk=1
我們可以考慮 m 1 , . . . , m K 在引數 μ 和觀測總數 N 條件下的聯合分佈。根據似然函式,這個分佈的形式為
歸 一 化 系 數 是 把 N 個 物 體 分 成 大 小為 m 1 , . . . , m K 的 K 組的方案總數,定義為
注意, m k 滿足下面的限制
或者通過概率直接推出
常見連續概率分佈
常見的概率分佈_文庫下載http://www.wenkuxiazai.com/doc/e14db3d233d4b14e852468c0.html
常見的概率分佈_文庫下載http://www.wenkuxiazai.com/doc/e14db3d233d4b14e852468c0.html
常見的連續分佈的概率密度函式和累積分佈度函式:
均勻分佈
指數分佈
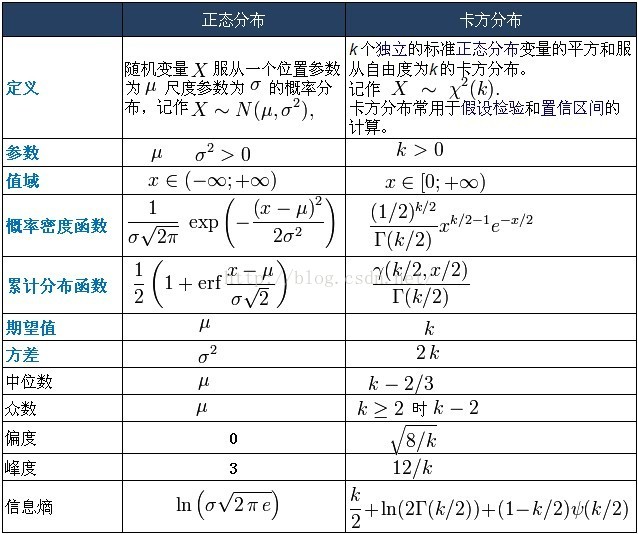
正態分佈與卡方分佈
Beta分佈
拉普拉斯分佈 Laplace Dist
在概率論與統計學中,拉普拉斯分佈是以皮埃爾-西蒙·拉普拉斯的名字命名的一種連續概率分佈。由於它可以看作是兩個不同位置的指數分佈背靠背拼接在一起,所以它也叫作雙指數分佈。當資料分佈的波峰比正態分佈更尖銳時使用 Laplace 分佈。例如,Laplace 分佈用於生物、金融和經濟學方面的建模。
兩個相互獨立同概率分佈指數隨機變數之間的差別是按照指數分佈的隨機時間布朗運動,所以它遵循拉普拉斯分佈。
概率密度函式 累積分佈函式概率分佈、概率密度以及分位數函式
如果隨機變數的概率密度函式分佈為
那麼它就是拉普拉斯分佈。其中,μ 是位置引數,b > 0 是尺度引數。如果 μ = 0,那麼,正半部分恰好是尺度為 1/2 的指數分佈。
拉普拉斯分佈的概率密度函式讓我們聯想到正態分佈,但是,正態分佈是用相對於 μ 平均值的差的平方來表示,而拉普拉斯概率密度用相對於平均值的差的絕對值來表示。因此,拉普拉斯分佈的尾部比正態分佈更加平坦。
根據絕對值函式,如果將一個拉普拉斯分佈分成兩個對稱的情形,那麼很容易對拉普拉斯分佈進行積分。它的累積分佈函式為:
 |  |
![= \left\{\begin{matrix} &\frac12 \exp \left( -\frac{\mu-x}{b} \right) & \mbox{if }x < \mu \\[8pt] 1-\!\!\!\!&\frac12 \exp \left( -\frac{x-\mu}{b} \right) & \mbox{if }x \geq \mu \end{matrix}\right.](https://wikimedia.org/api/rest_v1/media/math/render/svg/c403da990d5c1bd5c8147f9821c465afc744ff97) | |
![=0.5\,[1 + \sgn(x-\mu)\,(1-\exp(-|x-\mu|/b))]](https://wikimedia.org/api/rest_v1/media/math/render/svg/d88a06d233cba19a43a8d9ba11894acdc28354fd) |
逆累積分佈函式為
拉普拉斯分佈的數字特徵
| 引數 |  位置引數(實數) 位置引數(實數) 尺度引數(實數) 尺度引數(實數) |
|---|---|
| 支撐集 |  |
| 概率密度函式 |  |
| 期望值 |  |
| 中位數 |  |
| 眾數 |  |
| 方差 |  |
| 偏度 |  |
| 峰度 |  |
| 資訊熵 |  |
| 動差生成函式 |  for for  |
| 特性函式 |  |
拉普拉斯分佈的性質
- 如果
並且
,則
是指數分佈。
- 如果
與
,則
。
Gaussian-Exponential Mixture
laplace分佈可以看成是高斯分佈和指數分佈的混合體。
ref: [PRML]

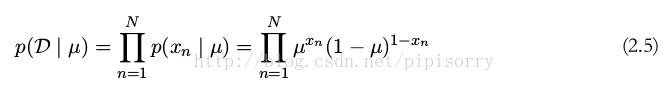
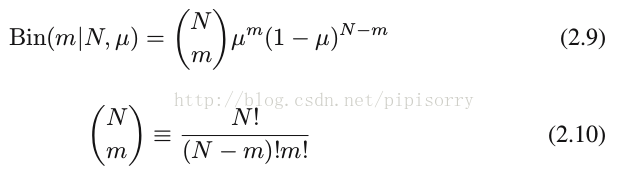












![= \frac{1}{2b} \left\{\begin{matrix} \exp \left( -\frac{\mu-x}{b} \right) & \mbox{if }x < \mu \\[8pt] \exp \left( -\frac{x-\mu}{b} \right) & \mbox{if }x \geq \mu \end{matrix}\right.](https://wikimedia.org/api/rest_v1/media/math/render/svg/4af44a4a16a26cd390e42188ad06c5d23e9d6a73)
