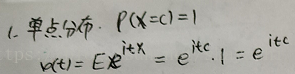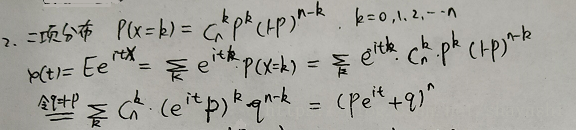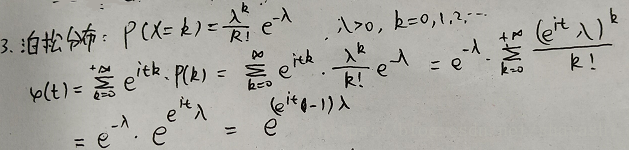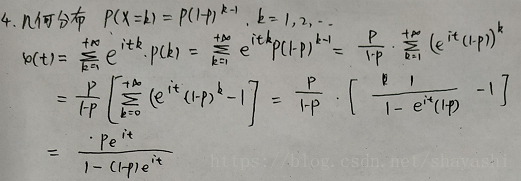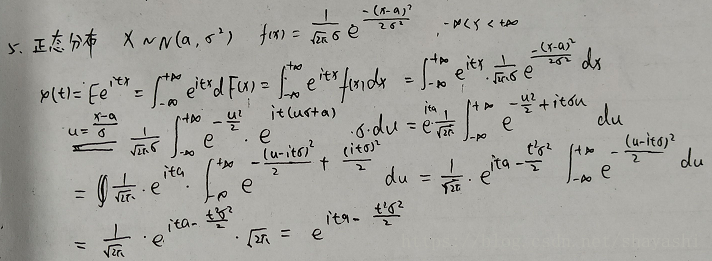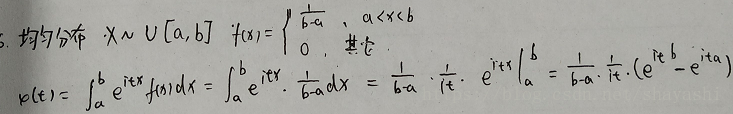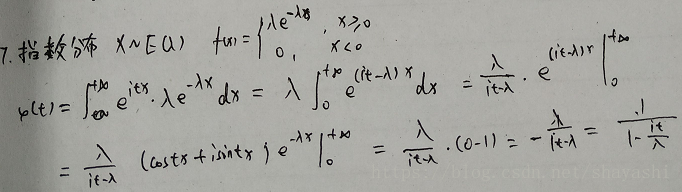常見概率分佈的特徵函式推導
特徵函式定義是:設X是實值隨機變數,則對任意實數t,有
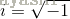
一、離散概率分佈
1.單點分佈
單點分佈的分佈列為
其特徵函式計算方法如下:
2.二項分佈
二項分佈的分佈列為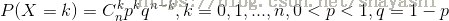
其特徵函式的計算方法如下:
3.泊松分佈
泊松分佈的分佈列為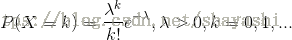
其特徵函式的計算方法如下:
4.幾何分佈
幾何分佈的分佈列為
特徵函式的計算方法如下:
二、連續概率分佈
1.正態分佈
正態分佈的分佈密度是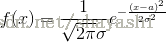
特徵函式推導過程如下:
2.均勻分佈
均勻分佈的分佈密度是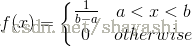
特徵函式推導過程如下:
3.指數分佈
指數分佈的分佈密度是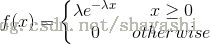
特徵函式推導過程如下:
相關推薦
常見概率分佈的特徵函式推導
特徵函式定義是:設X是實值隨機變數,則對任意實數t,有 稱為隨機變數X的特徵函式,其中。 一、離散概率分佈 1.單點分佈 單點分佈的分佈列為。 其特徵函式計算方法如下: 2.二項分佈 二項分佈的分佈列為。 其特徵函式的計算方法如下: 3.泊松分佈 泊松分佈的
第3章 概率 第4章 常見概率分佈
一個樣本點是試驗中最基本的結果 組合法則(Nn)=N!/(n!(N-n)!) 事件的補集是指事件所有的不發生樣本點Ac 概率的加法:p(AUB)=p(A)+p(B)-p(AnB) 互斥事件:p(AUB)=p(A)+p(B) 條件概率:p(A|
常見概率分佈總結
Discrete Bernoulli distribution pmf fX(x)=P(X=x)={(1−p)1−xpxfor x = 0 or 10otherwisef_X(x) = P(X=
scipy.stats的用法——常見的分佈和函式
介紹python統計函式庫scipy.stats中常見的分佈和函式 #commom distributions: ''' uniform,norm,poisson,bernoulli,expon,lognorm norm,t,chi2,f ''' #commom
概率論:常見概率分佈
常見離散概率分佈Bernoulli、Binomial、Poisson伯努利分佈對單次拋硬幣的建模,X~Bernoulli(p)的PDF為隨機變數X只能取{0, 1}。對於所有的pdf,都要歸一化!而對於伯努利分佈,已經天然歸一化了,因此歸一化引數就是1。現在我們假設我們有一個
【Derivation】MarkDown Letex編碼 之 正態分佈特徵函式證明
**求證:$\varphi(u)=e^{jau-\frac{1}{2}u^2\sigma^2} \ \ \ , t\in R $** **證:** * * $$\varphi(u)=\i
【Derivation】正態分佈特徵函式證明-X~N(a,sigma^2)
求證:φ(u)=ejau−12u2σ2,t∈R 證: φ(u)=∫+∞−∞ejuxf(x)dx =∫+∞−∞ejux12πσ2−−−−√e−(x−a)22σ2dx 整理,得: φ(u)=12π
資料科學家應知必會的6種常見概率分佈
前言 假設你是個大學老師。 在檢查了一週的作業後,對學生進行了打分。 讓錄分員建立一個包含所有學生成績的電子表格,要求是隻含分數不含學生姓名等資訊。 於是乎,錄分員一個大粗心,漏錄了好幾個分數,介個時候不知道把誰給漏錄了。來看看怎麼解決這個
常用概率分佈函式及隨機特徵
常見分佈的隨機特徵離散隨機變數分佈伯努利分佈(二點分佈)伯努利分佈亦稱“零一分佈”、“兩點分佈”。稱隨機變數X有伯努利分佈, 引數為p(0<p<1),如果它分別以概率p和1-p取1和0為值。EX= p,DX=p(1-p)。伯努利試驗成功的次數服從伯努利分佈,引數p
Matlab統計工具箱中各類概率分佈函式使用方法介紹
1. Matlab Statistics Toolbox 中概率分佈函式介紹 Matlab Statistics Toolbox 提供了對幾乎所有概率分佈的支援,可以方便產生服從各類分佈的隨機數及其PDF/CDF 函式。
常見的幾種概率分佈
文章來源:http://blog.csdn.net/pipisorry/article/details/39076957 常見離散概率分佈 Bernoulli、Binomial、Poisson Note: 一般的二項分佈是n次獨立的伯努利試驗的和。它的期望值和方
概率分佈函式--二項分佈&poisson分佈
import matplotlib.pyplot as plt import numpy as np 課程要求畫圖,檢視官方文件 numpy.random.binomial(n, p, size=None) n trials and p probabili
3 概率分佈與隨機函式
更多MATLAB資料分析視訊請點選,或者在網易雲課堂上搜索《MATLAB資料分析與統計》 http://study.163.com/course/courseMain.htm?courseId=1003615016 隨著計算機技術的快速發展,隨機數在越來越多的領域得
一分鐘瞭解“matlab產生某個概率分佈的概率密度函式”
網上或者matlab文件裡查詢pdf函式,幾乎所有能遇到的概率密度函式都會在裡面遇到。 語法: y = pdf('name',x,A) y = pdf('name',x,A,B) y = pdf('name',x,A,B,C) y = pdf('name',x,A,
Excel在統計分析中的應用—第六章—概率分佈及概率分佈圖-Part5-泊松分佈函式POISSON.DIST()的應用
泊松分佈這種概率分佈型別經常看到,比較重要,必須掌握。 “當一個隨機事件,例如某電話交換臺收到的呼叫、來到某公共汽車站的乘客、某放射性物質發射出的粒子、顯微鏡下某區域中的白血球等等,以固定的平均瞬時速率λ(或稱密度)隨機且獨立地出現時,那麼這個事件在單位時間(面積或體積)內
概率函式,概率密度函式,概率分佈函式,高斯分佈
數學基礎複習之概率論(大部分來自百度百科和課本內容) 1.概率函式: (百度說的概率函式一般指概率分佈函式,但課件裡邊提到概率函式時是如下意思↓) 離散型隨機變數的分佈的表現形式 注:截圖來自同濟大學概率論與數理統計課件 2.概率密度函式: 在數學中,連續型隨機變數的概率
概率分佈和概率分佈函式
今天在面試小米演算法工程師的時候,遇到這麼一個面試問題,給定一個x取值範圍屬於[a,b],它的概率密度函式為f(x),求如何生成一系列隨機數,滿足這個概率分佈。這個問題首先要明白概率密度函式表達的是什麼意思先說均勻分佈: 均勻分佈的概率密度函式:f(x)=1/(b-a) 直接:np.random.
常見的離散型和連續型隨機變數的概率分佈
目錄 1 基本概念 4 參考文獻 1 基本概念 在之前的博文中,已經明白了概率分佈函式和概率密度函式。下面來講解一下常見的離散型和連續型隨機變數概率分佈。 在此之前,介紹幾個基本概念: 均值(期望值exp
隨機變數概率分佈函式彙總-離散型分佈+連續型分佈
2018.08.18-更新 概率分佈用以表達隨機變數取值的概率規律,根據隨機變數所屬型別的不同,概率分佈取不同的表現形式 離散型分佈:二項分佈、多項分佈、伯努利分佈、泊松分佈 連續型分佈:均勻分佈、正態分佈、指數分佈、伽瑪分佈、偏態分佈、貝塔分佈、威布林分佈、卡方分佈、
常見的概率分佈模型
這一陣子一直在做自己第一個真正意義的app專案,獨立完成,感覺壓力還是挺大的,很多知識點都不清晰,軟體的架構也很有問題,有很多東西都需要整理和記憶,所以決定做一下記錄。 其次,最近的科研專案壓力也比較大,很多之前學過的東西都忘記了,需要在部落格中記錄,所以下決