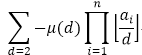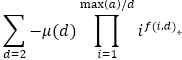解題報告:HDU_6053 TrickGCD 莫比烏斯反演
阿新 • • 發佈:2019-01-03
題意:
給一個長度為n的陣列A,讓你構造等長的陣列B,B陣列中的元素取值為小於等於A陣列中對應位置的元素,現在詢問B陣列中的gcd大於等於2的方案數
思路:(已更新容斥部分)
我們令g(d)為gcd為d的倍數的答案,那麼
所以根據容斥原理最後我們要求的答案為g(2)+g(3)+g(5)-g(6)+g(7)-g(10)+g(11)+g(13)-g(14)+g(15).....
即:
轉換一下:
f ( i , d ) 為 [ a / d ] = i 的A陣列中的元素個數,用一個字首和陣列維護就好
加上快速冪,那麼複雜度就降到了O( n log(n)^2 ) 了
程式碼:
#include<bits/stdc++.h> const long long mod = 1e9+7; using namespace std; const int N = 1e5+10; vector<int>pr; int mu[N]; bool Np[N]; inline void init(){ mu[1] = 1; for(int i=2;i<N;i++){ if(!Np[i]){ pr.emplace_back(i); mu[i]=-1; } for(int j=0,k=pr[j]*i;k<N;k=pr[++j]*i){ Np[k] = true; if(i%pr[j]==0){ mu[k] = 0; break; }mu[k] = -mu[i]; } } } int n,ed,mi; int A[N]; long long fro[N]; long long qpow(long long x,long long y){ if(x<=1)return 1; long long res = 1; while(y){ if(y&1)res=res*x%mod; y>>=1; x = x * x %mod; }return res; } long long work(){ for(int i=2;i<=ed;i++){ A[i]+=A[i-1]; }long long res = 0; for(int i=2;i<=mi;i++)if(mu[i]){ long long cnt = -mu[i]; int m = ed / i ; for(int j=1;j<=m;j++){ int l = i * j, r = min( ed , i * j + i - 1 ); cnt = cnt * qpow( j , A[r]-A[l-1] ) % mod; }res += cnt; } return ( res % mod + mod ) % mod; } int main() { init(); int T,cas=0; scanf("%d",&T); while(T--){ ed = 0;mi = 1e5; memset(A,0,sizeof(A)); scanf("%d",&n); for(int i=0,x;i<n;i++){ scanf("%d",&x); ed = max(ed,x); mi = min(mi,x); A[x]++; }printf("Case #%d: %I64d\n",++cas,work()); }return 0; }