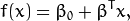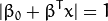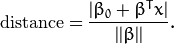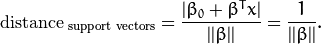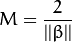什麼是支援向量機(SVM)?

支援向量機 (SVM) 是一個類分類器，正式的定義是一個能夠將不同類樣本在樣本空間分隔的超平面。 換句話說，給定一些標記(label)好的訓練樣本 (監督式學習), SVM演算法輸出一個最優化的分隔超平面。

如何來界定一個超平面是不是最優的呢? 考慮如下問題：

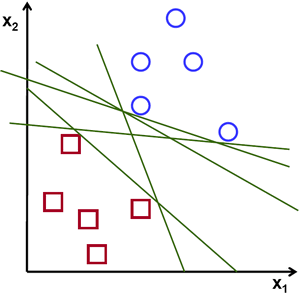
假設給定一些分屬於兩類的2維點，這些點可以通過直線分割， 我們要找到一條最優的分割線.

Note

 

在這個示例中，我們考慮卡迪爾平面內的點與線，而不是高維的向量與超平面。 這一簡化是為了讓我們以更加直覺的方式建立起對SVM概念的理解， 但是其基本的原理同樣適用於更高維的樣本分類情形。

在上面的圖中， 你可以直覺的觀察到有多種可能的直線可以將樣本分開。 那是不是某條直線比其他的更加合適呢? 我們可以憑直覺來定義一條評價直線好壞的標準:

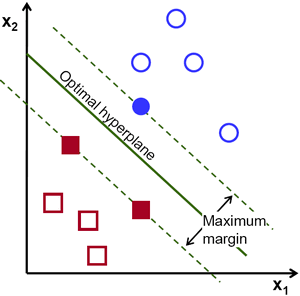
距離樣本太近的直線不是最優的，因為這樣的直線對噪聲敏感度高，泛化性較差。 因此我們的目標是找到一條直線，離所有點的距離最遠。

由此， SVM演算法的實質是找出一個能夠將某個值最大化的超平面，這個值就是超平面離所有訓練樣本的最小距離。這個最小距離用SVM術語來說叫做 間隔(margin) 。 概括一下，最優分割超平面 最大化 訓練資料的間隔。

如何計算最優超平面?

下面的公式定義了超平面的表示式:

 叫做 權重向量 ，  叫做 偏置(bias) 。

See also

 

關於超平面的更加詳細的說明可以參考T. Hastie, R. Tibshirani 和 J. H. Friedman的書籍 Elements of Statistical Learning

 ， section 4.5 (Seperating Hyperplanes)。

最優超平面可以有無數種表達方式，即通過任意的縮放  和  。 習慣上我們使用以下方式來表達最優超平面

式中  表示離超平面最近的那些點。 這些點被稱為 支援向量**。 該超平面也稱為 **canonical 超平面.

通過幾何學的知識，我們知道點  到超平面  的距離為:

特別的，對於 canonical 超平面, 表示式中的分子為1，因此支援向量到canonical 超平面的距離是

剛才我們介紹了間隔(margin),這裡表示為 , 它的取值是最近距離的2倍:

最後最大化  轉化為在附加限制條件下最小化函式  。 限制條件隱含超平面將所有訓練樣本 

 正確分類的條件,

式中  表示樣本的類別標記。

這是一個拉格朗日優化問題，可以通過拉格朗日乘數法得到最優超平面的權重向量  和偏置  。

原始碼

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68

#include <opencv2/core/core.hpp> #include <opencv2/highgui/highgui.hpp> #include <opencv2/ml/ml.hpp> using namespace cv; int main() { // Data for visual representation int width = 512, height = 512; Mat image = Mat::zeros(height, width, CV_8UC3); // Set up training data float labels[4] = {1.0, -1.0, -1.0, -1.0}; Mat labelsMat(3, 1, CV_32FC1, labels); float trainingData[4][2] = { {501, 10}, {255, 10}, {501, 255}, {10, 501} }; Mat trainingDataMat(3, 2, CV_32FC1, trainingData); // Set up SVM's parameters CvSVMParams params; params.svm_type = CvSVM::C_SVC; params.kernel_type = CvSVM::LINEAR; params.term_crit = cvTermCriteria(CV_TERMCRIT_ITER, 100, 1e-6); // Train the SVM CvSVM SVM; SVM.train(trainingDataMat, labelsMat, Mat(), Mat(), params); Vec3b green(0,255,0), blue (255,0,0); // Show the decision regions given by the SVM for (int i = 0; i < image.rows; ++i) for (int j = 0; j < image.cols; ++j) { Mat sampleMat = (Mat_<float>(1,2) << i,j); float response = SVM.predict(sampleMat); if (response == 1) image.at<Vec3b>(j, i) = green; else if (response == -1) image.at<Vec3b>(j, i) = blue; } // Show the training data int thickness = -1; int lineType = 8; circle( image, Point(501, 10), 5, Scalar( 0, 0, 0), thickness, lineType); circle( image, Point(255, 10), 5, Scalar(255, 255, 255), thickness, lineType); circle( image, Point(501, 255), 5, Scalar(255, 255, 255), thickness, lineType); circle( image, Point( 10, 501), 5, Scalar(255, 255, 255), thickness, lineType); // Show support vectors thickness = 2; lineType = 8; int c = SVM.get_support_vector_count(); for (int i = 0; i < c; ++i) { const float* v = SVM.get_support_vector(i); circle( image, Point( (int) v[0], (int) v[1]), 6, Scalar(128, 128, 128), thickness, lineType); } imwrite("result.png", image); // save the image imshow("SVM Simple Example", image); // show it to the user waitKey(0); }

解釋

1. 建立訓練樣本

本例中的訓練樣本由分屬於兩個類別的2維點組成， 其中一類包含一個樣本點，另一類包含三個點。

float labels[4] = {1.0, -1.0, -1.0, -1.0};
float trainingData[4][2] = {{501, 10}, {255, 10}, {501, 255}, {10, 501}};

函式 CvSVM::train 要求訓練資料儲存於float型別的 Mat 結構中， 因此我們定義了以下矩陣:

Mat trainingDataMat(3, 2, CV_32FC1, trainingData);
Mat labelsMat      (3, 1, CV_32FC1, labels);

2. 設定SVM引數

   此教程中，我們以可線性分割的分屬兩類的訓練樣本簡單講解了SVM的基本原理。 然而，SVM的實際應用情形可能複雜得多 (比如非線性分割資料問題，SVM核函式的選擇問題等等)。 總而言之，我們需要在訓練之前對SVM做一些引數設定。 這些引數儲存在類 CvSVMParams 中。

   CvSVMParams params;
   params.svm_type    = CvSVM::C_SVC;
   params.kernel_type = CvSVM::LINEAR;
   params.term_crit   = cvTermCriteria(CV_TERMCRIT_ITER, 100, 1e-6);
   

   • SVM型別. 這裡我們選擇了 CvSVM::C_SVC 型別，該型別可以用於n-類分類問題 (n  2)。 這個引數定義在 CvSVMParams.svm_type 屬性中.

     Note

      

     CvSVM::C_SVC 型別的重要特徵是它可以處理非完美分類的問題 (及訓練資料不可以完全的線性分割)。在本例中這一特徵的意義並不大，因為我們的資料是可以線性分割的，我們這裡選擇它是因為它是最常被使用的SVM型別。

   • SVM 核型別. 我們沒有討論核函式，因為對於本例的樣本，核函式的討論沒有必要。然而，有必要簡單說一下核函式背後的主要思想， 核函式的目的是為了將訓練樣本對映到更有利於可線性分割的樣本集。 對映的結果是增加了樣本向量的維度，這一過程通過核函式完成。 此處我們選擇的核函式型別是 CvSVM::LINEAR 表示不需要進行對映。 該引數由 CvSVMParams.kernel_type 屬性定義。

   • 演算法終止條件. SVM訓練的過程就是一個通過 迭代 方式解決約束條件下的二次優化問題，這裡我們指定一個最大迭代次數和容許誤差，以允許演算法在適當的條件下停止計算。 該引數定義在 cvTermCriteria 結構中。

3. 訓練支援向量機

   CvSVM SVM;
   SVM.train(trainingDataMat, labelsMat, Mat(), Mat(), params);
   

4. SVM區域分割

函式 CvSVM::predict 通過重建訓練完畢的支援向量機來將輸入的樣本分類。 本例中我們通過該函式給向量空間著色， 及將影象中的每個畫素當作卡迪爾平面上的一點，每一點的著色取決於SVM對該點的分類類別：綠色表示標記為1的點，藍色表示標記為-1的點。

Vec3b green(0,255,0), blue (255,0,0);

for (int i = 0; i < image.rows; ++i)
    for (int j = 0; j < image.cols; ++j)
    {
    Mat sampleMat = (Mat_<float>(1,2) << i,j);
    float response = SVM.predict(sampleMat);

    if (response == 1)
       image.at<Vec3b>(j, i)  = green;
    else
    if (response == -1)
       image.at<Vec3b>(j, i)  = blue;
    }

5. 支援向量

   這裡用了幾個函式來獲取支援向量的資訊。 函式 CvSVM::get_support_vector_count 輸出支援向量的數量，函式 CvSVM::get_support_vector 根據輸入支援向量的索引來獲取指定位置的支援向量。 通過這一方法我們找到訓練樣本的支援向量並突出顯示它們。

   int c     = SVM.get_support_vector_count();
   
   for (int i = 0; i < c; ++i)
   {
   const float* v = SVM.get_support_vector(i); // get and then highlight with grayscale
   circle(   image,  Point( (int) v[0], (int) v[1]),   6,  Scalar(128, 128, 128), thickness, lineType);
   }
   

結果

• 程式建立了一張影象，在其中顯示了訓練樣本，其中一個類顯示為白色圓圈，另一個類顯示為黑色圓圈。
• 訓練得到SVM，並將影象的每一個畫素分類。 分類的結果將影象分為藍綠兩部分，中間線就是最優分割超平面。
• 最後支援向量通過灰色邊框加重顯示。

點到平面的距離點到線的距離平行線之間的距離超平面二、原理與推導轉自：http://blog.csdn.net/v_july_v/article/details/7624837

前言

    動筆寫這個支援向量機(support vector machine)是費了不少勁和困難的，原因很簡單，一者這個東西本身就並不好懂，要深入學習和研究下去需花費不少時間和精力，二者這個東西也不好講清楚，儘管網上已經有朋友寫得不錯了(見文末參考連結)，但在描述數學公式的時候還是顯得不夠。得益於同學白石的數學證明，我還是想嘗試寫一下，希望本文在兼顧通俗易懂的基礎上，真真正正能足以成為一篇完整概括和介紹支援向量機的導論性的文章。

    本文在寫的過程中，參考了不少資料，包括《支援向量機導論》、《統計學習方法》及網友pluskid的支援向量機系列等等，於此，還是一篇學習筆記，只是加入了自己的理解和總結，有任何不妥之處，還望海涵。全文巨集觀上整體認識支援向量機的概念和用處，微觀上深究部分定理的來龍去脈，證明及原理細節，力保邏輯清晰 & 通俗易懂。

    同時，閱讀本文時建議大家儘量使用chrome等瀏覽器，如此公式才能更好的顯示，再者，閱讀時可拿張紙和筆出來，把本文所有定理.公式都親自推導一遍或者直接列印下來（可直接列印網頁版或本文文末附的PDF，享受隨時隨地思考、演算的極致快感），在文稿上演算。

    Ok，還是那句原話，有任何問題，歡迎任何人隨時不吝指正 & 賜教，感謝。

第一層、瞭解SVM

支援向量機，因其英文名為support vector machine，故一般簡稱SVM，通俗來講，它是一種二類分類模型，其基本模型定義為特徵空間上的間隔最大的線性分類器，其學習策略便是間隔最大化，最終可轉化為一個凸二次規劃問題的求解。

1.1、分類標準的起源：Logistic迴歸

  理解SVM，咱們必須先弄清楚一個概念：線性分類器。

    給定一些資料點，它們分別屬於兩個不同的類，現在要找到一個線性分類器把這些資料分成兩類。如果用x表示資料點，用y表示類別（y可以取1或者-1，分別代表兩個不同的類），一個線性分類器的學習目標便是要在n維的資料空間中找到一個超平面（hyper plane），這個超平面的方程可以表示為（ wT中的T代表轉置）：

可能有讀者對類別取1或-1有疑問，事實上，這個1或-1的分類標準起源於logistic迴歸。

    Logistic迴歸目的是從特徵學習出一個0/1分類模型，而這個模型是將特性的線

性組合作為自變數，由於自變數的取值範圍是負無窮到正無窮。因此，使用

logistic函式（或稱作sigmoid函式）將自變數對映到(0,1)上，對映後的值被認為

是屬於y=1的概率。

  假設函式

  其中x是n維特徵向量，函式g就是logistic函式。
    而的影象是

可以看到，將無窮對映到了(0,1)。    而假設函式就是特徵屬於y=1的概率。

  從而，當我們要判別一個新來的特徵屬於哪個類時，只需求即可，若大於0.5就是y=1的類，反之屬於y=0類。

    此外，只和有關，>0，那麼，而g(z)只是用來對映，真實的類別決定權還是在於。再者，當時，=1，反之=0。如果我們只從出發，希望模型達到的目標就是讓訓練資料中y=1的特徵，而是y=0的特徵。Logistic迴歸就是要學習得到，使得正例的特徵遠大於0，負