編者注：本文作者系出門問問 NLP 工程師李理，他在這篇文章詳細敘述了AlphaGo 人工智慧背後的細節。

前言：人生如棋

回顧一下我的人生，似乎和棋是有一些關聯的。編者注：本文作者出門問問

1997 年中考後的暑假在姑父公司的機房第一次接觸電腦，當時應該是 80386 的微機。學習電腦就是學習 DOS 命令和打字，完全不懂幹什麼用的，打字尤其是五筆字型，更是學得頭疼——王旁青頭戔五一，土士二幹十寸雨……唯一的樂趣就是趁姑父不在的時候鍵入 CCH，和電腦下一盤象棋（本文象棋特指中國象棋，如果是國際象棋不會簡稱象棋）。這個軟體的棋力挺強的，至少對於我這樣業餘水平來說是這樣的。總共下來估計有一二十盤，我贏的次數也只有一兩盤，其餘的都是輸了。我第一步一般走中炮，電腦第一步總是走馬，而當第二步我上馬的時候，電腦不是走常見的屏風馬，而是起橫車，另外一側的馬都不動。從棋理的角度說，這種佈局是有問題的，中路很空虛。但是我卻找不到什麼破綻，原因可能是中局計算能力相差太遠。

當時就覺得挺神奇的，電腦竟然會下棋，而且還這麼厲害，心想我以後能不能做一個比它還厲害的軟體。

同年，IBM 的深藍擊敗了國際象棋世界冠軍卡斯帕羅夫，不過我知道這個訊息應該是在讀大學之後了。

2000 年，由於高三最後半年沉迷於電腦遊戲，高考考得不好，而且還想離家遠一點去闖蕩，就去了北京科技大學。陰差陽錯地選擇了電子資訊工程專業。這個專業在我之前只有兩屆學生，課程設計挺混亂的，有一部分電子系的課程，如數電模電等，也有部分通訊的課程，如訊號與系統。但是我對這些課程都不感興趣，自學了很多計算機的課程。

大概是在 2003 年的時候在書店看到了王小春寫的《PC 遊戲程式設計–人機博弈》，如獲至寶，學著寫過一個黑白棋的軟體。也改過光盤裡附帶原始碼的象棋程式，不過發現要寫一個超過自己水平的象棋並不容易。

2006 年考研，填報的是計算機系的人工智慧實驗室，不過分數不夠高，後來調劑到了智慧系的聽覺實驗室，做自然語言處理方向。

同年，MCTS 第一次被提出並在圍棋上卻得極大的突破；而 Hinton 通過 DBN 讓深度神經網路重新進入人們的視野。不過當時 NLP 還不流行 Deep Learning ，當時更多的還是 structured SVM、CRFs 和 Graphical Model。當時還列印過《Learning CRFs with Hierarchical Features: An Application to Go》這篇論文。

2016年，Google DeepMind 的文章被 Nature 發表，AlphaGo 擊敗歐洲冠軍樊麾並且將要在3月份挑戰李世石。

圍棋和深度學習再次大規模高熱度地出現在世人眼前。

象棋與圍棋的比較 俗與雅

如果你在公園或家門口看到一群人圍成一團，圍觀的比下棋的還多，並且出謀劃策指手畫腳，那一定是象棋。同樣在路邊攤上擺“祖傳”殘局的也一定是象棋。圍棋則“高雅”的多，所以琴棋書畫裡的棋必然是圍棋。象棋下得好，也只能在民間擺擺路邊攤。而圍棋專門有個官職叫“棋待詔”，陪皇帝下棋的。當然伴君如伴虎，陪皇帝下棋可沒有與路邊的大爺下棋輕鬆，贏了皇帝肯定不行，但老是輸或者輸得太假了也不行。要像賈玄那樣讓皇帝每次都覺得自己棋差一著，可不是簡單的事情。喜歡下圍棋的皇帝很多，比如傳說中“一子定乾坤”的李世民，《西遊記》裡魏徵夢斬涇河龍王時也是在和李世民下棋。即使圍棋下不到國手的水平能陪皇帝下棋，還是有很多達官貴人也附庸風雅的。比如《紅樓夢》裡的賈政老爺，那麼無趣的人，也是要下下圍棋的，因此很多詹光這樣的門客。賈府四位大小姐的丫鬟是琴棋書畫，迎春的丫鬟是司棋，按說迎春下棋應該很厲害，不過在書中並沒有寫迎春下棋，倒是寫惜春和妙玉下棋，惜春在角上被倒脫靴。另外探春和寶琴下棋，“探春因一塊棋受了敵，算來算去，總得了兩個眼，便折了官著兒，兩眼只瞅著棋盤，一隻手伸在盒內，只管抓棋子作想”，因此林之孝家的來請示也未聽到。

孰難孰易

圍棋似乎更“平等”一些，每個棋子除了顏色沒有什麼不同，它的重要性取決於它的位置以及整個棋盤其它棋子（包括自己和對手）的整體分佈。而象棋似乎不同，車一般都要比馬有價值，將帥的價值無窮大，雖然它沒有什麼大作用。偶爾在某些特殊情況下，虎落平陽被犬欺，車的價值可能比不上一個馬，但大部分情況下車都超過兩個馬的價值，真是“王侯將相確有種乎”！

從理想主義的角度，我更喜歡圍棋，每個棋子都是同樣的可塑性，它的重要性取決於它的位置。但是每個棋子的位置又是它自己能決定的嗎？也許在開始一盤對局之前它的位置就大致確定了！放在棋罐裡最上面的棋子當然最可能被選擇，另外位置好壞更由下棋的棋手決定，棋子本身沒有什麼決定權。

而且從現實的角度來說個體的差異確實是存在的，打籃球的話姚明就生來比其他人有優勢。

從入門的角度說，象棋的估值函式相對簡單，因此入門應該更容易一些。

MiniMax 搜尋/Alpha-Beta 剪枝和象棋

這個演算法最早是馮諾依曼提出來的。其實每一個下棋的人可能都在不自覺的使用這個演算法，只不過沒有形式化的語言描述出來而已。

第一次下棋的時候，我們很可能嘗試當前局面下所有的可能走法，然後選擇最“好”的一個局面。拿象棋來說，“好”可以比較簡單的用雙方棋子的分值來表示，一個車的價值大致相當於兩個炮，馬和炮差不多，相當於兩個士或者相，兵的價值最低。那麼很可能我們第一次走棋時就是看哪步走法能“吃”到對方的棋子，然後就走這一步。可惜下棋是兩個人的博弈，你用車吃對方一個兵，對方可能用馬把你的車吃了，這樣算下來，用一個車換一個兵，明顯是虧了。通過這樣的例子，你學到對手是在和你“作對”，你有很多走法，如果你只考慮一步，選擇最好的局面，那麼對手會在這個局面走對他有利的局面，有可能這個局面對你非常不利。所以你覺得應該要考慮兩步也就是一個回合，首先你嘗試所有的可能（當然也可能做一些裁剪，濾掉明顯不好的走法，比如沒事走動自己的老將），比如用車吃對手的卒，然後站在對手的角度選擇對手最好的走法（用馬吃你的車），然後評估一下這個局面，發現局勢對你並不有利。接著再嘗試用兵吃對手的馬，接著對手選擇用車吃你的兵，這個結果明顯對你有利。

當然隨著你計算能力的增強，你可能把搜尋的深度從 2 擴充套件到 4 或者更多。

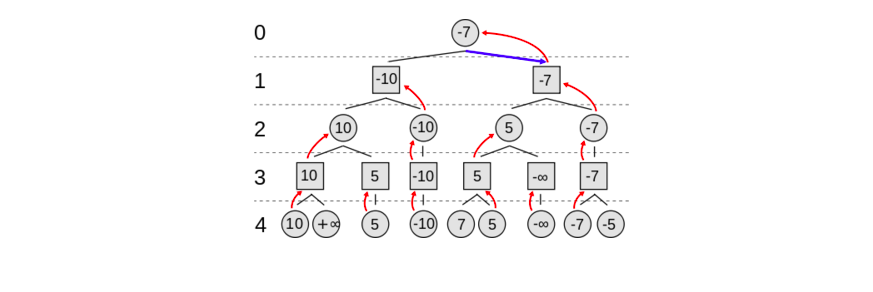
上面的“演算法”用上圖來說明。圓形的節點表示“你”面對的局面，而方塊的節點表示對手面對的局面。這裡是 4 層兩個回合的搜尋樹。

我們從最下層第 4 層開始，這一層是葉子節點，不再展開，你需要評估局面的“好壞”，比如前面描述的“簡單”算棋子分數的演算法（其實也不那麼簡單，想想第一次下棋的人怎麼知道？這是幾千年來前人總結出來的經驗！）計算出得分。

接著第 3 層對手從這些局面中選擇他最好的局面（也就是你最壞的局面），也就是得分最少的局面（因為計算得分是從你的角度計算的）。

接著你在第 2 層選擇得分最多的局面。

接著對手在第 1 層選擇得分最少的局面。

最後你在第 0 層選擇得分最多的局面。

這裡忽略或者說假設了一個非常重要的東西——估值函式。也就是之前說的怎麼評估一個局面的好壞。

對於一個遊戲來說，局面可以分為兩類：結束局面和非結束局面。比如對於象棋來說，結束局面就是一方的將/帥被吃了（實際的規則是一方的將/帥沒有“合法”的走法了。但是我們總是可以假設將帥是可以走不能走的位置，然後被“吃”掉，或者將帥碰面也可以看成被吃，我小時候學下象棋的時候就是這麼認為的），其它的所有合法局面都是非結束局面（現代象棋還有一些規則為了避免重複局面或者“無賴”的長將長打長捉指定了一些規則約束，高手過招時甚至會“合理”地利用這樣的規則，另外在某些特殊的殘棋裡這些規則也會決定勝負）。

對於很多遊戲來說，結束局面的好壞一般是遊戲規則規定的。比如象棋的結束一般是某方的將帥被吃了，那麼被吃的一方就輸了，可以認為這個局面的得分是負無窮大，而相對的另一方得分是無窮大。當然實際比賽中也有和棋，也就是雙方都沒有辦法吃掉對方的將帥或者超過自然限著的回合數。

從理論上來說，如果我們的計算能力足夠，我們可以搜尋到遊戲的結束局面，那麼我們就可以說完全“解決”了這個遊戲。但是從上面的搜尋過程我們可以發現，搜尋的節點數是隨著層次的增加指數級增加的（後面我們討論的 alph-beta 剪枝能減少部分不必要的搜尋，但是並不影響總的複雜度）。一般認為中國象棋的分支因子在 40-50 之間（也就是平均每步有這麼多種合法的走法），那麼搜尋 20 步就需要 40 的 20 次方需要多久呢？我們假設計算機每秒可以搜尋 1G 個節點（1GHz，時間一個 CPU 時鐘週期肯定不能搜尋一個節點），那麼也需要 3486528500050735 年！

因此，我們只能搜尋有限的深度，這就帶來一個問題，非結束局面的得分的計算問題。也就是給定一個局面，怎麼計算“好壞”？

首先，我們需要定義這個“好壞”。定義其實非常簡單，這個得分就是把這個局面搜尋到結束局面的得分，基本上三種可能：勝/負/和。當然這個理論得分是不知道的，那麼我們怎麼近似它呢？一種最簡單而且實際上我們人類一直在使用的方法就是統計的方法：我們看以往對弈的結果，如果這個局面下了 100 局，我方勝了 60 局，輸了 40 局，那麼我可能認為這個局面還不錯，反之如果我方勝了 30 局輸了 70 局，那麼就不太好。

當然，我們統計的是“高手”的對局，如果是隨機的對局，可能沒有統計意義。這裡其實有個雞生蛋蛋生雞的過程。類似於 EM 演算法。我們首先有一個還“不錯”的估值函式（人類高手），然後不停的模擬對局（下棋），然後統計新的局面得分，然後用這些局面得分更新我們的估值函式。

這樣一代一代的積累下來，人類的下棋水平越來越高。這其實和下面我們要討論的強化學習和 MCTS 有類似的思想！我們下面會再討論這個問題。

比如我們有了一個基本的估值函式：計算棋子的靜態得分，將 10000 分，車 10 分，馬和炮 5 分，相士 2 分，兵卒 1 分。然後我們不斷下棋，發現有些局面從棋子看雙方都一樣，但是棋子的不同位置會導致最終勝負的差距很大。因此我們會更新我們的估值函式：比如兵卒過河要變成兩分。棋子的行動力越大分越高，越靠近中間分越高，不同的棋子如果有保護或者攻擊關係，我們會增加一些分數，另外一些特殊的局面，比如空頭炮，三子歸邊會有很高的勝率，我們也會增加分數，從而出現棋子攻殺。

因此一個棋手的棋力除了計算能力（這個更多是天賦，當然也能通過訓練提高），另外一個很重要的能力就是評估局面的能力，這個就更多的靠後天的訓練。而一個遊戲是否“有趣”/“好玩”，其實也跟評估函式有關。如果一個遊戲很容易評估，那麼基本不需要搜尋，看一個回合就知道最終的結果了，就沒有什麼意思。最有“意思”的局面是“看”起來很差但“其實”很好的棋，或者看起來某個局面很平穩，但其實某方優勢很明顯，所謂的“妙手”是也。什麼叫“看”起來很差？就是搜尋很淺的層次評估或者不搜尋直接評估得分很差（比如走窩心馬或者被架空頭炮），但是搜尋很深之後發現這是當前局面下最好的走法，甚至是反敗為勝的唯一招法。高手和低手的差別也在於此，對於那種很明顯的好壞，大家都能看得出來；而有些局面，對於低手來說可能覺得局面雙方還差不多，但是在高手看來勝負早已瞭然於胸了。

Alpha-Beta 剪枝

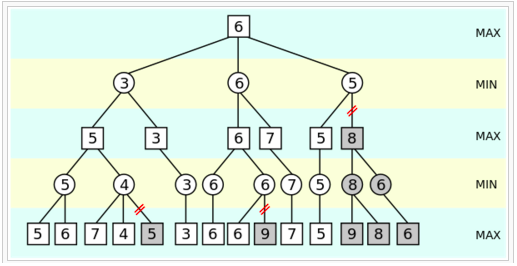
(from https://en.wikipedia.org/wiki/Alpha%E2%80%93beta_pruning)

假設 minimax 是 4 層的深度優先搜尋，並且是如圖的從左到右的順序。那麼有些子樹是不用搜索，可以被剪枝掉的。

比如下面這棵子樹：

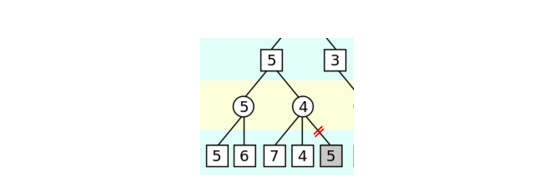
第 0 層是 MAX 操作，第一個孩子返回了 5，現在我們正準備搜尋第二個孩子（4 的那個，當然現在還不知道）。我們知道它的只至少是 5 了，>=5。

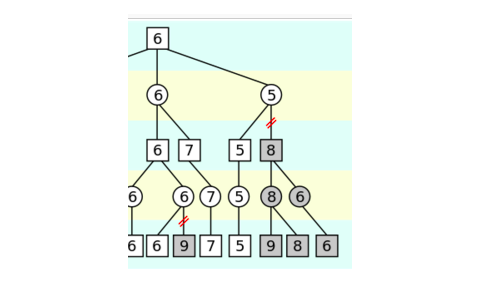
它是一個 MIN 操作，首先搜尋到 7，所以它的取值 <=7，接著搜尋到 4，所以它的取值 <=4，這個時候就可以停止了，為什麼？ 因為第 0 層的節點的值已經 >=5了，而第 1 層的右邊那個節點已經 <=4了，所以不管它的第三個孩子得分多少，第 0 層都不會選擇了，所以可以把它剪枝掉了。max（5, （<=4）)=5。 搜尋完兩個孩子之後，第 0 層的值已經 >=6了，然後搜尋第 1 層（5）的那個節點，它的第一個孩子已經返回 5 了，所以它的值必然<=5了，所以它的第二個孩子（8）也沒有必要搜尋了。因為 max（6, （<=5）)=6。 類似的，對手在 MIN 的時候也可以剪枝，min（3, （>=4）)=3。

當然上面是非常形式化的描述，其實在實際的下棋過程中我們可能自覺不自覺的使用了 alpha-beta 剪枝。

比如，我們有這樣的推理：我可以走車吃對手一個兵而且對手吃不了我任何子(得分+1)；也可以走馬吃對手的卒，走馬後對手有很多走法，其中一個走法是吃掉我的馬而且我還吃不了他任何棋子（得分-4），那麼這個時候我就不會走馬了，因為不管其餘的走法怎麼樣（也許對手還有更好的走法，比如吃我一個車得 10 分；當然也有更差的走法不吃我的子讓我得+1 分，但他不會這麼走），這個走法下我“至少”損失一個馬了，那麼我現在有一個得分+1 的走法，我就不要考慮對手其它的走法了，直接剪枝掉了。用形式化的語言描述 max（1, （<=-5））=1。

alpha-beta 能否剪枝非常依賴於搜尋的順序，如果把最優的走法先搜尋，那麼能得到最大程度的剪枝。所以這個樹的展開順序非常重要。一般會使用很多啟發式規則來排序。比如吃對方的棋子很可能是比較好的走法，而沒事走動老將不是什麼好的走法。

要下好象棋，計算能力和評估局面的能力缺一不可。因為人的計算能力有限（計算機也是一樣），所以搜尋到一定層次之後需要停下來評估局面。當然人的搜尋不是固定的，而是和評估函式一起工作的，對於“簡單”的局面（比如明顯很差或者很好的），就不要搜尋很深，而對於“複雜”的局面，則會盡可能深的搜尋下去。所以好的評估局面的能力對於下象棋很重要，這個容易理解。

那麼計算能力（搜尋深度）的重要性呢？這個似乎更加顯而易見，棋經雲：“多算勝，少算不勝，況乎無算。”

不過仔細思考一下，有似乎沒有那麼明顯。為什麼搜尋深比搜尋淺好呢？除非你能搜尋到遊戲結束，否則都得提前結束使用估值函式。搜尋深比搜尋淺好的一個隱含假設就是越深的局面越容易評估。對於象棋來說這是很明顯的，因為象棋的特定是越下棋子越少，局面也就更容易評估。而圍棋就不一樣，棋子越到後來越多，局面的評估難度並沒有明顯的下降（甚至可能上升，我個人圍棋水平也就是會簡單規則的程度，所以很可能不是這樣）。當然圍棋的評估局面比象棋也複雜很多（至少我是這麼覺得的）。

當然一個人的計算能力是有限的，所以“離線”的計算對於職業棋手也很重要。很多棋手對於某些佈局有非常細緻的研究，他們“離線”研究了各種可能的變化，因此你如果走到了他熟悉的佈局，你基本上很難戰勝他。因此殘局庫和開局庫的研究和記憶是一個職業棋手努力的方向。

要設計一個好的象棋程式也是一樣，首先是計算（搜尋）能力，這個對於相對於人類來說是它的強項。因此更關鍵的就是評估局面的函式。由於象棋的局面特徵還是比較明顯的，靜態的棋子分值估計能解決 80%的局面，再加上一下位置特徵（比如棋子在不同的位置有不同的加減分），棋子的行動力，棋子之間的保護關係等等，就能解決大部分的局面。那些非常複雜的局面可以通過更深的搜尋層次來解決。另外像開局庫，殘局庫這些對於計算機都不是問題，它的記憶能力遠超人類。

有了這些重要的特徵，可以人工設計估值函式，也可以用機器學習的方法學習更加準確的估值函式。所以解決象棋應該是“比較”容易的（相對於圍棋）。所以現在國際象棋人類的水平和計算機差距越來越大，人類幾乎沒有獲勝的可能了。

圍棋為什麼不能用類似的方法

國際象棋解決之後，大家把注意力放到了圍棋上。用類似的方法效果很差，比如 GnuGo 的棋力大概在 13 級(kyu)。

13 級什麼概念呢？從下圖中可以看到是非常差的水平。

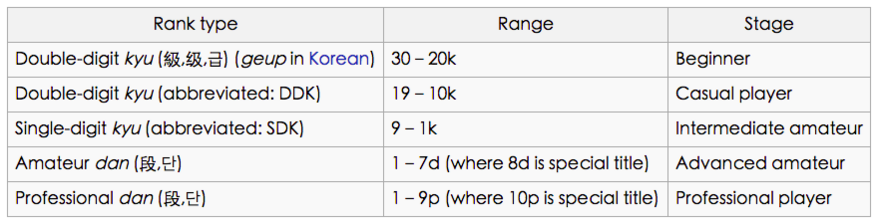
(from https://en.wikipedia.org/wiki/Go_ranks_and_ratings#Kyu_and_dan_ranks)

為什麼對於象棋非常有效的方法用在圍棋上就不行呢？我們需要分析兩種棋的差別。不過由於我本人下棋水平一般，圍棋更是剛入門的水平，所以更多的是從程式設計師的角度來分析兩種棋的差異。

分支因子和深度

國際象棋的分支因子是 35，而圍棋是 250（https://en.wikipedia.org/wiki/Branching_factor）。這個數值只是估計，但可以看出大致的差別。從這個角度來說圍棋要比國際象棋複雜。但如果只是這一個因素的差別不可能導致最好的國際象棋程式超過人類而圍棋只有 13k 的水平。

估值函式

前面我們分析的是中國象棋，國際象棋和中國象棋類似，所以它的估值函式是相對容易和準確的。而圍棋就比較困難，數棋子的個數明顯是沒有任何用處的。

“圍棋難的地方在於它的估值函式非常不平滑，差一個子盤面就可能天翻地覆，同時狀態空間大，也沒有全域性的結構。這兩點加起來，迫使目前計算機只能用窮舉法並且因此進展緩慢。但人能下得好，能在幾百個選擇中知道哪幾個位置值得考慮，說明它的估值函式是有規律的。這些規律遠遠不是幾條簡單公式所能概括，但所需的資訊量還是要比狀態空間本身的數目要少得多（得多）。”

（http://www.almosthuman.cn/2016/01/12/ebfzg/）

後面我討論用深度學習(CNN)來評估局面時會分析這兩個因素哪個更重要，至少從個人感覺來看，第二個更加重要一些。

圍棋和象棋的差別還是挺大的，比如 MCTS 搜尋，在圍棋中效果不錯，但是用到象棋裡就沒有什麼效果。

MCTS 多臂老虎機(Multi-Arm Bandits) 和 UCB(Upper Confidence Bounds)

這是強化學習裡最簡單的一個問題，在很多地方都有應用，比如網際網路廣告(https://support.google.com/analytics/answer/2844870?hl=en)，遊戲廳有一個 K 臂的老虎機，你可以選擇其中的一個投幣，每個手臂都是一個產生一個隨機的獎勵，它們的均值是固定的（也有 Nonstationary 的多臂老虎機，我這裡只考慮 Stationary 的）。你有 N 次投幣的機會，需要想辦法獲得最大的回報(reward)。

當然如果我們知道這個 K 個手臂的均值，那麼我們每次都選擇均值最大的那個投幣，那麼獲得的期望回報應該是最大的。

可惜我們並不知道。那麼我們可能上來每個都試一下，然後接下來一直選擇最大的那個。不過這樣可能也有問題，因為獎勵是隨機的，所以一次回報高不代表真實的均值回報高。當然你可以每個都試兩次，估計一下獎勵的均值。如果還不放心，你可以每個都試三次，或者更多。根據大數定律，試的次數越多，估計的就越準。最極端的一種做法就是每個手臂都投一樣多的次數；另外一種極端就是碰運氣，把所有的機會都放到一個手臂上。後一種如果運氣好是最優的，但是很可能你抽到的是回報一般的甚至很差的手臂，期望的回報其實就是 K 個手臂的平均值。前一種呢？回報也是 K 個手臂的平均值！我們實際的做法可能是先每個手臂都試探幾次，然後估計出比較好的手臂（甚至幾個手臂），然後後面重點嘗試這個（些）手臂，當然偶爾也要試試不那麼好的手臂，太差的可能就不怎麼去試了。但這個“度”怎麼控制就是一個很複雜的問題了。這就是 exploit-explore 的困境(dilemma)。利用之前的經驗，優先“好”的手臂，這就是 exploit；嘗試目前看不那麼“好”的手臂，挖掘“潛力股”，這就是 explore。

一種策略(Policy)的 Regret （損失）為：

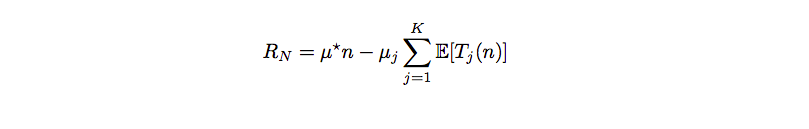
(from A Survey of Monte Carlo tree Search Methods)

我覺得 mu_j 應該放到求和符號裡面的。

不要被數學公式嚇到了，用自然語言描述就是：最理想的情況是 n 次都試均值最大的那個手臂(mu star)，不過我們並不知道，E[Tj(n)] 是這個策略下選擇第 j 個手臂的期望。那麼 R 就是期望的損失，如果我們的策略非常理想，這個策略只嘗試最好的手臂，其它不試，那麼 R 就是 0。

但是這樣的理想情況存在嗎？很明顯不太可能存在（存在的一種情況是k個手臂的均值一樣）。那麼我們的策略應該儘量減少這個損失。

Lai and Robbins 證明了這個損失的下界是 logn，也就是說不存在更好的策略，它的損失比 logn 小（這類似於演算法的大 O 表示法）。

所以我們的目標是尋找一種演算法，它的損失是 logn 的。

UCB 就是其中的一種演算法：

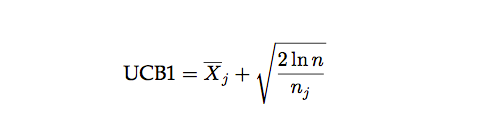
每次決策之前，它都用上面的公式計算每個手臂的 UCB 值，然後選中最大的那個手臂。公式右邊的第一項是 exploit 項，是第 j 個手臂的平均回報的估計。這個值越大我們就越有可能再次選中它。第二項是 explore 項，n_j 是第 j 個手臂的嘗試次數，n_j 越小這個值就越大，也就是說嘗試次數越少的我們就越應該多嘗試。當 n_j=0 時，第二項為無窮大，所以這個演算法會首先嚐試完所有的手臂（explore），然後才會選擇回報最大的那個(exploit)，試了之後這個手臂的平均值可能變化，而且 n_j 增加，explore 值變小，接著可能還是試最大的那個，也可能是第二大的，這要看具體情況。

我們來分析一些極端的情況，一種情況是最好的（假設下標是 k)比第二好的要好很多，那麼第一項佔主導，那麼穩定了之後大部分嘗試都是最好的這個，當然隨著 n_k 的增加 explore 項在減少(其它手錶不變)，所以偶爾也試試其它手臂，但其它手臂的回報很少，所以很快又會回到第 k 個手臂。但是不管怎麼樣，即使 n 趨於無窮大，偶爾也會嘗試一下其它的手臂的。不過因為大部分時間都在第 k 個手臂上，所以直覺上這個策略還是可以的。

另一種極端就是 k 個手臂都差不多（比如都是一樣的回報），那麼 exploit 項大家都差不多，起決定作用的就是 explore 項，那麼就是平均的嘗試這些手臂，由於 k 各手臂回報差不多，所以這個策略也還不錯。 出於中間的情況就是有一些好的和一些差的，那麼根據分析，大部分嘗試都是在好的手臂上，偶爾也會試一試差的，所以策略的結果也不會太差。

當然這個只是簡單的直覺的分析，事實上可以證明這個演算法的 regret 是 logn 的，具體證明細節請參看論文《Finite-time Analysis of the Multiarmed Bandit Problem》。

MCTS（Monte Carlo tree Search）和 UCT（Upper Confidence Bound for trees）

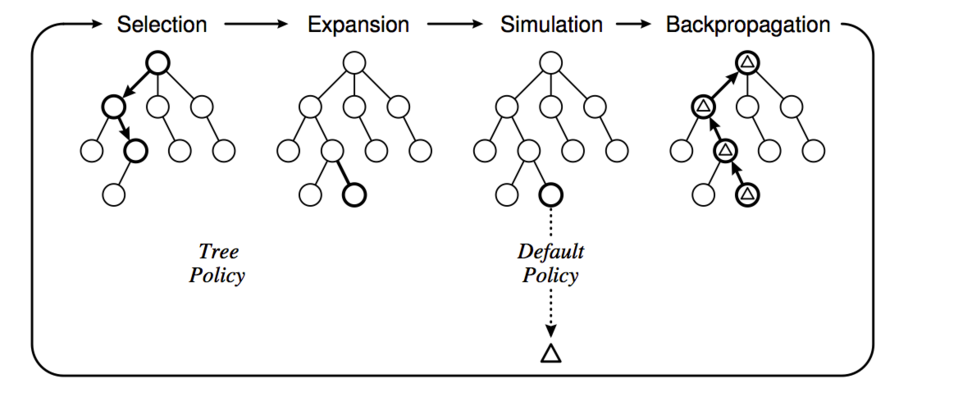
(from A Survey of Monte Carlo tree Search Methods)

MCTS 演算法就是從根節點（當前待評估局面）開始不斷構建搜尋樹的過程。具體可以分成 4 個步驟，如上圖所示。

1. Selection

使用一種 Policy 從根節點開始，選擇一個最“緊急”(urgent)的需要展開(expand)的可以展開(expandable)的節點。

說起來有點繞口，可以展開的節點是非葉子節點（非遊戲結束局面），而且至少還有一個孩子沒有搜尋過。比如上圖展示的選擇過程，最終選擇到的節點不一定是葉子節點（只有它還有沒有搜尋過的孩子就行）。具體的選擇策略我們下面會討論。

2. Expansion

選中節點的一個或者多個孩子被展開並加入搜尋樹，上圖的 Expansion 部分展示了展開一個孩子並加入搜尋樹的過程。

3. Simulation

從這個展開的孩子開始模擬對局到結束，模擬使用的策略叫 Default Policy。

4. Backpropagation

遊戲結束有個得分（勝負），這個得分從展開的孩子往上回溯到根節點，更新這些節點的統計量，這些統計量會影響下一次迭代演算法的 Selection 和 Expansion。

經過足夠多次數的迭代之後（或者時間用完），我們根據某種策略選擇根節點最好的一個孩子（比如訪問次數最多，得分最高等等）。

上面的演算法有兩個 policy：tree policy 和 default policy。tree policy 決定怎麼選擇節點以及展開；而 default policy 用於 simulation（也有文獻叫 playout，就是玩下去直到遊戲結束)

在討論 MCTS 和 UCT 之前，我們來分析一下人在下棋時的搜尋過程。

首先人的搜尋肯定不是之前的固定層次的搜尋的，很多“明顯”不“好”的局面可能就只搜尋很淺的層次，而不那麼“明顯”的局面可能需要搜尋更深的層次（之前我們討論過這裡隱含了一個假設：深的局面比淺的局面容易評估，對於象棋這是比較明顯的），“好”的局面也需要多搜尋幾層確保不會“看走眼”。

MCTS 其實有類似的思想：我們著重搜尋更 urgent 的孩子，所謂 urgent，就是更 promising 的孩子。當然偶爾也要看看那些不那麼 promising 的孩子，說不定是潛力股。這其實就有之前討論的 exploit 和 explore 的平衡的問題。

另外 MCTS 直接 Simulation 到對局的結束，“迴避”了局面評估的難題（不過這個問題最終還是繞不過去的，我們下面會再討論）。

既然是 exploit 和 explore 的問題，那麼之前我們討論的 UCB 就可以直接用上了，把 UCB 用到 MCTS 就是 UCT 演算法（注意： MCTS 其實是一族演算法的統稱，不同的 tree Policy 和 Default Policy 就是不同的 MCTS 演算法）.

UCT 演算法

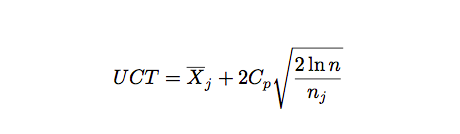
Selection 和 Expansion 的公式如上，和 UCB 很類似，只是多了一個常量 Cp，用來平衡 exploit 和 explore。

相關推薦