人口預測模型Matlab實現Logistic曲線模型
阿新 • • 發佈:2019-01-05
資料:
| 年份 | 時間變數t=年份-1970 | 人口y | 年份 | 時間變數t=年份-1970 | 人口y |
| 1971 | 1 | 33815 | 1986 | 16 | 34520 |
| 1972 | 2 | 33981 | 1987 | 17 | 34507 |
| 1973 | 3 | 34004 | 1988 | 18 | 34509 |
| 1974 | 4 | 34165 | 1989 | 19 | 34521 |
| 1975 | 5 | 34212 | 1990 | 20 | 34513 |
| 1976 | 6 | 34217 | 1991 | 21 | 34515 |
| 1977 | 7 | 34344 | 1992 | 22 | 34517 |
| 1978 | 8 | 34458 | 1993 | 23 | 34519 |
| 1979 | 9 | 34498 | 1994 | 24 | 34519 |
| 1980 | 10 | 34476 | 1995 | 25 | 34521 |
| 1981 | 11 | 34483 | 1996 | 26 | 34521 |
| 1982 | 12 | 34488 | 1997 | 27 | 34523 |
| 1983 | 13 | 34513 | 1998 | 28 | 34525 |
| 1984 | 14 | 34497 | 1999 | 29 | 34525 |
| 1985 | 15 | 34511 | 2000 | 30 | 34527 |
Logistic模型的基本形式是:
y=1/(a+b*exp(-t))
所以令y'=1/y; x'=exp(-t)強曲線轉化成直線模型
y'=a+b*x'
Matlab程式碼進行分析擬合計算:
程式碼一:(資料較少時刻意採用這種方式,直接在程式碼中輸入資料)
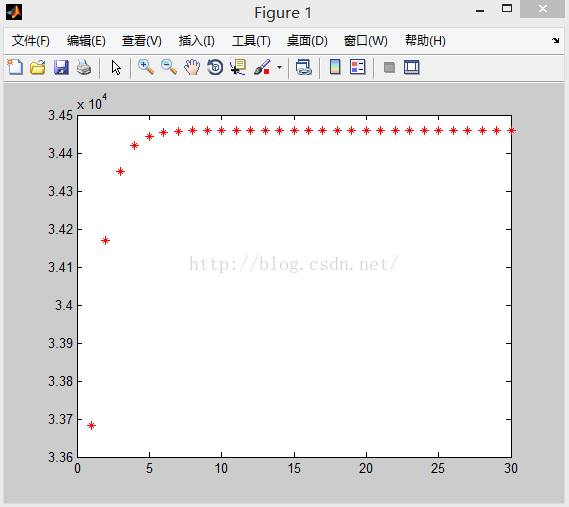
clear clc % 讀入人口資料(1971-2000年) Y=[33815 33981 34004 34165 34212 34327 34344 34458 34498 34476 34483 34488 34513 34497 34511 34520 34507 34509 34521 34513 34515 34517 34519 34519 34521 34521 34523 34525 34525 34527] % 讀入時間變數資料(t=年份-1970) T=[1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30] % 線性化處理 for t = 1:30, x(t)=exp(-t); y(t)=1/Y(t); end % 計算,並輸出迴歸係數B,即計算迴歸方程 y'=a+bx' 中的a和b的值 c=zeros(30,1)+1; X=[c,x'];%相當於30個方程組,求解a和b 的值. B=inv(X'*X)*X'*y' for i=1:30, % 計算迴歸擬合值 z(i)=B(1,1)+B(2,1)*x(i); % 計算離差 s(i)=y(i)-sum(y)/30; % 計算誤差 w(i)=z(i)-y(i); end % 計算離差平方和S S=s*s'; % 迴歸誤差平方和Q Q=w*w'; % 計算迴歸平方和U U=S-Q; % 計算,並輸出F檢驗值 F=28*U/Q % 計算非線性迴歸模型的擬合值 for j=1:30, Y(j)=1/(B(1,1)+B(2,1)*exp(-j)); end % 輸出非線性迴歸模型的擬合曲線(Logisic曲線) plot(T,Y,'r*')
擬合圖形:
改進的程式碼(當資料較多時,從Excel中讀取資料):
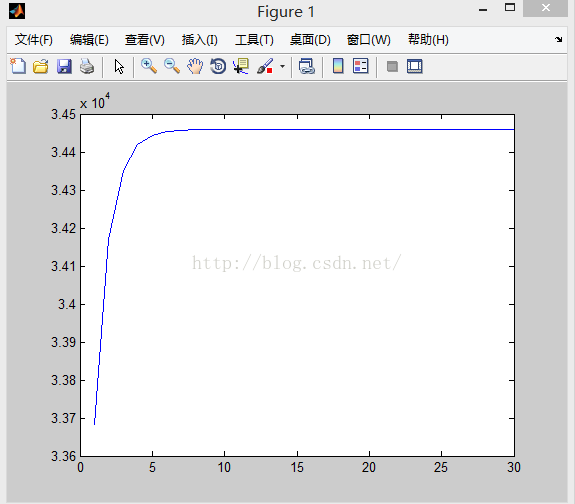
clear clc Y=xlsread('D:\sun1.xlsx',1,'B1:B30');%讀取資料 Y=Y'; T=xlsread('D:\sun1.xlsx',1,'A1:A30');%讀取資料 T=T'; for t=1:30, x(t)=exp(-t); y(t)=1/Y(t); end c=zeros(30,1)+1; X=[c,x']; B=inv(X'*X)*X'*y'%B=inv(X'*X)*X'*y' for i=1:30, z(i)=B(1,1)+B(2,1)*x(i); s(i)=y(i)-sum(y)/30; w(i)=z(i)-y(i); end S=s*s'; Q=w*w'; U=S-Q; F=28*U/Q for j=1:30, Y(j)=1/(B(1,1)+B(2,1)*exp(-j)); end plot(T,Y)
擬合曲線圖形:
輸出結果:
迴歸係數B及F檢驗值:
B =
1.0e-04 *
0.2902
0.0182
F =
47.8774