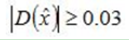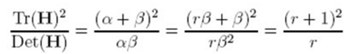SIFT演算法描述
本博文下載地址:http://pan.baidu.com/s/1geTrV5D
SIFT特徵提取演算法流程:
1、 輸入影象
2、 多尺度空間極值點檢測
3、 關鍵點的精確定位
4、 關鍵點的主方向計算
6、 特徵向量
2、多尺度空間極值點檢測
尺度空間:目的是檢測在尺度變化時仍然穩定的特徵;
影象I(x,y)的尺度空間定義:L(x,y,σ)=G(x,y,σ)*I(x,y)
尺度引數σ,當σ 連續變化,G(x,y,σ)構成影象的尺度空間。
高斯差分尺度空間:為了在尺度空間中檢測穩定的關鍵點,構造高斯差分尺度空間
D(x,y,σ)=[ G(x,y,kσ) - G(x,y,σ) ]* I(x,y) = L(x,y,kσ)- L(x,y,σ)
幾個理由:
1) 計算效率高:高斯卷積,減法
2) 高斯差分是對尺度歸一化LoG的一個很好的近似, 而尺度歸一化的LoG空間具有真正的尺度不變性。
3) 實驗比較表明,從尺度歸一化LoG空間中提取的影象特徵的尺度穩定性最好,優於梯度、Hessian或Harris角點函式。DoG運算元是尺度歸一化的LoG運算元的近似,因此計算比較簡單。
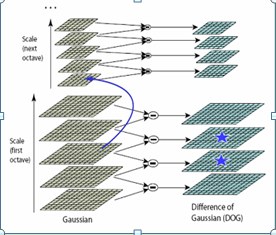
(2)將每一組尺度空間中的相鄰高斯尺度函式相減,生成高斯差分金字塔:建立成了3維尺度空間形式。
(3)極值點檢測:在三維尺度空間中,搜尋每個點的26鄰域,若該點為區域性極值點則儲存為候選關鍵點。
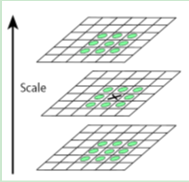
3、關鍵點的精確定位
由上一步得到的候選關鍵點,需要進行精確的定位,也就是要確定這個特徵點的位置和尺度以及主曲率。
首先,對尺度空間D(x,y,σ)進行二次泰勒展開,再利用二次泰勒展開式進行最小二乘擬合。然後通過計算擬合曲面的極值來進一步確定影象特徵點的尺度和影象特徵點的位置。
1) 去除低對比度點
將尺度空間函式進行泰勒展開:
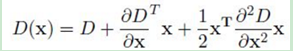
對上式求導,並令其為0,得到精確的位置, 得:
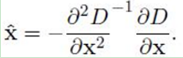
2)在已經檢測到的特徵點中,要去掉低對比度的特徵點和不穩定的邊緣響應點。並將其帶入到D(x)中,
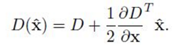
如果
則保留該特徵點,否則丟棄(低對比度候選特徵點)。
3)去除邊緣處的特徵點
由於邊緣極值點的抗噪能力差,為了得到穩定的極值點,需要去除邊緣的影響。由於每個特徵點都有兩個主方向,這兩個主方向的法曲率分別是曲面在該點法曲率的最大值和最小值。我們用這兩個值做比,比值大於設定的閾值時,該極值點被認為在邊緣上,否則為非邊緣極值點。
主曲率通過Hessian矩陣H求得:
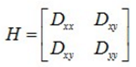
其中:
Dxx=D(x+1,y)+D(x-1,y)-2*D(x,y)
Dyy==D(x,y+1)+D(x,y-1)-2*D(x,y)
Dxy=0.25*[D(x+1,y+1)+D(x+1,y-1)-(D(x-1,y+1)-D(x-1,y-1)]
通過矩陣求解,假設α是H的最大特徵值,β是H的最小特徵值。則矩陣的跡Tr(H)和矩陣行列式的值Det(H)分別為:Tr(H)= Dxx +Dyy=α+β;Det(H)= Dxx *Dyy - Dxy2=α*β
令α=rβ;(r + 1)2/r的值在兩個特徵值相等的時候最小,隨著r的增大而增大,因此,為了檢測主曲率是否在某域值r下,只需檢測:
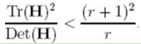
如果:(α+β)/ αβ>(r+1)2/r,則丟棄。在Lowe的文章中,取r=10。
4、關鍵點的主方向計算
上一步中確定了每幅圖中的特徵點,為每個特徵點計算一個方向,依照這個方向做進一步的計算, 利用關鍵點鄰域畫素的梯度方向分佈特性為每個關鍵點指定方向引數,使運算元具備旋轉不變性。
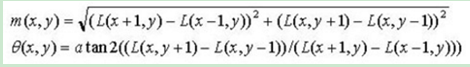
為(x,y)處梯度的模值和方向公式。其中L所用的尺度為每個關鍵點各自所在的尺度。至此,影象的關鍵點已經檢測完畢,每個關鍵點有三個資訊:位置,所處尺度、方向,由此可以確定一個SIFT特徵區域。
梯度直方圖的範圍是0~360度,其中每10度一個柱,總共36個柱。隨著距中心點越遠的領域其對直方圖的貢獻也響應減小.Lowe論文中還提到要使用高斯函式對直方圖進行平滑,減少突變的影響。
在實際計算時,我們在以關鍵點為中心的鄰域視窗內取樣,並用直方圖統計鄰域畫素的梯度方向。梯度直方圖的範圍是0~360度,其中每45度一個柱,總共8個柱, 或者每10度一個柱,總共36個柱。Lowe論文中還提到要使用高斯函式對直方圖進行平滑,減少突變的影響。直方圖的峰值則代表了該關鍵點處鄰域梯度的主方向,即作為該關鍵點的方向。(直方圖中的峰值就是主方向,其他的達到最大值80%的方向可作為輔助方向)
5、描述子的構造
特徵點在確定了位置和尺寸之後,下一步就是根據特徵點周圍的區域性特徵計算一個特徵描述子,其生成過程如下:
1) 旋轉座標。使座標軸旋轉為特徵點方向上,確保旋轉不變性。
2) 在旋轉後的影象上,以特徵點為中心取8*8大小的視窗,設特徵點位於該視窗的中央位置,特徵點周圍的方格代表特徵點的領域範圍,每個小方格代表一個畫素,在每個畫素上計算梯度。箭頭的方向和長度分別表示畫素的方向和模值。
3) 將視窗平均分為4*4的子視窗,再利用高斯模糊方法增加與特徵點鄰近域的權重值、降低特徵點較遠的權重值,最後計算每個區域的0°、45°、90°、135°、180°、225°、270°、315°方向的梯度累加值,便可以得到特徵描述子的特徵向量。這時的SIFT特徵向量已經取出來對旋轉和尺度變化帶來的影響。最後進行灰度值的歸一化,消除光線的影響。
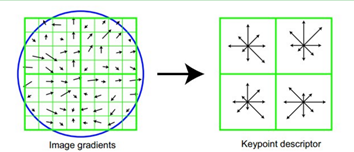
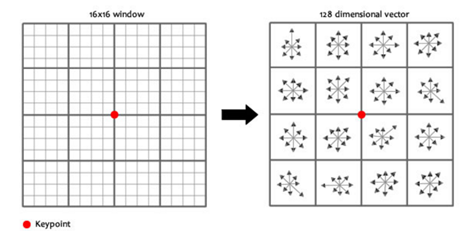
(圖左部分的中央為當前關鍵點的位置,每個小格代表關鍵點鄰域所在尺度空間的一個畫素,利用公式求得每個畫素的梯度幅值與梯度方向,箭頭方向代表該畫素的梯度方向,箭頭長度代表梯度模值,然後用高斯視窗對其進行加權運算。)
圖中藍色的圈代表高斯加權的範圍(越靠近關鍵點的畫素梯度方向資訊貢獻越大)。然後在每4×4的小塊上計算8個方向的梯度方向直方圖,繪製每個梯度方向的累加值,即可形成一個種子點,如圖右部分示。此圖中一個關鍵點由2×2共4個種子點組成,每個種子點有8個方向向量資訊。這種鄰域方向性資訊聯合的思想增強了演算法抗噪聲的能力,同時對於含有定位誤差的特徵匹配也提供了較好的容錯性。
計算keypoint周圍的16*16的window中每一個畫素的梯度,而且使用高斯下降函式降低遠離中心的權重。
在每個4*4的1/16象限中,通過加權梯度值加到直方圖8個方向區間中的一個,計算出一個梯度方向直方圖。這樣就可以對每個feature形成一個4*4*8=128維的描述子,每一維都可以表示4*4個格子中一個的scale/orientation. 將這個向量歸一化之後,就進一步去除了光照的影響。
當兩幅影象的SIFT特徵向量生成後,下一步我們採用關鍵點特徵向量的歐式距離來作為兩幅影象中關鍵點的相似性判定度量。
取影象1中的某個關鍵點,並找出其與影象2中歐式距離最近的前兩個關鍵點,在這兩個關鍵點中,如果最近的距離除以次近的距離少於某個比例閾值,則接受這一對匹配點。降低這個比例閾值,SIFT匹配點數目會減少,但更加穩定。為了排除因為影象遮擋和背景混亂而產生的無匹配關係的關鍵點,Lowe提出了比較最近鄰距離與次近鄰距離的方法,距離比率ratio小於某個閾值的認為是正確匹配。因為對於錯誤匹配,由於特徵空間的高維性,相似的距離可能有大量其他的錯誤匹配,從而它的ratio值比較高。Lowe推薦ratio的閾值為0.8。但作者對大量任意存在尺度、旋轉和亮度變化的兩幅圖片進行匹配,結果表明ratio取值在0. 4~0. 6之間最佳,小於0. 4的很少有匹配點,大於0. 6的則存在大量錯誤匹配點。(如果這個地方你要改進,最好給出一個匹配率和ration之間的關係圖,這樣才有說服力)作者建議ratio的取值原則如下:
ratio=0. 4 對於準確度要求高的匹配;
ratio=0. 6 對於匹配點數目要求比較多的匹配;
ratio=0. 5 一般情況下。
也可按如下原則:當最近鄰距離<200時ratio=0. 6,反之ratio=0. 4。ratio的取值策略能排分錯誤匹配點。
參考的資料連結:
[2] http://www.docin.com/p-961006321-f4.html