PCA降維-協方差
如果對協方差不清楚的 點選這裡《協方差的直觀理解》
協方差矩陣
對於多維度資料通過協方差矩陣描述各個維度間的變換關係,而不是各個樣本的之間的關係,對角線上是方差,非對角線是協方差;協方差為0時兩者獨立,其絕對值越大,兩者對彼此的影響越大。
\[ C=\begin{pmatrix} cov(x,x)& cov(x,y)& cov(x,z)\\ cov(y,x)& cov(y,y)& cov(y,z)\\ cov(z,x)& cov(z,y)& cov(z,z) \end{pmatrix} \]
可見,協方差矩陣是一個對稱的矩陣,而且對角線是各個維度上的方差。
理解協方差矩陣的關鍵就在於牢記它計算的是不同維度之間的協方差,而不是不同樣本之間,拿到一個樣本矩陣,我們最先要明確的就是一行是一個樣本還是一個維度,心中明確這個整個計算過程. ‘
機器學習-降維方法
降維不僅可以降低資料維度,減少計算量,便於優化,更可以可以去除資料噪點,其更深層次的意義在於有效資訊的提取綜合及無用資訊的擯棄。因為在降維的過程中,會選擇最大化分散程度的方向。便於提取具有跟大特徵意義的維度。
目的
資料降維的目的:資料降維,直觀地好處是維度降低了,便於計算和視覺化,其更深層次的意義在於有效資訊的提取綜合及無用資訊的擯棄。
好處
降維可以方便資料視覺化+資料分析+資料壓縮+資料提取等。
方法
**對映方法 _**線性對映方法:PCA、LDA、SVD分解等
PCA(Principal Component Analysis)
PCA方法簡介 主成分分析的思想,就是線性代數裡面的K-L變換,就是在均方誤差準則下失真最小的一種變換。是將原空間變換到特徵向量空間內,數學表示為Ax=λx。
通俗理解:就是找出一個最主要的特徵,然後進行分析。最大化投影后資料的方差(讓資料更分散),如果投影到線上,發現數據越緊密,那麼模型越難將這些點區分.
思想
• 投影后樣本越分散,保留的資訊越多
PCA優缺點:
優點:1)最小誤差。2)提取了主要資訊
缺點:1)計算協方差矩陣,計算量大
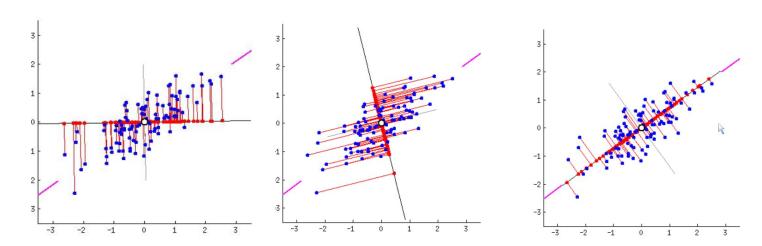
PCA步驟
假設原始資料是10(行,樣例數,y1-y10)*10(列,特徵數x1-x10)的(10個樣例,每樣例對應10個特徵)
(1)、分別求各特徵(列)的均值並對應減去所求均值。
(2)、求特徵協方差矩陣
對角線上是方差,非對角線是協方差;協方差為0時兩者獨立,其絕對值越大,兩者對彼此的影響越大。
(3)、求協方差陣的特徵值和特徵向量。
(4)、將特徵值按照從大到小排序,選擇其中最大的k個。將其對應的k個特徵向量分別作為列向量組成特徵向量矩陣。
這個矩陣就是我們要求的特徵矩陣(也稱特徵臉),裡面每一列就為樣本的一維主成分。把樣本矩陣投影到以該矩陣為基的新空間中,便可以將n維資料降低成k維資料。
(5)、將樣本點投影到選取的k個特徵向量上。
這裡需要捋一捋,若原始資料中樣例數為m,特徵數為n,減去均值後的樣本矩陣仍為MatrixDATA(m,n);
協方差矩陣是C(n,n);
特徵向量矩陣為EigenMatrix(n,k);
投影可得: FinalDATA(m,k)=MatrixDATA(m,n) * EigenMatrix(n,k) 。 