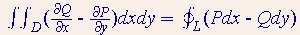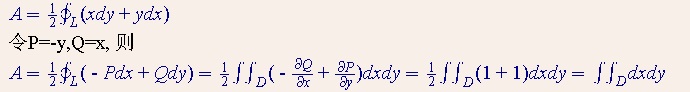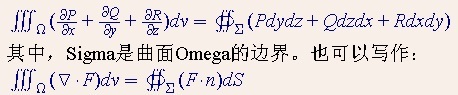首先說說格林公式（Green's theorem）。對於一段封閉曲線，若其圍城的區域D為單連通區域（內部任意曲線圍城的區域都屬於院區域），則有如下公式：

其中其中L為D的邊界，取正方向。如果沿著L前進，左邊是D的內部區域，那麼此時的L定義為正方向。

利用格林公式求面積的方法：曲線圍成的區域的面積為：

格林是十八世紀英國自學成才的數學家，他只上過一年學。1828年格林三十五歲的時候，把他當時對數學的研究寫成小冊子分發給民眾。五年後，在一位鄉野數學家的幫助下，他得以進入了劍橋大學學習。但是，格林在其短暫的一生中默默無名。

1841年，格林逝世。

1842年，一位年輕的數學家斯托克斯和物理學家開爾文發表了格林公式的推廣形式。斯托克斯是愛爾蘭人，曾就讀於劍橋大學，他當年只有23歲。所謂的斯托克斯定理(Stokes' Theorem)

可以看出，左式裡面跟向量場的旋度是一樣的，所以斯托克斯定理也叫旋度定理。

除此之外，斯托克斯發表了一系列流體力學相關的論文，並提出了著名的納維－斯托克斯方程（Navier-Stokes equations）。見下文：

納維－斯托克斯方程與傳統的理論研究方法相比，使用了通量的方法來描述物件，而不是通常的速度或加速度等物理量。

高斯散度定理(Divergence theorem)

高斯散度定理，或稱高斯定理（Gauss's theorem），也可以算是斯托克斯定理的特例。

其中，n為向量F在Sigma外側法向量上的投影。

高斯定理的直觀含義為，某個區域流出量的通量，等於所有流出點和流入點量的差。