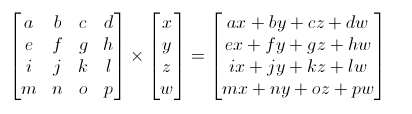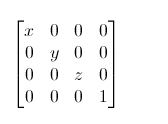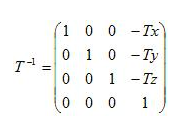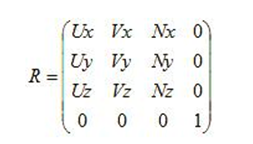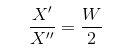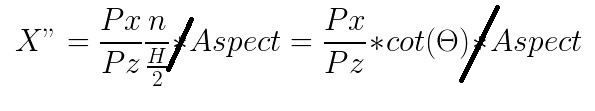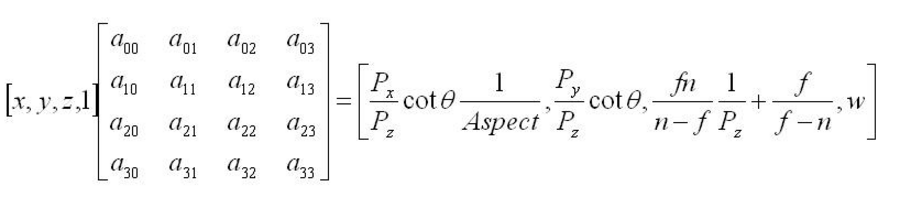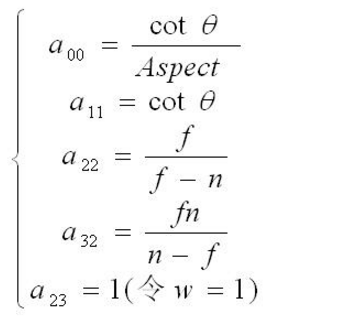說明

在這一節中，我們將一步步的從基礎構起，完成由3D物體座標轉換為到螢幕上所看到的影象的變換流程，最終反映在程式中便是我們輸入的三位點依據我們設定的觀察方式投影到了螢幕上。這部分內容可以參考《計算機圖形學》第四版。

首先明白幾個概念。

1.    模型座標系，在此座標系下構建我們的3D物體（一般以物體幾何中心為座標中心）。

2.    世界座標系，擁有所有3D物體的整個3D世界。

3.    相機座標系，該座標系是以觀察用相機（我們眼睛）為中心。

4.    裁剪空間，我理解為我們所劃定的能觀察到的相機座標系中的部分，其實還在相機座標系中

5.    標準裝置空間，我理解為我們最終投影到的位置在【-1，1】之間。

6.    螢幕空間，將【-1，1】對映到螢幕的大小下。

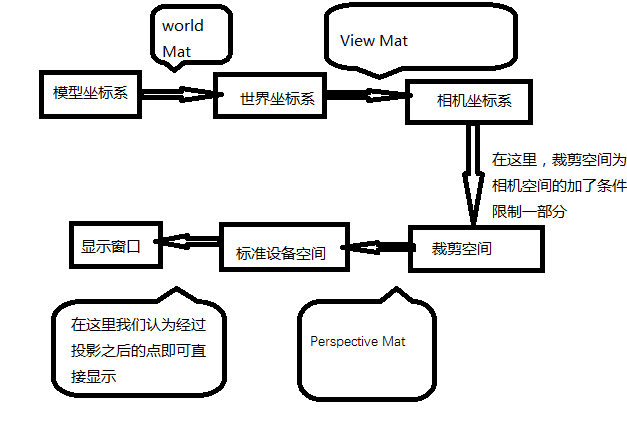
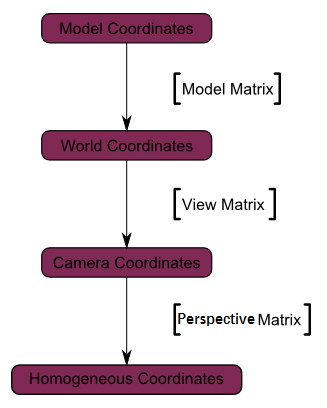
整個轉換流程是

其中裁剪空間我們在透視矩陣中即可設定，表現為一個可視截楔形臺。

具體看下面的流程

我們此時所處為相機空間，也就是說當一個點x==0,y==0時應在螢幕中心，但是由於人眼的透視效果，我們不可只用x與y來確定一個物體應放在螢幕哪部分，所以使用到相機的距離Z，當一點x,y座標相等，我們依據Z來判斷哪一個更應放在螢幕中。

 

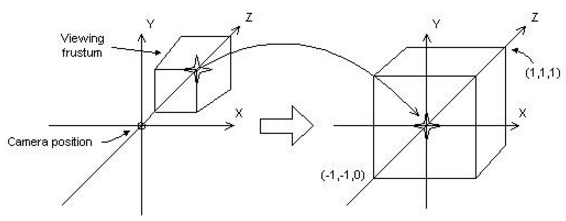
藉助圖形，在投影前，藍色為世界座標系中物體，紅色部分為相機視角下能看見的地方。

對物體使用透視矩陣後

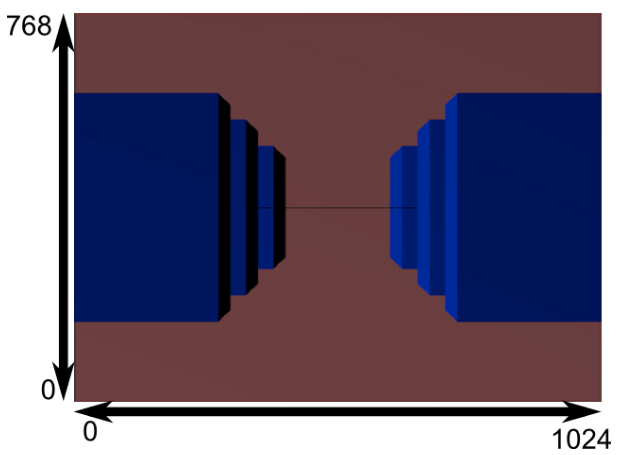
每一個錐臺都是一個原先的立方體透視變換後，也就是符合近大遠小的原則。

實際看來就是下面樣子

程式碼簡介

Vector4D(PointerD)，Mat(4*4矩陣)，這兩個類來進行基本數學表示，其中若用到Point2D，則採用Point4D來模擬。並附有加減乘除，向量積與數量積等運算。（基本線性代數）

Camera:

觀察相機相關，設定檢視矩陣

Transform:

包含從模型到世界到相機再到投影平面變換過程的綜合變換矩陣。

在這裡設定透視矩陣(推導參考重要矩陣部分)

Device：

綜合渲染過程。

部分系統呼叫程式碼（視窗建立，顯示framebuffer等），這一部分不必深究，因為其實它不是我們的軟渲染器的核心部分，只是輔助而已，我們只要會訪問其中的顯示快取framebuffer即可。

程式碼執行流程為：

Main {

       初始化模型mesh；

       設定windows視窗；

       例項化裝置並與視窗的顯示快取繫結；

       初始化相機。

       設定模型變換的變換矩陣的檢視矩陣與透視矩陣；

While {

       視窗相關；

       裝置顯示記憶體清空；

       裝置渲染模型；

       調整模型姿態；

       更新視窗畫面；

       Sleep(1);

}

}

Code：

All1.h

Main.cpp

PS：

之前看計算機圖形學的時候，那時感覺這一套變換流程不是很難嘛，但是今天具體實現時發現許多細節要注意。

重要矩陣

平移旋轉縮放矩陣

變換矩陣(可以是平移、旋轉、縮放矩陣或者他們的組合)

使用方式：變換矩陣 * 某一點 = 變換後的點

 

平移矩陣：

 

縮放矩陣：

x, y, z 分別表示希望x, y,z 上的縮放倍數。

 

旋轉矩陣:

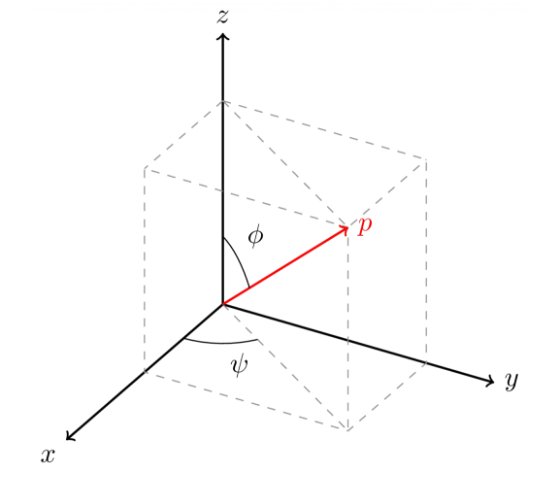
對於任意軸p時，可將旋轉分解為

1.將座標軸旋轉，使旋轉軸p與Z軸重合

2.將點w繞Z軸旋轉theta度

3.再將座標軸旋轉回原位。

即：

 

Point_after = Rz(ψ)*Ry(ϕ)*Rz(θ)*Ry(−ϕ)*Rz(−ψ)*Point_before

其中藉助旋轉矩陣作為正交矩陣的特點用 R(−α)=(R−1)(α)=RT(α)

簡化為

Rz(ψ)*Ry(ϕ)*Rz(θ)*RyT(ϕ)*RzT(ψ)

計算後可得：（x,y,z）為旋轉軸單位向量，theta為弧度制旋轉角

對一個點做變換，大部分為平移旋轉與縮放的集合，所以可以將變換矩陣利用矩陣性質組合起來，即：Mat = translation_mat * rotate_mat * scale_mat

Point_after = Mat * Point_before  (先縮放，後旋轉，然後平移)

Reference：

http://blog.csdn.net/csxiaoshui/article/details/65446125

檢視矩陣

在這裡的是

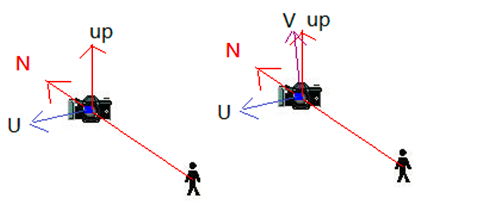
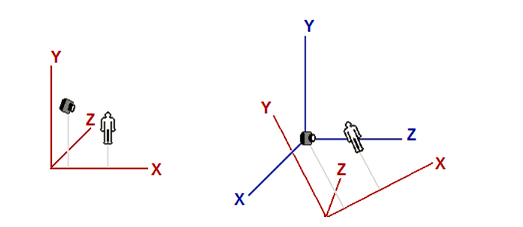
1、首先我們來求得N = eye – lookat（/*其實這裡依據左手座標系，應為lookat-eye,但因為下圖中畫出的方向一致性，這裡寫為eye –lookat，最終使用時記得換回來*/），並把N歸一化。

2、up和N差積得到U, U= up X N，歸一化U。

3、然後N和U差積得到V

 

假設一開始相機座標系和世界座標系重合，它先進行一個旋轉變化，然後再進行一個平移，得到現在是相機位置和方位。則此時進行的矩陣變化為

，其中T是平移變化，R是旋轉變化，而相機變換是相機本身變換的逆變換。

T的逆矩陣為：

當相機完成自身座標系原點移至世界座標系原點一步之後，相機的原點和世界原點就重合了，也就是處理完了關於平移的變換。

   我們要把一個世界座標系點K(Kx, Ky, Kz)，表示成(U,V,P)座標系的點（假設此時，已經經過平移操作，攝像機在世界座標系的原點），則其公式為：

Lx = Kx * Ux + Ky * Uy +Kz * Uz;

Ly = Kx * Vx + Ky * Vy +Kz * Vz;

Lz = Kx * Px + Ky * Py +Kz * Pz;

即：

Reference:

Code:

void Mat::Set_As_Rotate(float x, float y,floatz, float theta) {

    //設定為旋轉矩陣

    //theta是弧度值

    float qsin = (float)sin(theta);

    float qcos = (float)cos(theta);

    float one_qcos = 1 -qcos;

    Vector4D vi(x,y,z, 1);

    vi.Normalize();

    float X = vi.x, Y = vi.y,Z = vi.z;

    m[0][0]= qcos + X*X*one_qcos;

    m[0][1]= X*Y*one_qcos - Z*qsin;

    m[0][2]= X*Z*one_qcos + Y*qsin;

    m[0][3]= 0.0f;

    m[1][0]= Y*X*one_qcos + Z*qsin;

    m[1][1]= qcos + Y*Y*one_qcos;

    m[1][2]= Y*Z*one_qcos - X*qsin;

    m[1][3]= 0.0f;

    m[2][0]= Z*X*one_qcos - Y*qsin;

    m[2][1]= Z*Y*one_qcos + X*qsin;

    m[2][2]= qcos + Z*Z*one_qcos;

    m[2][3]= 0.0f;

    m[3][0]= 0;

    m[3][1]= 0;

    m[3][2]= 0;

    m[3][3]= 1.0f;

}

透視矩陣

說了這麼多，透視矩陣到底怎麼做的？

視錐體：

視錐體是一個三維體，他的位置和攝像機相關，視錐體的形狀決定了模型如何從camera space投影到螢幕上。最常見的投影型別-透視投影，使得離攝像機近的物體投影后較大，而離攝像機較遠的物體投影后較小。透視投影使用稜錐作為視錐體，攝像機位於稜錐的椎頂。該稜錐被前後兩個平面截斷，形成一個稜臺，叫做View Frustum，只有位於Frustum內部的模型才是可見的。

透視投影的目的：

透視投影的目的就是將上面的稜臺轉換為一個立方體（cuboid），轉換後，稜臺的前剪裁平面的右上角點變為立方體的前平面的中心（下圖中弧線所示）。由圖可知，這個變換的過程是將稜臺較小的部分放大，較大的部分縮小，以形成最終的立方體。這就是投影變換會產生近大遠小的效果的原因。變換後的x座標範圍是[-1, 1]，y座標範圍是[-1, 1]，z座標範圍是[-1, 1]。

 

透視投影矩陣推導：

那麼透視投影到底做了什麼工作呢？

我們可以將整個投影過程分為兩個部分，第一部分是從Frustum內一點投影到近剪裁平面的過程，第二部分是由近剪裁平面縮放的過程。假設Frustum內一點P（x,y,z）在近剪裁平面上的投影是P'（x',y',z'），而P'經過縮放後的最終座標設為P''(x",y",z")。假設所求的投影矩陣為M，那麼根據矩陣乘法可知，如下等式成立。

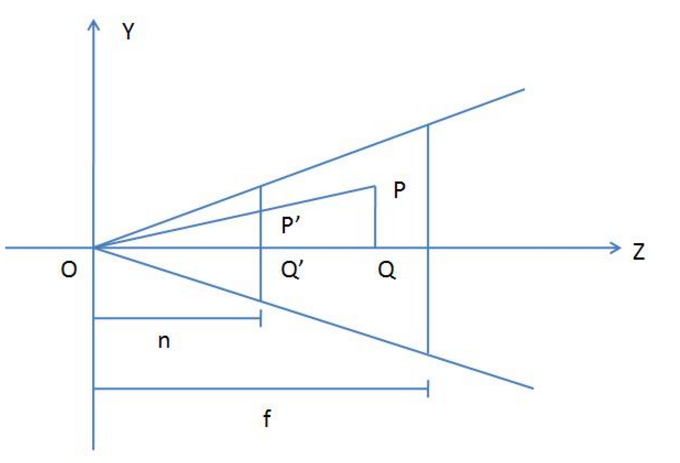
先看第一部分，為了簡化問題，我們考慮YOZ平面上的投影情況，見下圖。設P（x, y, z）是Frustum內一點，它在近剪裁平面上的投影是P'（x', y', z'）。（注意：D3D以近剪裁平面作為投影平面），設視錐體與Z軸夾角。

 由上圖可知，三角形OP'Q'與三角形OPQ相似，於是有如下等式成立。

又因為投影平面的寬長比為Aspect，所以

 即：

由W/H = Aspect

此圖問題應為除

最後看z''，當Frustum內的點投影到近剪裁平面的時候，實際上這個z'值已經沒有意義了，因為所有位於近剪裁平面上的點，其z'值都是n，看起來我們甚至可以拋棄這個z'值，可以麼？當然不行！別忘了後面還有深度測試呢。由第一幅圖可知，所有位於線段p'p上的點，最終都會投影到p'點，那麼如果這條線段上真的有多個點，如何確定最終保留哪一個呢？當然是離觀察這最近的這個了，也就是深度值（z值）最小的。所以z'座標可以直接儲存p點的z值。因為在光柵化之前，我們需要對z座標的倒數進行插值（原因請參見Mathematics for 3D Game Programming and Computer Grahpics 3rdsection 5.4），所以可以將z''寫成

 

將X”Y”Z”代入最開始矩陣乘法等式

由上式可見，x'',y'',z''都除以了Pz,於是我們將他們再乘以Pz（這並不該變齊次座標的大小），得到如下等式。

注意這裡，x即Px，y即Py，z即Pz，解矩陣的每一列得到

於是所求矩陣為

注意，這裡推得的透視變換矩陣是右乘用 即Vec_before*Mat= Vec_after

Reference：

Code:

void Transform::Init(int width, int height) {

    // 初始化，設定螢幕長寬

    world.Set_Identity();

    view.Set_Identity();

    w= (float)width;

    h= (float)height;

}

void Transform::Set_Perspective(float fovy, float aspect,floatzn, float zf) {

    //設定透視矩陣,相當於D3DXMatrixPerspectiveFovLH

    //fovy = view frustum 與Z軸夾角弧度制

    //aspect 投影面寬長比（顯示區寬長比）

    //zn 相機到近裁剪平面距離，zf相機到遠裁剪平面距離

    float fax = 1.0f / (float)tan(fovy * 0.5f);

    projection.Set_Zero();

    projection.m[0][0]= (float)(fax /aspect);

    projection.m[1][1]= (float)(fax);

    projection.m[2][2]= zf / (zf -zn);

    projection.m[2][3]= zn * zf / (zn - zf);

    projection.m[3][2]= 1;

    /*projection.m[3][2] = zn * zf / (zn - zf);

    projection.m[2][3]= 1;*/

}

void Transform::Update() {

    // 矩陣更新，計算 transform =   projection * view * world

    static Mat m;

    m.Set_Identity();

    view.Mul(world,m);

    projection.Mul(m,transform);

}

void Transform::Apply(Vector4D &op,Vector4D &re) {

    //old  將向量 op進行 project

    //此操作後，re裡的x,y即為在螢幕中顯示的位置，z留作深度測試

    transform.Mul_Vec(op, re);

}

void Transform::Homogenize(Vector4D &op,Vector4D &re) {

    // 歸一化，得到螢幕座標

    float rhw = 1.0f / op.w;

    re.x = (op.x * rhw + 1.0f) * w* 0.5f;

    re.y = (1.0f - op.y * rhw) * h *0.5f;

    re.z = op.z * rhw;

    re.w = 1.0f;

}