一、什麼是激勵函式

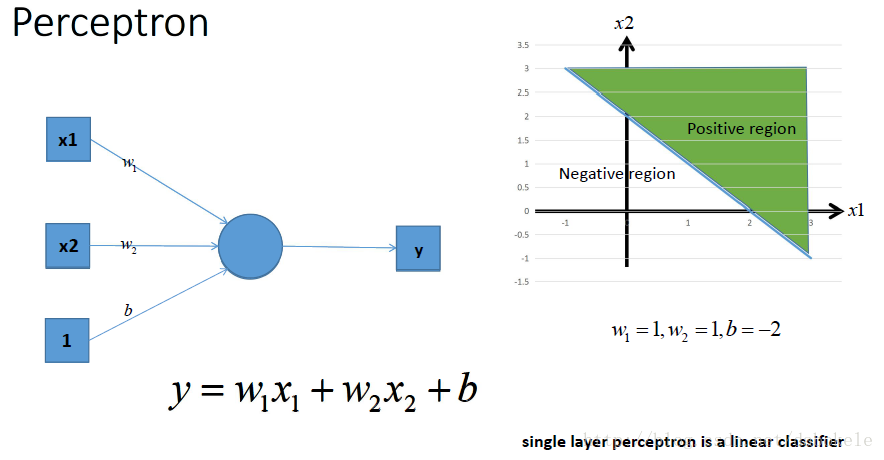
　　激勵函式一般用於神經網路的層與層之間，上一層的輸出通過激勵函式的轉換之後輸入到下一層中。神經網路模型是非線性的，如果沒有使用激勵函式，那麼每一層實際上都相當於矩陣相乘。經過非線性的激勵函式作用，使得神經網路有了更多的表現力。

　　為了更具體的描述這個問題，請參考知乎上的回答。

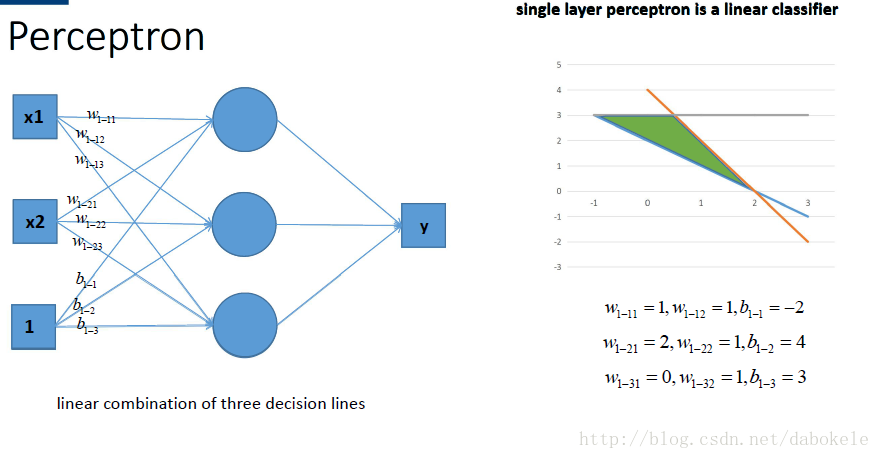
那麼很容易地我們就會想用多個感知機來進行組合, 獲得更強的分類能力, 這是沒問題的啦~~
如圖所示,

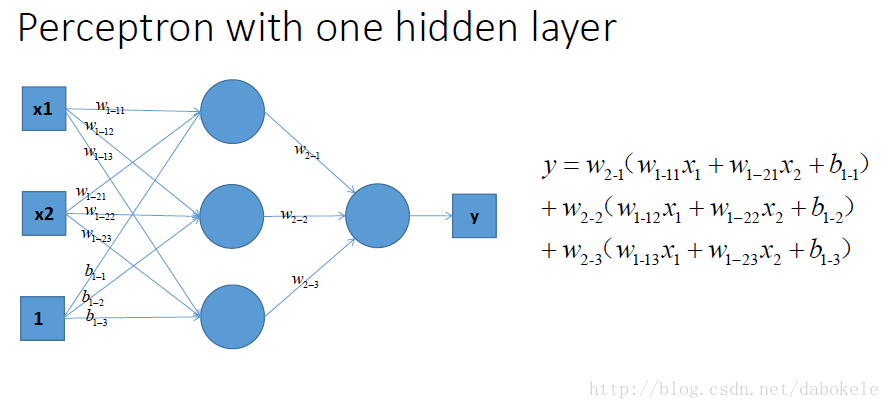
那麼我們動筆算一算, 就可以發現, 這樣一個神經網路組合起來,輸出的時候無論如何都還是一個線性方程哎~納尼, 說好的非線性分類呢~!!!!???

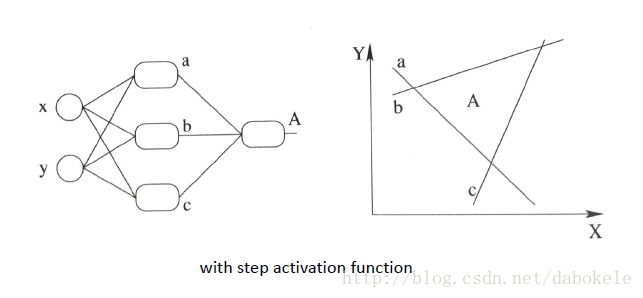
再盜用一幅經常在課堂上用的圖…然而我已經不知道出處是哪了, 好像好多老師都是直接用的, 那我就不客氣了嘿嘿嘿~，這幅圖就跟前面的圖一樣, 描述了當我們直接使用step activation function的時候所能獲得的分類器, 其實只能還是線性的, 最多不過是複雜的線性組合罷了，當然你可以說我們可以用無限條直線去逼近一條曲線啊……額,當然可以, 不過比起用non-linear的activation function來說就太傻了嘛….

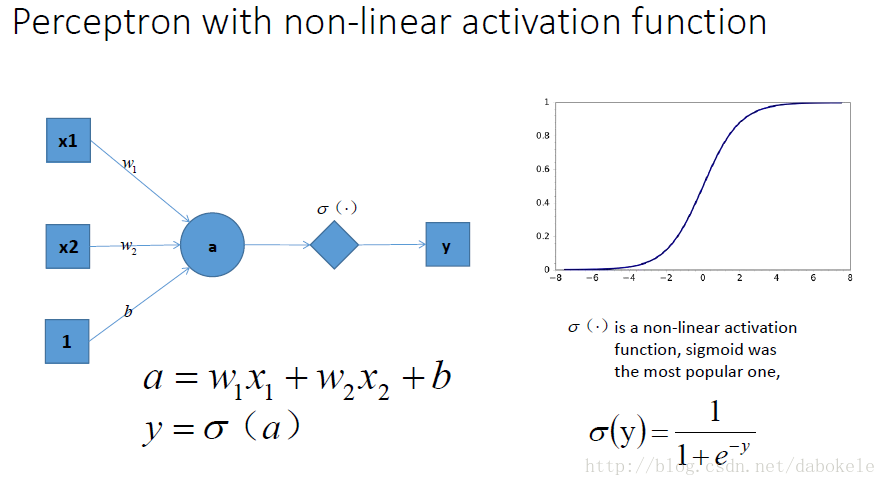
祭出主菜. 題主問的激勵函式作用是什麼, 就在這裡了!!
我們在每一層疊加完了以後, 加一個啟用函式, 如圖中的y

=δ(a). 這樣輸出的就是一個不折不扣的非線性函式!

於是就很容易拓展到多層的情況啦, 更剛剛一樣的結構, 加上non-linear activation function之後, 輸出就變成了一個複雜的, 複雜的, 超級複雜的函式….額別問我他會長成什麼樣, 沒人知道的~我們只能說, 有了這樣的非線性啟用函式以後, 神經網路的表達能力更加強大了~(比起純線性組合, 那是必須得啊!)

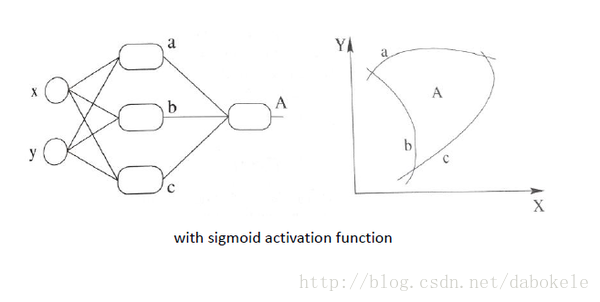
繼續厚顏無恥地放一張跟之前那副圖並列的圖, 加上非線性啟用函式之後, 我們就有可能學習到這樣的平滑分類平面. 這個比剛剛那個看起來牛逼多了有木有!

二、不同激勵函式的公式和圖形

1、Sigmoid函式
　　Sigmoid函式公式如下

δ(x)=11+e−x
　　函式圖形如下：
　　
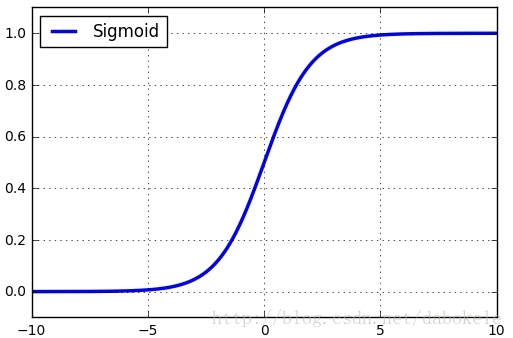
　　觀察函式圖形可以看到，Sigmoid函式將輸入值歸一化到(0, 1)之間。
　　
　　Sigmoid函式導數公式如下
dδ(x)dx=ex(1+ex)2
　　函式圖形如下：
　　

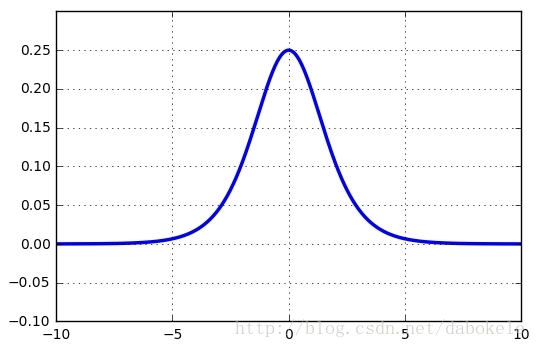
　　Sigmoid函式有三個缺點：　　
（1）Saturated neurons “kill” the gradients
　　在一些誤差反向傳播的場景下。首先會計算輸出層的loss，然後將該loss以導數的形式不斷向上一層神經網路傳遞，調整引數。使用Sigmoid函式的話，很容易導致loss導數變為0，從而失去優化引數的功能。
　　並且Sigmoid函式的導數最大值為0.25，該誤差經過多層神經網路後，會快速衰減到0。
　　
（2）Sigmoid outputs are not zero-centered
　　Sigmoid函式的輸出值恆大於零，那麼下一層神經網路的輸入x恆大於零。
　　

f=wTx+b
　　對上面這個公式來說，w上的gradient將會全部大於零或者全部小於零。這會導致模型訓練的收斂速度變慢。
　　如下圖所示，當輸入值均為正數時，會導致按紅色箭頭所示的階梯式更新。
　　
　　

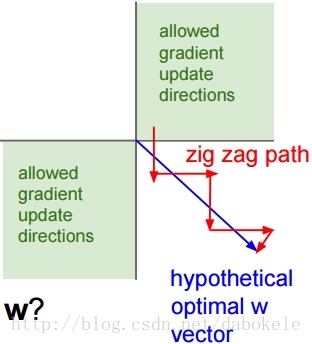
（3）exp() is a bit compute expensive
　　最後，Sigmoid函式中的指數運算也是一個比較消耗計算資源的過程。
　　
2、Tanh函式

　　接下來的Tanh函式基於Sigmoid函式進行了一些優化，克服了Sigmoid的not zero-centered的缺點。Tanh函式公式如下：　　

tanh(x)=ex−e−xex+e−x

　　Sigmoid函式和Tanh函式之間的關係如下：

tanh(x)=2δ(2x)−1
　　
　　所以，對應於sigmoid的取值範圍(0, 1)，tanh的取值範圍為(0, 1)。將兩個函式影象畫在同一座標系中，如下圖所示：
　　

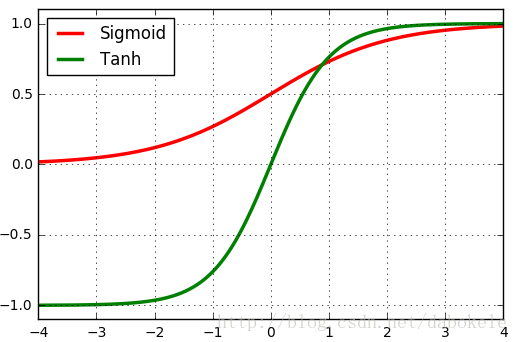
　　所以Tanh仍然具有Sigmoid函式的另外兩個不足。
　　
3、ReLU函式
　　ReLU函式公式如下所示：

ReLU=max(0,x)

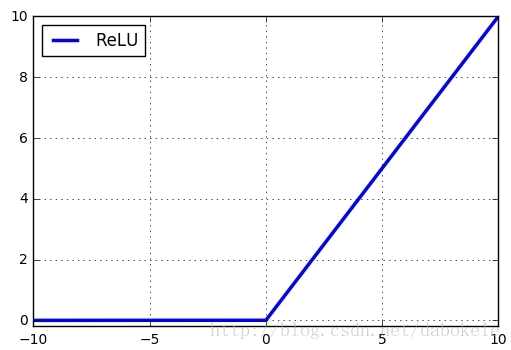
　　對應函式圖形如下：
　　

　　該函式在輸入小於0時輸出值恆為0，在輸入大於0時，輸出線性增長。

　　ReLU函式沒有Sigmoid函式及Tanh函式中的指數運算，並且也沒有”kill” gradients的現象。
　　但是ReLU函式也有以下幾個不足之處：
（1）not zero-centered
　　這個與Sigmoid類似，從函式圖形就可以看出。
　　
（2）dead relu
　　這裡指的是某些神經元可能永遠不會被啟用，導致對應的引數永遠不會被更新。
　　比如說一個非常大的Gradient流過ReLU神經元，可能會導致引數更新後該神經元再也不會被啟用。
　　當學習率過大時，可能會導致大部分神經元出現dead狀況。所以使用該啟用函式時應該避免學習率設定的過大。另外一種比較少見的情況是，某些初始化引數也會導致一些神經元出現dead狀況。

４、Softplus函式

　　Softplus函式公式如下，

Softplus(x)=log(1+ex)
　　通過觀察該公式可以發現Softplus函式是Sigmoid函式的原函式。

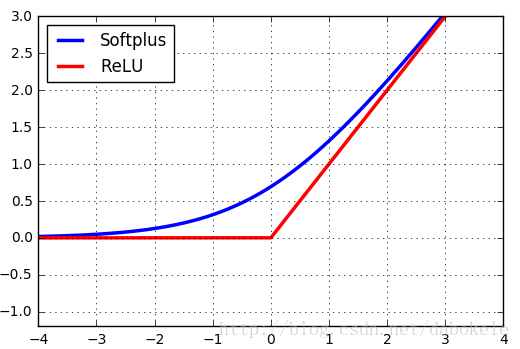
　　Softplus函式與ReLU函式的圖形對比如下圖所示，
　　

　　在這裡之所以將Softplus函式與ReLU函式的圖形放在一起進行比較，是因為Softplus函式可以看成是ReLU函式的平滑版本。
　　並且，Softplus函式是對全部資料進行了非線性對映，是一種不飽和的非線性函式其表示式如公式，Softplus函式不具備稀疏表達的能力，收斂速度比ReLUs函式要慢很多。但該函式連續可微並且變化平緩，比Sigmoid函式更加接近生物學的啟用特性，同時解決了Sigmoid函式的假飽和現象，易於網路訓練和泛化效能的提高。雖然該函式的表達效能更優於ReLU函式和Sigmoid函式，即精確度相對於後者有所提高，但是其並沒有加速神經網路的學習速度。
　　
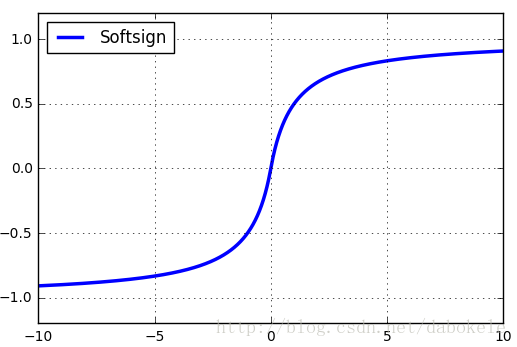
５、Softsign函式
softsign(x)=11+|x|

　　

三、Tensorflow中提供的激勵函式

　　在Tensorflow r1.0中提供了以下幾種激勵函式，其中包括連續非線性的（比如sigmoid, tanh, elu, softplus, softsign），連續但是並不是處處可微分的（relu, relu6, crelu, relu_x）以及隨機函式（dropout）。

tf.nn.relu
tf.nn.relu6
tf.nn.crelu
tf.nn.elu
tf.nn.softplus
tf.nn.softsign
tf.nn.dropout
tf.nn.bias_add
tf.sigmoid
tf.tanh