最近把向量乘法運算搞混了，故而溫習一下。

內容主要來自以下兩個文件

0. 綜述

常用的,

• a·b=||a||||b||cosθ, 這個是向量的內積，又叫數量積，又叫點積。
• axb = ||a||||b||sinθ，這個是向量的外積，又叫向量積，又叫叉積。
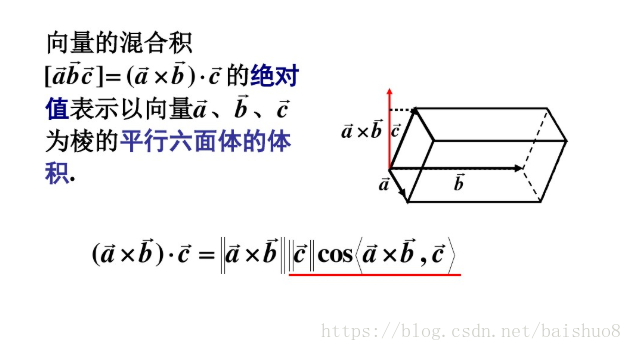
• [a b c] =(axb)·c , 這個是向量的混合積。

1. 內積

1.1 定義

1.2 向量內積性質

注意，向量內積不滿足結合律，即一般情況下 (a·b)·c != a·(b·c), 因為向量的內積結果是一個標量。

1.3 向量內積的物理意義

向量內積的物理意義是，力通過位移做功。

1.4 向量內積的用途

1.4.1 求兩個非零向量的夾角 

1.4.2 判斷兩個非零向量是否垂直

簡單的對應座標相乘再求和，結果為0就垂直，否則就不垂直。

2. 外積

2.1 向量外積的定義

向量外積的結果是垂直於原向量所定義平面的向量。

通過座標進行外積的直接計算比較複雜，寫成行列式的形式，再展開，方便記憶。

2.2 向量外積的性質

2.3 向量外積的幾何意義

再除以2的話，就是以 a，b 為邊的三角形的面積。

2.4 向量外積的用途

2.4.1 求與三角形面積相關的問題

3. 混合積

3.1 向量混合積的定義

三個向量，先外積後內積，最後出個標量結果，就是三個向量的混合積。

混合積的座標表示式非常規整優美。

3.2 混合積的性質

3.3 混合積的幾何意義

3.4 混合積的用途

3.4.1 求四面體體積相關

3.4.2 判斷三個向量共面