前面一篇文章《異常點檢測演算法（一）》簡要的介紹瞭如何使用概率統計的方法來計算異常點，本文將會介紹一種基於矩陣分解的異常點檢測方法。在介紹這種方法之前，先回顧一下主成分分析（Principle Component Analysis）這一基本的降維方法。

（一）主成分分析（Principle Component Analysis）

對高維資料集合的簡化有各種各樣的原因，例如：

（1）使得資料集合更容易使用；

（2）降低很多演算法的計算開銷；

（3）去除噪聲；

（4）更加容易的描述結果。

在主成分分析（PCA）這種降維方法中，資料從原來的座標系轉換到新的座標系，新座標系的選擇是由資料集本身所決定的。第一個新座標軸的方向選擇的是原始資料集中方差最大的方向，第二個新座標軸的選擇是和第一個座標軸正交併且具有最大方差的方向。該過程一直重複，重複的次數就是原始資料中特徵的數目。如此操作下去，將會發現，大部分方差都包含在最前面的幾個新座標軸之中。因此，我們可以忽略餘下的座標軸，也就是對資料進行了降維的處理。

為了提取到第一個主成分（資料差異性最大）的方向，進而提取到第二個主成分（資料差異性次大）的方向，並且該方向需要和第一個主成分方向正交，那麼我們就需要對資料集的協方差矩陣進行特徵值的分析，從而獲得這些主成分的方向。一旦我們計算出了協方差矩陣的特徵向量，我們就可以保留最大的 N 個值。正是這 N 個值反映了 N 個最重要特徵的真實資訊，可以把原始資料集合對映到 N 維的低維空間。

提取 N 個主成分的虛擬碼如下：

去除平均值

計算協方差矩陣

計算協方差矩陣的特徵值和特徵向量

將特徵值從大到小排序

保留最大的N個特徵值以及它們的特徵向量

將資料對映到上述N個特徵向量構造的新空間中

通過 Python 的 numpy 庫和 matplotlib 庫可以計算出某個二維資料集合的第一主成分如下：原始資料集使用藍色的三角形表示，第一主成分使用黃色的圓點表示。

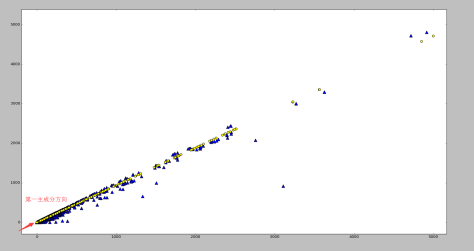
Principle Component Analysis 的基本性質：

Principle component analysis provides a set of eigenvectors satisfying the following properties:

（1）If the top-k eigenvectors are picked (by largest eigenvalue), then the k-dimensional hyperplane defined by these eigenvectors, and passing through the mean of the data, is a plane for which the mean square distance of all data points to it is as small as possible among all hyperplanes of dimensionality k.

（2）If the data is transformed to the axis-system corresponding to the orthogonal eigenvectors, the variance of the transformed data along each eigenvector dimension is equal to the corresponding eigenvalue. The covariances of the transformed data in this new representation are 0.

（3）Since the variances of the transformed data along the eigenvectors with small eigenvalues are low, significant deviations of the transformed data from the mean values along these directions may representoutliers.

（二）基於矩陣分解的異常點檢測方法

基於矩陣分解的異常點檢測方法的關鍵思想是利用主成分分析去尋找那些違背了資料之間相關性的異常點。為了發現這些異常點，基於主成分分析（PCA）的演算法會把原始資料從原始的空間投影到主成分空間，然後再把投影拉回到原始的空間。如果只使用第一主成分來進行投影和重構，對於大多數的資料而言，重構之後的誤差是小的；但是對於異常點而言，重構之後的誤差依然相對大。這是因為第一主成分反映了正常值的方差，最後一個主成分反映了異常點的方差。

假設 dataMat 是一個 p 維的資料集合，有 N 個樣本，它的協方差矩陣是 X。那麼協方差矩陣就通過奇異值分解寫成：

其中 P 是一個 (p,p) 維的正交矩陣，它的每一列都是 X 的特徵向量。D 是一個 (p,p) 維的對角矩陣，包含了特徵值 。從影象上看，一個特徵向量可以看成 2 維平面上面的一條線，或者高維空間裡面的一個超平面。特徵向量所對應的特徵值反映了這批資料在這個方向上的拉伸程度。通常情況下，可以把對角矩陣 D 中的特徵值進行從大到小的排序，矩陣 P 的每一列也進行相應的調整，保證 P 的第 i 列對應的是 D 的第 i 個對角值。

這個資料集 dataMat 在主成分空間的投影可以寫成

需要注意的是做投影可以只在部分的維度上進行，如果使用 top-j 的主成分的話，那麼投影之後的資料集是

其中 是矩陣 P 的前 j 列，也就是說 是一個 (p,j) 維的矩陣， 是一個 (N,j) 維的矩陣。如果考慮拉回對映的話（也就是從主成分空間對映到原始空間），重構之後的資料集合是

其中 是使用 top-j 的主成分進行重構之後形成的資料集，是一個 (N,p) 維的矩陣。

下面可以定義資料 的異常值分數（outlier score）如下：

注意到 指的是 Euclidean 範數， ev(j) 表示的是 top-j 的主成分在所有主成分中所佔的比例，並且特徵值是按照從大到小的順序排列的。因此，ev(j) 是遞增的序列，這就表示 j 越高，越多的方差就會被考慮在 ev(j) 中，因為是從 1 到 j 的求和。在這個定義下，偏差最大的第一個主成分獲得最小的權重，偏差最小的最後一個主成分獲得了最大的權重 1。根據 PCA 的性質，異常點在最後一個主成分上有著較大的偏差，因此可以獲得更高的分數。

整個演算法的結構如圖所示：

（三）效果展示

下面兩幅圖使用了同一批資料集，分別採用了基於矩陣分解的異常點檢測演算法和基於高斯分佈的概率模型的異常點演算法。

基於矩陣分解的異常點檢測

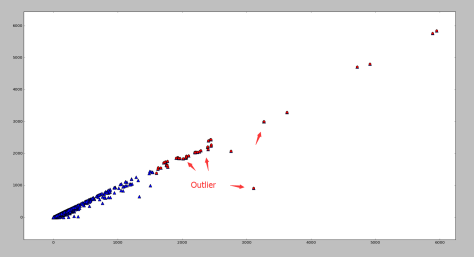
基於高斯分佈的概率模型的異常點檢測

根據影象可以看出，如果使用基於矩陣分解的異常點檢測演算法的話，偏離第一主成分較多的點都被標記為異常點，其中包括部分左下角的點。需要注意的是如果使用基於高斯分佈的概率模型的話，是不太可能標記出左下角的點的，兩者形成鮮明對比。

原文地址:https://zr9558.com/2016/06/23/outlierdetectiontwo/