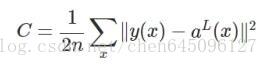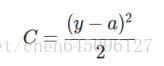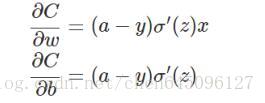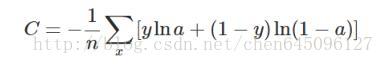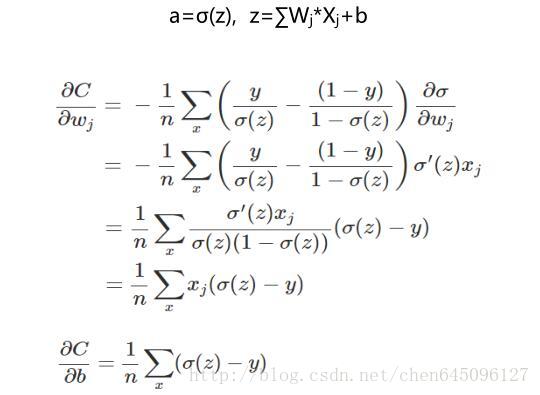深度學習中常用的代價函式
1.二次代價函式(quadratic cost):
其中,C表示代價函式,x表示樣本,y表示實際值,a表示輸出值,n表示樣本的總數。為簡單起見,使用一個樣
本為例進行說明,此時二次代價函式為:
假如我們使用梯度下降法(Gradient descent)來調整權值引數的大小,權值w和偏置b的梯度推導如下:
其中,z表示神經元的輸入,σ表示啟用函式。w和b的梯度跟啟用函式的梯度成正比,啟用函式的梯度越大,w
和b的大小調整得越快,訓練收斂得就越快。假設我們的啟用函式是sigmoid函式:
假設我們目標是收斂到1.0。1點為0.82離目標比較遠,梯度比較大,權值調整比較大。2點為0.98離目標比較近,梯度比較小,權值調整比較小。調整方案合理。
假如我們目標是收斂到0。1點為0.82目標比較近,梯度比較大,權值調整比較大。2點為0.98離目標比較遠,梯
度比較小,權值調整比較小。調整方案不合理。
2.交叉熵代價函式(cross-entropy):
換一個思路,我們不改變啟用函式,而是改變代價函式,改用交叉熵代價函式:
其中,C表示代價函式,x表示樣本,y表示實際值,a表示輸出值,n表示樣本的總數。
當誤差越大時,梯度就越大,引數w和b的調整就越快,訓練的速度也就越快。
如果輸出神經元是線性的,那麼二次代價函式就是一種合適的選擇。如果輸出神經元是S型函式,那麼比較適合
用交叉熵代價函式。
3.對數釋然代價函式(log-likelihood cost):
對數釋然函式常用來作為softmax迴歸的代價函式,然後輸出層神經元是sigmoid函式,可以採用交叉熵代價函
數。而深度學習中更普遍的做法是將softmax作為最後一層,此時常用的代價函式是對數釋然代價函式。
對數似然代價函式與softmax的組合和交叉熵與sigmoid函式的組合非常相似。對數釋然代價函式在二分類時可
以化簡為交叉熵代價函式的形式。
4.總結:
在tensorflow中用:
tf.nn.sigmoid_cross_entropy_with_logits()來表示跟sigmoid搭配使用的交叉熵。
tf.nn.softmax_cross_entropy_with_logits()來表示跟softmax搭配使用的交叉熵。