稀疏矩陣的行壓縮儲存(CSR/CRS), 列壓縮儲存CCS
轉載地址:http://blog.csdn.net/bigpiglet_zju/article/details/20791881
稀疏矩陣(Sparse Matrix)由於有很多0,為了節省空間,一般壓縮儲存。通常只需要儲存非零元素及其位置即可。
下面介紹Compressed Row Storage(CRS)格式或者稱為 Compressed sparse row(CSR)格式,由名稱可見,該格式是把行的資訊壓縮儲存了,只顯式保留每行第一個非零元素的位置,具體在例子中可以看到。
假設有稀疏矩陣A,我們需要建立三個陣列,一個浮點型陣列val,另外兩個為整型陣列(col_ind, row_ptr)。
val陣列,大小為矩陣A的非零元素的個數,儲存矩陣A的非零元素(按從上往下,從左往右的行遍歷方式訪問元素)。
如果val(k)=a(i,j),則col_ind(k)=j。col_ind陣列,和val陣列一樣,大小為矩陣A的非零元素的個數,儲存val陣列中元素的列索引。其數學表示為:
如果val(k)=a(i,j),則row_ptr(i)<= k < row_ptr(i+1)。row_ptr陣列,大小為矩陣A的行數,儲存矩陣A的每行第一個非零元素在val中的索引。其數學表示為:
按照慣例,一般定義row_ptr(n+1) = nnz + 1
,而nnz是A中非零元素的個數。
該方法可以節省很多空間,只需要2nnz + n + 1個儲存單元,而不是n的平方個單元。
//ps:這的n好像指的是:方陣的行/列
看一個例子:
矩陣A定義為
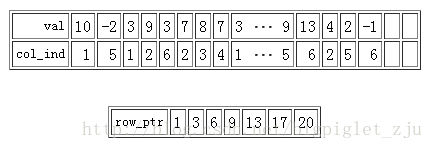
其CSR格式由三個陣列定義為:
注意其中row_ptr陣列的最後一個元素為20(19+1),因為矩陣A的非零元素為19。
Compressed Column Storage
Analogous to CRS, there is compressed column storage (CCS), which is also called the Harwell-Boeing
The CCS format is specified by the ![]() arrays {val, row_ind, col_ptr},
where row_ind stores the row indices of each nonzero, and col_ptr stores the index of the elements in val which start a column of
arrays {val, row_ind, col_ptr},
where row_ind stores the row indices of each nonzero, and col_ptr stores the index of the elements in val which start a column of ![]() .
The CCS format for the matrix
.
The CCS format for the matrix ![]() in (10.1)
is given by
in (10.1)
is given by
| val | 10 | 3 | 3 | 9 | 7 | 8 | 4 | 8 | 8 |
2 | 3 | 13 | -1 |
| row_ind | 1 | 2 | 4 | 2 | 3 | 5 | 6 | 3 | 4 |
6 | 2 | 5 | 6 |
| col_ptr | 1 | 4 | 8 | 10 | 13 | 17 | 20 |
2. Compressed Column Storage
http://www.netlib.org/utk/people/JackDongarra/etemplates/node374.html