http://www.cnblogs.com/xbinworld/p/4273506.html?utm_source=tuicool&utm_medium=referral

稀疏矩陣是指矩陣中的元素大部分是0的矩陣，事實上，實際問題中大規模矩陣基本上都是稀疏矩陣，很多稀疏度在90%甚至99%以上。因此我們需要有高效的稀疏矩陣儲存格式。本文總結幾種典型的格式：COO,CSR,DIA,ELL,HYB。

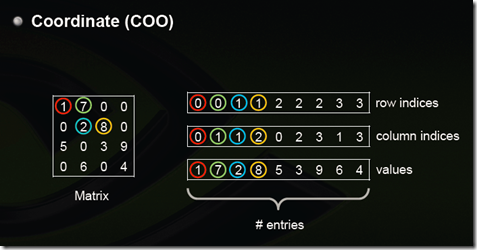
（1）Coordinate（COO）

這是最簡單的一種格式，每一個元素需要用一個三元組來表示，分別是（行號，列號，數值），對應上圖右邊的一列。這種方式簡單，但是記錄單資訊多（行列），每個三元組自己可以定位，因此空間不是最優。

（2）Compressed Sparse Row (CSR)

CSR是比較標準的一種，也需要三類資料來表達：數值，列號，以及行偏移。CSR不是三元組，而是整體的編碼方式。數值和列號與COO一致，表示一個元素以及其列號，行偏移表示某一行的第一個元素在values裡面的起始偏移位置。如上圖中，第一行元素1是0偏移，第二行元素2是2偏移，第三行元素5是4偏移，第4行元素6是7偏移。在行偏移的最後補上矩陣總的元素個數，本例中是9。

CSC是和CSR相對應的一種方式，即按列壓縮的意思。

以上圖中矩陣為例：

Values：        [1 5 7 2 6 8 3 9 4]

Row Indices：[0 2 0 1 3 1 2 2 3]

Column Offsets：[0 2 5 7 9]

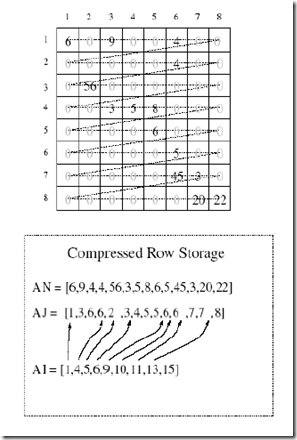
再來看一個CSR的例子[4]：

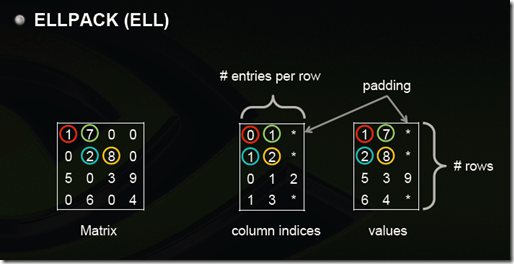
（3）ELLPACK (ELL)

用兩個和原始矩陣相同行數的矩陣來存：第一個矩陣存的是列號，第二個矩陣存的是數值，行號就不存了，用自身所在的行來表示；這兩個矩陣每一行都是從頭開始放，如果沒有元素了就用個標誌比如*結束。上圖中間矩陣有誤，第三行應該是  0 2 3。

注：這樣如果某一行很多元素，那麼後面兩個矩陣就會很胖，其他行結尾*很多，浪費。可以存成陣列，比如上面兩個矩陣就是：

0 1 * 1 2 * 0 2 3 * 1 3 *

1 7 * 2 8 * 5 3 9 * 6 4 *

但是這樣要取一行就比較不方便了

（4）Diagonal (DIA)

對角線儲存法，按對角線方式存，列代表對角線，行代表行。省略全零的對角線。(從左下往右上開始：第一個對角線是零忽略，第二個對角線是5，6，第三個對角線是零忽略，第四個對角線是1，2，3，4，第五個對角線是7，8，9，第六第七個對角線忽略)。[3]

這裡行對應行，所以5和6是分別在第三行第四行的，前面補上無效元素*。如果對角線中間有0，存的時候也需要補0，所以如果原始矩陣就是一個對角性很好的矩陣那壓縮率會非常高，比如下圖，但是如果是隨機的那效率會非常糟糕。

（5）Hybrid (HYB) ELL + COO

為了解決（3）ELL中提到的，如果某一行特別多，造成其他行的浪費，那麼把這些多出來的元素（比如第三行的9，其他每一行最大都是2個元素）用COO單獨儲存。

選擇稀疏矩陣儲存格式的一些經驗[2]：

1. DIA和ELL格式在進行稀疏矩陣-向量乘積(sparse matrix-vector products)時效率最高，所以它們是應用迭代法(如共軛梯度法)解稀疏線性系統最快的格式；
2. COO和CSR格式比起DIA和ELL來，更加靈活，易於操作；
3. ELL的優點是快速，而COO優點是靈活，二者結合後的HYB格式是一種不錯的稀疏矩陣表示格式；
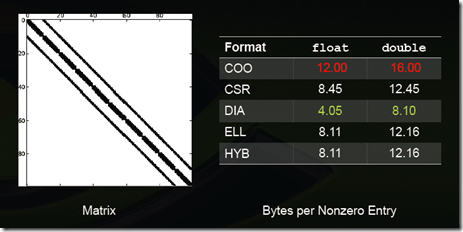
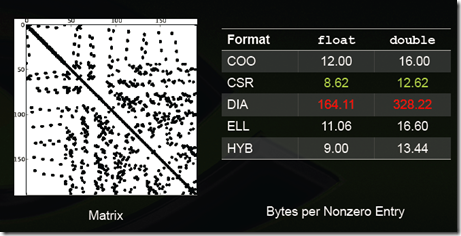
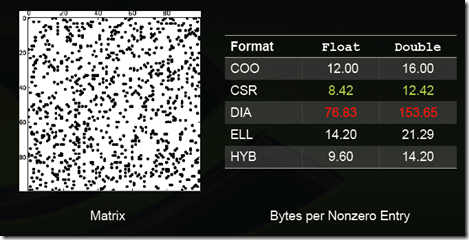
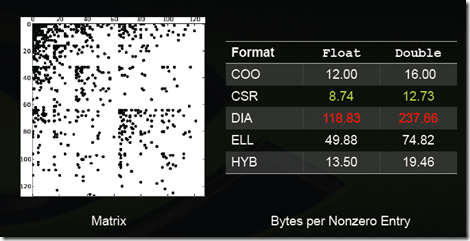
4. 根據Nathan Bell的工作，CSR格式在儲存稀疏矩陣時非零元素平均使用的位元組數(Bytes per Nonzero Entry)最為穩定（float型別約為8.5，double型別約為12.5），而DIA格式儲存資料的非零元素平均使用的位元組數與矩陣型別有較大關係，適合於StructuredMesh結構的稀疏矩陣（float型別約為4.05，double型別約為8.10），對於Unstructured Mesh以及Random Matrix,DIA格式使用的位元組數是CSR格式的十幾倍；
5. 從我使用過的一些線性代數計算庫來說，COO格式常用於從檔案中進行稀疏矩陣的讀寫，如matrix market即採用COO格式，而CSR格式常用於讀入資料後進行稀疏矩陣計算。

一些特殊型別矩陣的儲存效率（數值越小說明壓縮率越高，即儲存效率越高）:

Structured Mesh

Unstructured Mesh

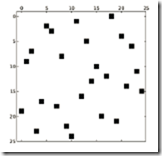
Random matrix

Power-Law Graph

格式適用性總結：

下面摘自[2]

6. Skyline Storage Format

The skyline storage format is important for the direct sparse solvers, and it is well suited for Cholesky or LU decomposition when no pivoting is required.

The skyline storage format accepted in Intel MKL can store only triangular matrix or triangular part of a matrix. This format is specified by two arrays:valuesandpointers. The following table describes these arrays:

values

A scalar array. For a lower triangular matrix it contains the set of elements from each row of the matrix starting from the first non-zero element to and including the diagonal element. For an upper triangular matrix it contains the set of elements from each column of the matrix starting with the first non-zero element down to and including the diagonal element. Encountered zero elements are included in the sets.

pointers

An integer array with dimension(m+1), wheremis the number of rows for lower triangle (columns for the upper triangle).pointers(i) -pointers(1)+1gives the index of element invaluesthat is first non-zero element in row (column)i. The value ofpointers(m+1)is set tonnz+pointers(1), wherennzis the number of elements in the arrayvalues.

7. Block Compressed Sparse Row Format (BSR)

The Intel MKL block compressed sparse row (BSR) format for sparse matrices is specified by four arrays:values,columns,pointerB, andpointerE. The following table describes these arrays.

values

A real array that contains the elements of the non-zero blocks of a sparse matrix. The elements are stored block-by-block in row-major order. A non-zero block is the block that contains at least one non-zero element. All elements of non-zero blocks are stored, even if some of them is equal to zero. Within each non-zero block elements are stored in column-major order in the case of one-based indexing, and in row-major order in the case of the zero-based indexing.

columns

Elementiof the integer arraycolumnsis the number of the column in the block matrix that contains thei-th non-zero block.

pointerB

Elementjof this integer array gives the index of the element in thecolumnsarray that is first non-zero block in a rowjof the block matrix.

pointerE

Elementjof this integer array gives the index of the element in thecolumnsarray that contains the last non-zero block in a rowjof the block matrix plus 1.

[5] Implementing Sparse Matrix-Vector Multiplication on Throughput-Oriented Processors, Nathan Bell and Michael Garland, Proceedings of Supercomputing '09

[6] Efficient Sparse Matrix-Vector Multiplication on CUDA, Nathan Bell and Michael Garland, NVIDIA Technical Report NVR-2008-004, December 2008