—— 原文釋出於本人的微信公眾號“大資料與人工智慧Lab”（BigdataAILab），歡迎關注。

讓我們把時間撥回到2006年以前，神經網路自20世紀50年代發展起來後，因其良好的非線效能力、泛化能力而備受關注。然而，傳統的神經網路仍存在一些侷限，在上個世紀90年代陷入衰落，主要有以下幾個原因：
1、傳統的神經網路一般都是單隱層，最多兩個隱層，因為一旦神經元個數太多、隱層太多，模型的引數數量迅速增長，模型訓練的時間非常之久；
2、傳統的神經網路，隨著層數的增加，採用隨機梯度下降的話一般很難找到最優解，容易陷入區域性最優解。在反向傳播過程中也容易出現梯度彌散或梯度飽和的情況，導致模型結果不理想；
3、隨著神經網路層數的增加，深度神經網路的模型引數很多，就要求在訓練時需要有很大的標籤資料，因為訓練資料少的時候很難找到最優解，也就是說深度神經網路不具備解決小樣本問題的能力。

由於以上的限制，深度的神經網路一度被認為是無法訓練的，從而使神經網路的發展一度停滯不前。

2006年，“神經網路之父”Geoffrey Hinton祭出神器，一舉解決了深層神經網路的訓練問題，推動了深度學習的快速發展，開創了人工智慧的新局面，使近幾年來科技界湧現出了很多智慧化產品，深深地影響了我們每個人的生活。

那這個神器是什麼呢？那就是“深度信念網路”（Deep Belief Network，簡稱DBN）。

深度信念網路（DBN）通過採用逐層訓練的方式，解決了深層次神經網路的優化問題，通過逐層訓練為整個網路賦予了較好的初始權值，使得網路只要經過微調就可以達到最優解。而在逐層訓練的時候起到最重要作用的是“受限玻爾茲曼機”（Restricted Boltzmann Machines，簡稱RBM）

一、玻爾茲曼機（Boltzmann Machines，簡稱BM）
 
玻爾茲曼機於1986年由大神Hinton提出，是一種根植於統計力學的隨機神經網路，這種網路中神經元只有兩種狀態（未啟用、啟用），用二進位制0、1表示，狀態的取值根據概率統計法則決定。
由於這種概率統計法則的表達形式與著名統計力學家L.E.Boltzmann提出的玻爾茲曼分佈類似，故將這種網路取名為“玻爾茲曼機”。
在物理學上，玻爾茲曼分佈（也稱為吉布斯分佈，Gibbs Distribution）是描述理想氣體在受保守外力的作用（或保守外力的作用不可忽略）時，處於熱平衡態下的氣體分子按能量的分佈規律。
在統計學習中，如果我們將需要學習的模型看成高溫物體，將學習的過程看成一個降溫達到熱平衡的過程（熱平衡在物理學領域通常指溫度在時間或空間上的穩定），最終模型的能量將會收斂為一個分佈，在全域性極小能量上下波動，這個過程稱為“模擬退火”，其名字來自冶金學的專有名詞“退火”，即將材料加熱後再以一定的速度退火冷卻，可以減少晶格中的缺陷，而模型能量收斂到的分佈即為玻爾茲曼分佈。
聽起來很難理解的樣子，只需要記住一個關鍵點：能量收斂到最小後，熱平衡趨於穩定，也就是說，在能量最少的時候，網路最穩定，此時網路最優。

玻爾茲曼機（BM）是由隨機神經元全連線組成的反饋神經網路，且對稱連線，由可見層、隱層組成，BM可以看做是一個無向圖，如下圖所示：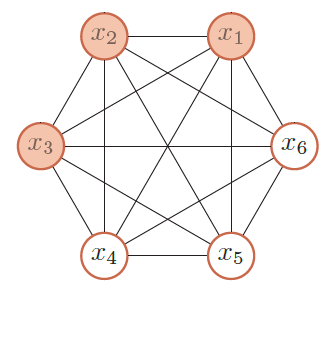
 
其中，x1、x2、x3為可見層，x4、x5、x6為隱層。
整個能量函式定義為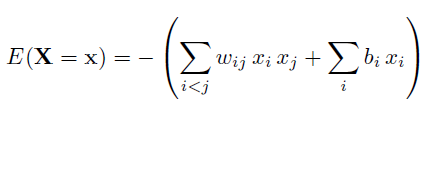
 
其中，w為權重，b為偏置變數，x只有{0,1}兩種狀態。
根據玻爾茲曼分佈，給出的一個系統在特定狀態能量和系統溫度下的概率分佈，如下：
 
前面講過，“能量收斂到最小後，熱平衡趨於穩定”，因此：
1、簡單粗暴法
要尋找一個變數使得整個網路的能量最小，一個簡單（但是低效）的做法是選擇一個變數，在其它變數保持不變的情況下，將這個變數設為會導致整個網路能量更低的狀態。那麼一個變數Xi的兩個狀態0（關閉）和1（開啟）之間的能量差異為：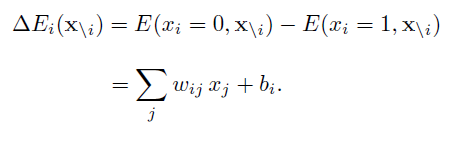
 
這時，如果能量差異ΔE大於一定的閾值（比如0），我們就設Xi = 1（也即取能量小的），否則就設Xi = 0。這種簡單的方法通過反覆不斷執行，在一定時間之後收斂到一個解（可能是區域性最優解）。
2、最大似然法
利用“模擬退火”原理尋找全域性最優解，根據玻爾茲曼分佈，Xi=1的概率為：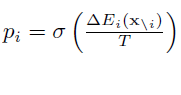
 
訓練集v的對數似然函式為：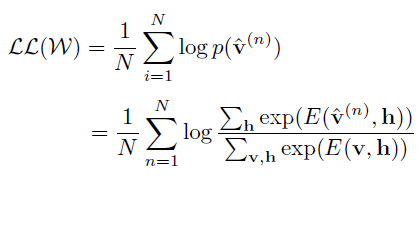
 
對每個訓練向量p(v)的對數似然對引數w求導數，得到梯度：
 
跟傳統的神經網路類似，引數w的更新公式如下（a為學習率）：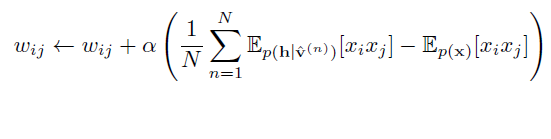
     
好了好了，公式就講到這裡了，看上去挺複雜的，沒錯，確實計算很複雜，這個梯度很難精確計算，整個計算過程會十分地耗時。
目前，可以通過一些取樣方法（例如Gibbs取樣）來進行近似求解。

玻爾茲曼機（BM）可以用在監督學習和無監督學習中。在監督學習中，可見變數又可以分為輸入和輸出變數，隱變數則隱式地描述了可見變數之間複雜的約束關係。在無監督學習中，隱變數可以看做是可見變數的內部特徵表示，能夠學習資料中複雜的規則。玻爾茲曼機代價是訓練時間很長很長很長。

二、受限玻爾茲曼機（Restricted Boltzmann Machines，簡稱RBM）
 
所謂“受限玻爾茲曼機”（RBM）就是對“玻爾茲曼機”（BM）進行簡化，使玻爾茲曼機更容易更加簡單使用，原本玻爾茲曼機的可見元和隱元之間是全連線的，而且隱元和隱元之間也是全連線的，這樣就增加了計算量和計算難度。
“受限玻爾茲曼機”（RBM）同樣具有一個可見層，一個隱層，但層內無連線，層與層之間全連線，節點變數仍然取值為0或1，是一個二分圖。也就是將“玻爾茲曼機”（BM）的層內連線去掉，對連線進行限制，就變成了“受限玻爾茲曼機”（RBM），這樣就使得計算量大大減小，使用起來也就方便了很多。如上圖。
“受限玻爾茲曼機”（RBM）的特點是：在給定可見層單元狀態（輸入資料）時，各隱層單元的啟用條件是獨立的（層內無連線），同樣，在給定隱層單元狀態時，可見層單元的啟用條件也是獨立的。

跟“玻爾茲曼機”（BM）類似，根據玻爾茲曼分佈，可見層（變數為v，偏置量為a）、隱層（變數為h，偏置量為b）的概率為：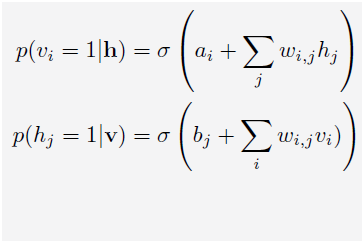
 
訓練樣本的對數似然函式為：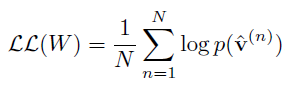
 
求導數：
 
總之，還是挺複雜的，計算也還是挺花時間的。
同樣，可以通過Gibbs 取樣的方法來近似計算。雖然比一般的玻爾茲曼機速度有很大提高，但一般還是需要通過很多步取樣才可以採集到符合真實分佈的樣本。這就使得受限玻爾茲曼機的訓練效率仍然不高。
2002年，大神Hinton再出手，提出了“對比散度”（Contrastive Divergence，簡稱CD）演算法，這是一種比Gibbs取樣更加有效的學習演算法，促使大家對RBM的關注和研究。

RBM的本質是非監督學習的利器，可以用於降維（隱層設定少一點）、學習提取特徵（隱層輸出就是特徵）、自編碼器（AutoEncoder）以及深度信念網路（多個RBM堆疊而成）等等。

三、深度信念網路（Deep Belief Network，簡稱DBN）
 
2006年，Hinton大神又又又出手了，提出了“深度信念網路”（DBN），並給出了該模型一個高效的學習演算法，這也成了深度學習演算法的主要框架，在該演算法中，一個DBN模型由若干個RBM堆疊而成，訓練過程由低到高逐層進行訓練，如下圖所示：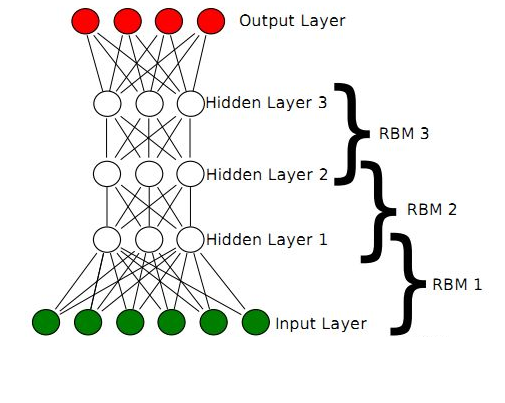
 
回想一下RBM，由可見層、隱層組成，顯元用於接受輸入，隱元用於提取特徵，因此隱元也有個別名，叫特徵檢測器。也就是說，通過RBM訓練之後，可以得到輸入資料的特徵。（感性對比：聯想一下主成分分析，提取特徵）
另外，RBM還通過學習將資料表示成概率模型，一旦模型通過無監督學習被訓練或收斂到一個穩定的狀態，它還可以被用於生成新資料。（感性對比：聯想一下曲線擬合，得出函式，可用於生成資料）

正是由於RBM的以上特點，使得DBN逐層進行訓練變得有效，通過隱層提取特徵使後面層次的訓練資料更加有代表性，通過可生成新資料能解決樣本量不足的問題。逐層的訓練過程如下：
（1）最底部RBM以原始輸入資料進行訓練
（2）將底部RBM抽取的特徵作為頂部RBM的輸入繼續訓練
（3）重複這個過程訓練以儘可能多的RBM層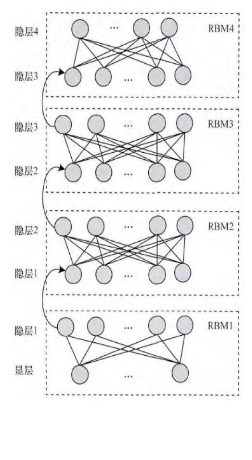
 
由於RBM可通過CD快速訓練，於是這個框架繞過直接從整體上對DBN高度複雜的訓練，而是將DBN的訓練簡化為對多個RBM的訓練，從而簡化問題。而且通過這種方式訓練後，可以再通過傳統的全域性學習演算法（如BP演算法）對網路進行微調，從而使模型收斂到區域性最優點，通過這種方式可高效訓練出一個深層網路出來，如下圖所示：

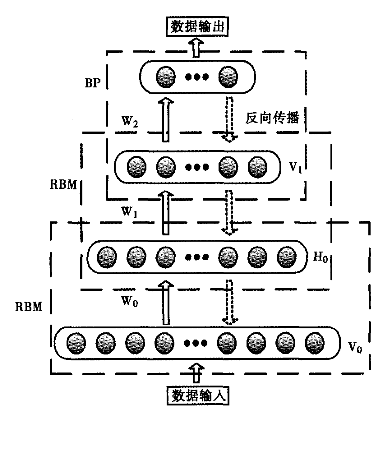
Hinton提出，這種預訓練過程是一種無監督的逐層預訓練的通用技術，也就是說，不是隻有RBM可以堆疊成一個深度網路，其它型別的網路也可以使用相同的方法來生成網路。

牆裂建議

Hinton 大神寫了一篇關於受限玻爾茲曼機的訓練實用指南（《A Practical Guide to Training Restricted Boltzmann Machines》），非常詳細地描述訓練過程，建議仔細閱讀下這篇論文，肯定大有收穫。

掃描以下二維碼關注本人公眾號“大資料與人工智慧Lab”（BigdataAILab），然後回覆“論文”關鍵字可線上閱讀這兩篇經典論文的內容。

推薦相關閱讀