效果圖:

在本教程中我們將學習如何估計人類的姿勢使用OpenCV和Dlib照片。

在進行本教程之前，我想指出這個帖子屬於我在面部處理中編寫的一個系列。下面的一些文章有助於理解這篇文章，而其他文章補充了這一點。

2.臉部變換

3.臉平均化

4.臉部變形

什麼是姿勢估計？

在計算機視覺中，物體的姿態是指相對於相機的相對取向和位置。您可以通過相對於相機移動物件或相機物件來更改姿勢。

本教程中描述的姿態估計問題通常在計算機視覺術語中被稱為透視n點問題或PNP。我們將在下面的章節中更詳細地看到，在這個問題中，我們的目標是在我們有一個校準的相機時找到一個物件的姿態，並且我們知道物件上的n個3D點的位置和相應的2D投影圖片。

如何以數學方式表示相機運動？

3D剛體對照相機只有兩種運動。

（1）平移：將相機從當前的3D位置（X，Y，Z）移動到新的3D位置（X'，Y'，Z'）被稱為平移。你可以看到有3個自由度——你可以在X，Y或Z方向移動。向量t由（X'-X，Y'-Y，Z'-Z）表示。

（2）旋轉：你也可以繞X，Y和Z軸旋轉相機。因此，旋轉也具有三個自由度。有許多表示旋轉的方式，您可以使用：

1）尤拉角（roll滾動，pitch俯仰和yaw偏航）

2）3x3旋轉矩陣

因此，估計3D物件的姿態意味著找到6個數字——3個用於平移，3個用於旋轉。

你需要什麼姿勢估計？

要計算影象中物件的3D姿態，您需要以下資訊：

（1）幾個點的2D座標：你需要在影象中幾個點的2D（X，Y）的位置。在臉部的情況下，您可以選擇眼睛的角落，鼻尖，嘴角等。Dlib的facial landmarkdetector為我們提供了很多選擇。在本教程中，我們將使用鼻尖，下巴，左眼的左角，右眼的右角，嘴的左角和嘴的右角。

       （2）上述相同點的3D位置：您還需要2D特徵點的3D位置。您可能會認為，您需要在照片中的人的3D模型來獲取3D位置。理想中是的，但，實際上並不需要。通用的3D模型就足夠了。從哪裡得到一個頭像的3D模型？好吧，你並非真的需要一個完整的3D模型。您僅僅需要在某些任意參考框架中的幾個點的3D位置。在本教程中，我們將使用以下3D點：

       1）鼻尖：（0.0，0.0，0.0）

       2）下巴：（0.0，-330.0，-65.0）

       3）左眼左角：（-225.0f，170.0f，-135.0）

       4）右眼右角:( 225.0，170.0，-135.0）

       5）嘴角左側：（-150.0，-150.0，-125.0）

6）嘴角右側：（150.0，-150.0，-125.0）

請注意，以上幾點在某些任意的參考幀/座標系中。這被稱為世界座標系(a.k.a OpenCV文件中的模型座標 )。

       （3）相機的內參數。如前所述，在這個問題中，假設相機被校準。換句話說，您需要知道相機的焦距，影象中的光學中心和徑向失真引數。所以你需要校準你的相機。當然，對於我們之間的懶惰和愚蠢的人，這太多了。我可以提供捷徑嗎？當然，我可以！通過不使用準確的3D模型我們已經可以近似的去確定。我們可以通過影象的中心逼近光學中心，將焦距近似為畫素的寬度，並假設不存在徑向失真。Boom! you did not even have to get up from your couch!

姿態估計演算法如何工作？

有幾種姿態估計演算法。第一個已知的演算法可以追溯到1841年。來解釋這些演算法的細節已經超過這篇文章的範圍，但它是一個一般的想法。

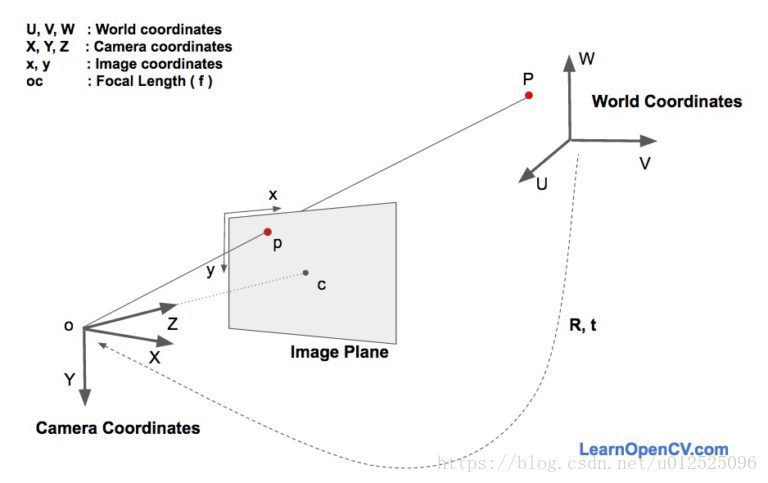
這裡有三個座標系。各種面部特徵的3D座標是建立在世界座標系中。如果我們知道旋轉和平移（即姿勢），我們可以將世界座標中的3D點變換為相機座標中的3D點。可以使用相機的固有引數（焦距，光學中心等）將相機座標中的3D點投影到影象平面（即影象座標系）上。

我們來看看影象形成的方程，以瞭解上述座標系的工作原理。在上圖中，o是相機的中心，圖中所示的平面是影象平面。我們有興趣找出“什麼樣的方程可以將3D點p的投影P對映在影象平面上”。

假設我們知道世界座標中3D點P的位置（U，V，W）。假設我們知道旋轉矩陣R（3x3矩陣）和平移t（3x1向量），他們都建立在相對於相機座標系的世界座標系中，我們可以使用以下公式計算攝像機座標系中點P的位置（X，Y，Z）。

公式（1）

以擴充套件形式，上述方程如下所示：

公式（2）

如果你已經學習了線性代數，你會認識到，如果我們知道足夠數量的點對應（即（X，Y，Z）和（U，V，W）），上面是一個線性方程組。 和 是未知數，您可以輕鬆地解出未知數。

正如你將在下一節中看到的，我們知道（X，Y，Z）只是一個未知的規模（階），所以我們沒有一個簡單的線性系統。

直接線性變換

我們知道3D模型上的許多點（即（U，V，W）），但是我們不知道（X，Y，Z）。 我們只知道2D點的位置（即（x，y））。 在沒有徑向變形的情況下，影象座標中點p的座標（x，y）由下式給出：

公式（3）

其中， 和 是x和y方向上的焦距， 是光學中心。當涉及徑向扭曲時，事情變得複雜得多，為了簡單起見，我將其拋棄。

在方程式中的S呢？這是一個未知的比例因子。它存在於等式中，因為在任何影象中我們不知道影象的深度。如果將3D中的任何點P連線到相機的中心o，則光線與影象平面相交的點p是P的影象。注意，沿著連線相機中心的點的所有點和點P產生相同的影象。換句話說，使用上述等式，您只能獲得（X，Y，Z）達到刻度s。

現在這干擾了方程式2，因為它不再是我們知道如何解決的好的線性方程。我們的方程看起來更像：

公式（4）

幸運的是，使用一種稱為直接線性變換（DirectLinear Transform，DLT）的方法，可以使用一些代數魔法解決上述形式的方程。只要您發現方程幾乎是線性但是有一個未知比例的問題，您可以使用DLT。

Levenberg-Marquardt優化

上述DLT解決方案不是很準確，原因如下。首先，旋轉R具有三個自由度，但在DLT解決方案中使用的矩陣表示具有9個數字。DLT解決方案中沒有任何內容迫使估計的3×3矩陣成為旋轉矩陣。更重要的是，DLT解決方案不會使正確的目標函式最小化。理想情況下，我們希望最大限度地減少以下描述的重新投射錯誤(reprojection error)。

如等式2和3所示，如果我們知道正確的姿勢（R和t），我們可以通過將3D點投影到影象上來預測影象上3D面部點的2D位置。換句話說，如果我們知道R和t，我們可以在每個3D點P的影象中找到點p。

我們也知道2D面部特徵點（使用Dlib或手動點選）。我們可以看看投影3D點和2D面部特徵之間的距離。當估計的姿勢是完美的，投影到影象平面上的3D點將幾乎完美地與2D面部特徵相匹配。當姿態估計不正確時，我們可以計算重投影誤差量度——投影3D點與2D面部特徵點之間的平方距離之和。

如前所述，可以使用DLT解決方案找到姿態的近似估計（R和t）。改善DLT解決方案的一個天真的方法是輕輕隨意地改變姿勢（R和t），並檢查重新投射錯誤是否減少。如果是這樣，我們可以接受新的姿勢估計。我們可以一次又一次地保持擾亂R和t來找到更好的估計。雖然這個程式會奏效，但是會很慢。原來，有原則的方法迭代地改變R和t的值，以使重新投射錯誤減少。一種這樣的方法稱為Levenberg-Marquardt優化。檢視維基百科上的更多細節。

OpenCV solvePnP

在OpenCV中，函式solvePnP和solvePnPRansac可用於估計姿態。

solvePnP實現了幾種用於姿態估計的演算法，可以使用引數標誌來選擇。預設情況下，它使用標誌SOLVEPNP_ITERATIVE，它本質上是DLT解決方案通過Levenberg-Marquardt優化。SOLVEPNP_P3P僅使用3點來計算姿勢，只有在使用solvePnPRansac時才使用它。

在OpenCV 3中，引入了兩種新的方法——SOLVEPNP_DLS和SOLVEPNP_UPNP。關於SOLVEPNP_UPNP的有趣之處在於它也試圖估計攝像機的內部引數。

C++: bool solvePnP(InputArrayobjectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArraydistCoeffs, OutputArray rvec, OutputArray tvec, bool useExtrinsicGuess=false,int flags=SOLVEPNP_ITERATIVE )

Parameters:

       objectPoints - 世界座標空間中的物件點陣列。我通常通過N個3D點的向量。您還可以傳遞大小為Nx3（或3xN）單通道矩陣，或Nx1（或1xN）3通道矩陣的Mat。我強烈推薦使用向量。

imagePoints - 對應影象點的陣列。你應該傳遞一個N 2D點的向量。但您也可以通過2xN（或Nx2）1通道或1xN（或Nx1）2通道墊，其中N是點數。

cameraMatrix - 輸入相機矩陣A = 。注意，在某些情況下， ， 可以通過畫素的影象寬度來近似，並且 和 可以是影象中心的座標。

distCoeffs - 4，5，8或12個元素的失真係數（ ， ， ， [ [ ， ， ]，[ ， ， ， ]]的輸入向量。如果向量為空/空，則假定零失真係數。除非您正在使用像變形巨大的Go-Pro像相機，否則我們可以將其設定為NULL。如果您正在使用高失真鏡頭，建議您進行全面的相機校準。

rvec - 輸出旋轉向量。

tvec - 輸出平移向量。

useExtrinsicGuess - 用於SOLVEPNP_ITERATIVE的引數。如果為真（1），則函式使用提供的rvec和tvec值作為旋轉和平移向量的初始近似值，並進一步優化它們。

Method for solving a PnP problem：

SOLVEPNP_ITERATIVE迭代法基於Levenberg-Marquardt優化。在這種情況下，該功能可以找到這樣一種姿態，使重播誤差最小化，即觀察到的投影影象點與投影（使用projectPoints（））物件點之間的距離之間的平方和之和。

SOLVEPNP_P3P方法是基於X.S.的論文。高，X.-R。 Hou，J. Tang，H.-F. Chang“三點問題的完整解決方案分類”。在這種情況下，該功能只需要四個物件和影象點。

SOLVEPNP_EPNP方法由F.Moreno-Noguer，V.Lepetit和P.Fua在論文“EPnP：Efficient Perspective-n-Point Camera Pose Estimation”中引入。

以下標誌僅適用於OpenCV 3

SOLVEPNP_DLS方法基於Joel A. Hesch和Stergios I. Roumeliotis的論文。 “PnP的直接最小二乘法（DLS）方法”。

SOLVEPNP_UPNP方法基於A.Penate-Sanchez，J.Andrade-Cetto，M.Moreno-Noguer的論文。 “用於強大的相機姿態和焦距估計的窮盡線性化”。在這種情況下，假設兩者都具有相同的值，函式也估計引數f_x和f_y。然後用估計的焦距更新cameraMatrix。

OpenCV solvePnPRansac

solvePnPRansac與solvePnP非常相似，只是它使用隨機樣本一致性（RANSAC）來魯棒估計姿勢。

當您懷疑幾個資料點非常嘈雜時，使用RANSAC非常有用。例如，考慮將線擬合到2D點的問題。使用線性最小二乘法可以解決這個問題，其中從擬合線的所有點的距離最小化。現在考慮一個非常糟糕的資料點。這一個資料點可以控制最小二乘解決方案，我們對該行的估計將是非常錯誤的。在RANSAC中，通過隨機選擇最小點數來估計引數。線上擬合問題中，我們從所有資料中隨機選擇兩個點，並找到通過它們的線。距離線路足夠近的其他資料點稱為內聯。通過隨機選擇兩個點來獲得線的幾個估計，並且選擇具有最大數目的線內值的線作為正確估計。

solvePnPRansac的使用如下所示，並解釋了對於solpnPRansac特定的引數。

C++:void solvePnPRansac(InputArrayobjectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArraydistCoeffs, OutputArray rvec, OutputArray tvec, bool useExtrinsicGuess=false,int iterationsCount=100, float reprojectionError=8.0, int minInliersCount=100,OutputArray inliers=noArray(), int flags=ITERATIVE )

iterationsCount - 選擇最小點數和估計引數的次數。

reprojectionError - 如前所述，在RANSAC中，預測足夠近的點被稱為“內在”。該引數值是觀測值和計算點投影之間的最大允許距離，以將其視為一個惰性。

minInliersCount - 內聯數。如果在某個階段的演算法比minInliersCount發現更多的核心，它會完成。

inliers - 包含objectPoints和imagePoints中的內聯索引的輸出向量。

OpenCV POSIT

OpenCV用於稱為POSIT的姿態估計演算法。 它仍然存在於C的API（cvPosit）中，但不是C ++API的一部分。 POSIT假設一個縮放的正交相機模型，因此您不需要提供焦距估計。此功能現在已經過時了，我建議您使用solvePnp中實現的一種演算法。

OpenCV姿勢估計程式碼：C ++ / Python

在本節中，我在C ++和Python中共享了一個示例程式碼，用於單個影象中的頭部姿態估計。您可以在這裡下載圖片headPose.jpg。

面部特徵點的位置是硬編碼（設定好的）的，如果要使用自己的影象，則需要更改向量image_points（特徵點，上面說的下巴、眼睛、鼻尖等）。

#include <opencv2/opencv.hpp>

using namespace std;

using namespace cv;

int main(int argc, char **argv)

{

// Read inputimage

cv::Mat im =cv::imread("headPose.jpg");

// 2D imagepoints. If you change the image, you need to change vector

std::vector<cv::Point2d>image_points;

image_points.push_back(cv::Point2d(359, 391) );    // Nose tip

image_points.push_back(cv::Point2d(399, 561) );    // Chin

image_points.push_back(cv::Point2d(337, 297) );     // Left eye left corner

image_points.push_back(cv::Point2d(513, 301) );    // Right eye right corner

image_points.push_back(cv::Point2d(345, 465) );    // Left Mouth corner

image_points.push_back(cv::Point2d(453, 469) );    // Right mouth corner

// 3D modelpoints.

std::vector<cv::Point3d>model_points;

model_points.push_back(cv::Point3d(0.0f,0.0f,0.0f));              // Nose tip

model_points.push_back(cv::Point3d(0.0f,-330.0f, -65.0f));          //Chin

model_points.push_back(cv::Point3d(-225.0f,170.0f, -135.0f));       // Left eye left corner

model_points.push_back(cv::Point3d(225.0f,170.0f, -135.0f));        // Right eye rightcorner

model_points.push_back(cv::Point3d(-150.0f,-150.0f, -125.0f));      // Left Mouth corner

model_points.push_back(cv::Point3d(150.0f,-150.0f, -125.0f));       // Right mouth corner

// Camerainternals

doublefocal_length = im.cols; // Approximate focal length.

Point2d center =cv::Point2d(im.cols/2,im.rows/2);

cv::Matcamera_matrix = (cv::Mat_<double>(3,3) << focal_length, 0,center.x, 0 , focal_length, center.y, 0, 0, 1);

cv::Matdist_coeffs = cv::Mat::zeros(4,1,cv::DataType<double>::type); // Assumingno lens distortion

cout <<"Camera Matrix " << endl << camera_matrix << endl ;

// Outputrotation and translation

cv::Matrotation_vector; // Rotation in axis-angle form

cv::Mattranslation_vector;

// Solve forpose

cv::solvePnP(model_points,image_points, camera_matrix, dist_coeffs, rotation_vector, translation_vector);

// Project a 3Dpoint (0, 0, 1000.0) onto the image plane.

// We use thisto draw a line sticking out of the nose

vector<Point3d>nose_end_point3D;

vector<Point2d>nose_end_point2D;

nose_end_point3D.push_back(Point3d(0,0,1000.0));

projectPoints(nose_end_point3D,rotation_vector, translation_vector, camera_matrix, dist_coeffs,nose_end_point2D);

for(int i=0; i< image_points.size(); i++)

{

circle(im,image_points[i], 3, Scalar(0,0,255), -1);

}

cv::line(im,image_points[0],nose_end_point2D[0], cv::Scalar(255,0,0), 2);

cout <<"Rotation Vector " << endl << rotation_vector <<endl;

cout <<"Translation Vector" << endl << translation_vector<< endl;

cout<<  nose_end_point2D << endl;

// Displayimage.

cv::imshow("Output",im);

cv::waitKey(0);

}

使用Dlib實時姿態估計

這篇文章中包含的視訊是使用我的dlib分支，可以免費為這個部落格的訂閱者使用。如果您已經訂閱，請檢視歡迎電子郵件連結到我的dlib fork，並檢視此檔案。

dlib/examples/webcam_head_pose.cpp

Dlib中獲取的各個點

std::vectorget_2d_image_points(full_object_detection &d)
{
std::vector image_points;
image_points.push_back( cv::Point2d(d.part(30).x(), d.part(30).y() ) ); // Nose tip
image_points.push_back( cv::Point2d(d.part(8).x(), d.part(8).y() ) ); // Chin
image_points.push_back( cv::Point2d(d.part(36).x(), d.part(36).y() ) ); // Left eye left corner
image_points.push_back( cv::Point2d(d.part(45).x(), d.part(45).y() ) ); // Right eye right corner
image_points.push_back( cv::Point2d(d.part(48).x(), d.part(48).y() ) ); // Left Mouth corner
image_points.push_back( cv::Point2d(d.part(54).x(), d.part(54).y() ) ); // Right mouth corner
return image_points;

}