題面

傳送門

分析

假設k是固定的，那訪問到的節點編號就是\(1+(a·k \mod n )\)，其中a為正整數。

通過找規律不難發現會出現迴圈。

通過題目中的圖片我們不難發現

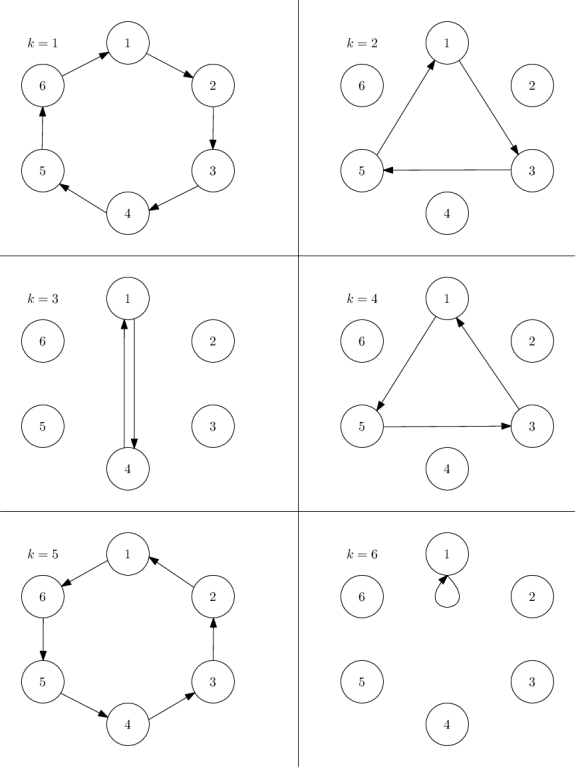
只有k=1,2,3,6得到的四種結果，而其他的情況都和這4種結果的某種一樣

所以我們只要考慮n的因數即可

對於固定的k我們發現訪問到的節點為1,1+k,1+2k.....n-k+1,一共\(\frac{n}{k}\) 項，根據等差數列求和公式和為\(\frac{n(n-k+2)}{2k}\)

所以我們只要在\(O(\sqrt n)\)的時間內分解因數，然後再\(O(1)\)更新答案即可

程式碼

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#define maxn 100005
using namespace std;
long long n,k;
long long a[maxn];
int cnt=0;
vector<long long>ans;
void div(long long n){
    for(long long i=2;i*i<=n;i++){
        if(n%i==0){
            a[++cnt]=i;
            if(i!=n/i) a[++cnt]=n/i; 
        }
    }
}
int main(){
    scanf("%I64d",&n);
    div(n);
    for(int i=1;i<=cnt;i++){
        long long x=a[i];
        long long f=n/x*(n-x+2)/2;
        ans.push_back(f); 
    }
    sort(ans.begin(),ans.end());
    for(int i=0;i<ans.size();i++){
        printf("%I64d ",ans[i]);
    }
}