滑動視窗法詳解
阿新 • • 發佈:2019-01-08
演算法目的
該演算法展示瞭如何將巢狀for迴圈在少數問題中轉換為單個for迴圈,從而減少了時間的複雜性。
前言
一個經典的問題
給一組大小為n的整數陣列,計算長度為k的子陣列的最大值
我們希望的結果如下
Input : arr[] = {100, 200, 300, 400}
k = 2
Output : 700
Input : arr[] = {1, 4, 2, 10, 23, 3, 1, 0, 20}
k = 4
Output : 39
We get maximum sum by adding subarray {4 該技術可以通過總線上的窗格得到最好的理解,考慮長度為n的視窗和長度為k的窗格。考慮一下,最初窗格處於極端的左邊,即從左邊開始的0個單位。現在,將視窗與大小為n和平面的陣列arr []以k大小的元素的current_sum相關聯。現在,如果我們在窗戶上施加力量,使其向前移動一個單位距離。該窗格將覆蓋下一個k個連續元素。
考慮陣列arr [] = { 5,2,-1,0,3 },k = 3和n = 5的值
應用滑動視窗技術:
- 我們使用線性迴圈計算n個項中前k個元素的總和,並將總和儲存在變數window_sum中。
- 然後,我們將在陣列上線性滑動直至達到最終並同時追蹤最大和。
- 要獲得k個元素塊的當前總和,只需從前一個塊中減去第一個元素並添加當前塊的最後一個元素即可。 下面的表示將清楚說明視窗如何在陣列上滑動。
這是我們計算從索引0開始的初始視窗總和的初始階段。在這個階段,視窗和為6.現在,我們將maximum_sum設定為current_window,即6。

現在,我們用單位索引來滑動我們的視窗。因此,現在它從視窗中丟棄5並將0新增到視窗。因此,我們將得到新的視窗總和,減去5,然後加上0。所以,我們的視窗和現在變成1.現在,我們將比較這個視窗和與maximum_sum。因為它更小,我們不會改變maximum_sum。
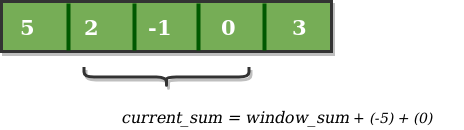
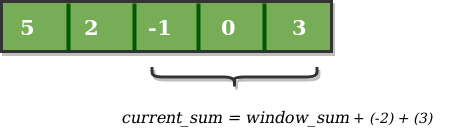
同樣,現在我們再次用一個單位索引來滑動我們的視窗,並獲得新的視窗總和為2.我們再一次檢查這個當前視窗總和是否大於maximum_sum,直到現在。有一次,它再小一些,所以我們不改變maximum_sum。
因此,對於上面的陣列,我們的maximum_sum是6。
程式碼如下
#include <iostream>
using namespace std;
int maxSum(int arr[], int n, int k)
{
if (n < k)
{
cout << "Invaild";
return -1;
}
int max_sum = 0;
for (int i=0; i<k; i++)
{
max_sum += arr[i];
}
int windows_sum = max_sum;
for (int i=k; i<n; i++)
{
windows_sum += arr[i] - arr[i - k];
max_sum = max(max_sum, windows_sum);
}
return max_sum;
}
int main()
{
int arr[] = {1, 4, 2, 10, 2, 3, 1, 0, 20};
int k = 4;
int n = sizeof(arr) / sizeof(arr[0]);
cout << maxSum(arr, n, k);
return 0;
}總結
現在,很明顯時間複雜性是線性的,因為我們可以看到只有一個迴圈執行在我們的程式碼中。因此,我們的時間複雜度是O(n)。
我們可以使用這種技術來查詢最大/最小k-子陣列,XOR,乘積,總和等
