RNN, LSTM, GRU 公式總結
Vanilla RNN
參考 RNN wiki 的描述,根據隱層

- Elman network 接受上時刻的隱層
ht−1 - Jordan network 接受上時刻的輸出
yt−1
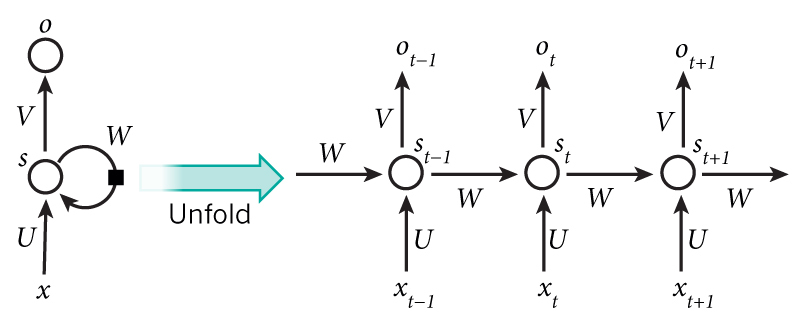
Bidirectional RNNs
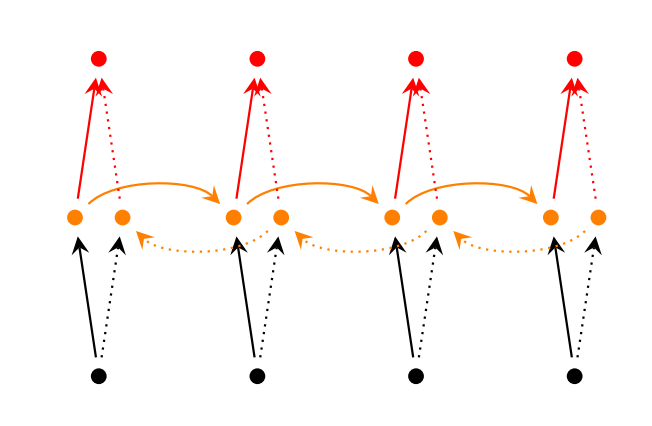
雙向的 RNN 是同時考慮“過去”和“未來”的資訊,考慮上圖,正常情況下,輸入(黑色點)沿著黑色的實線箭頭傳輸到隱層(黃色點),再沿著紅色實線傳到輸出(紅色點)。黑色實線做完前向傳播後,在 Bidirectional RNNs 卻先不急著後向傳播,而是從末尾的時刻沿著虛線的方向再回傳回來。最後把兩個方向得到的啟用值拼在一起(concatenate),當做最後的啟用值。那麼後向傳播也是類似,要轉一圈回來。
Stacked Bidirectional RNNs
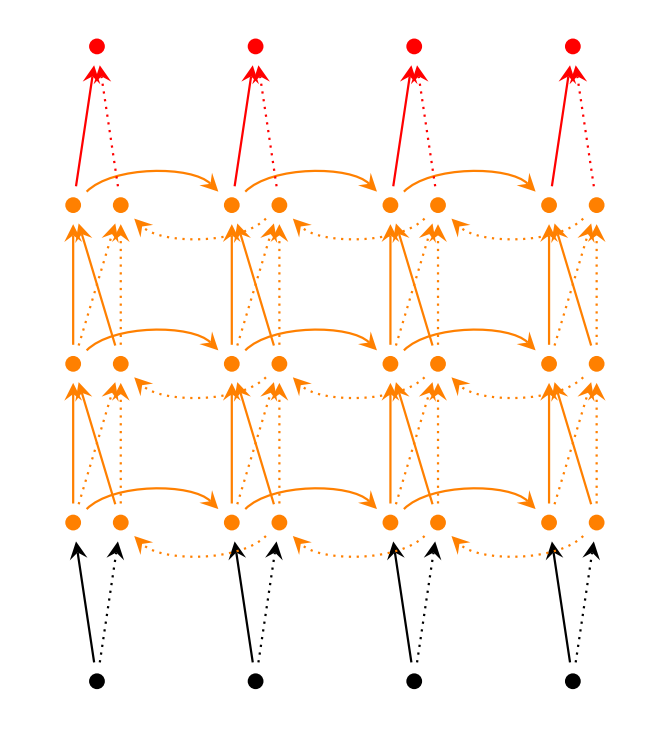
堆多層的 recurrent layer,如上圖所示,可以增加模型的引數,提高模型的學習能力。每層的 hidden state 不僅要輸給下一時刻,還是當做是此時刻下一層的輸入。上圖展示了雙向的三層 RNNs,那麼 hidden state 的維度是 hidden_dim * 6,輸出的維度為 hidden_dim * 2,因為是兩個方向最有一層 hidden state 拼接的結果。
原始的 RNN 很難訓練,主要是因為存在梯度消失(gradient vanishing problem)和梯度爆炸問題(gradient explosion problem)。梯度消失導致無法抓住長時刻依賴,因此效果不好,後面的 LSTM 和 GRU 的新結構,就是為了對付這個問題。而梯度爆炸問題雖然不是每次都出現,但是一旦出現就很致命。一般會選擇用截斷的梯度(clipped gradient)來更新引數,或者直接把梯度 rescale 到一個固定模大小的範圍。
LSTM
由於 Vanilla RNN 具有梯度消失問題,對長關係的依賴(Long-Term Dependencies)的建模能力不夠強大。這句話是什麼意思呢?就是說,原來的 RNN,由於結構上的限制,很長的時刻以前的輸入,對現在的網路影響非常小,後向傳播時那些梯度,也很難影響很早以前的輸入,即會出現梯度消失的問題。而 LSTM 通過構建一些門(Gate),讓網路能記住那些非常重要的資訊,而這個核心的結構,就是 cell state。比如遺忘門,來選擇性清空過去的記憶和更新較新的資訊。
上面講的比較迷糊,如果我有新的理解會更新這個部落格。另外可以參考大神的部落格 Understanding LSTM Networks
有兩種常見的 LSTM 結構,如 LSTM wiki 總結的,第一種是帶遺忘門的 Traditional LSTM,公式如下:

前三行是三個門,分別是遺忘門
注意這裡的輸出
有時候第四個公式裡的
第二種是帶遺忘門的 Peephole LSTM,公式如下,

和上面的公式做比較,發現只是把
還有把兩種結構結合起來的,可以用下圖描述,
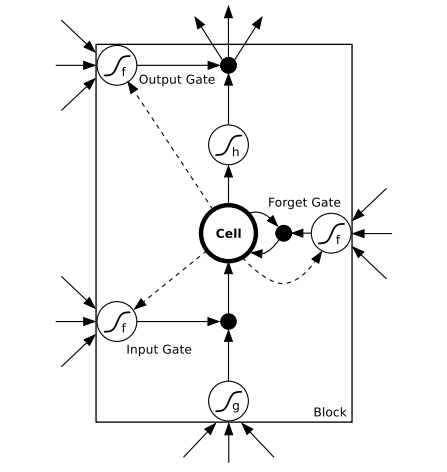
圖裡的連著門的那些虛線就是窺視孔。三個輸入分別是
GRU
GRU 的結構和 LSTM 類似,但是精簡一些,見下圖
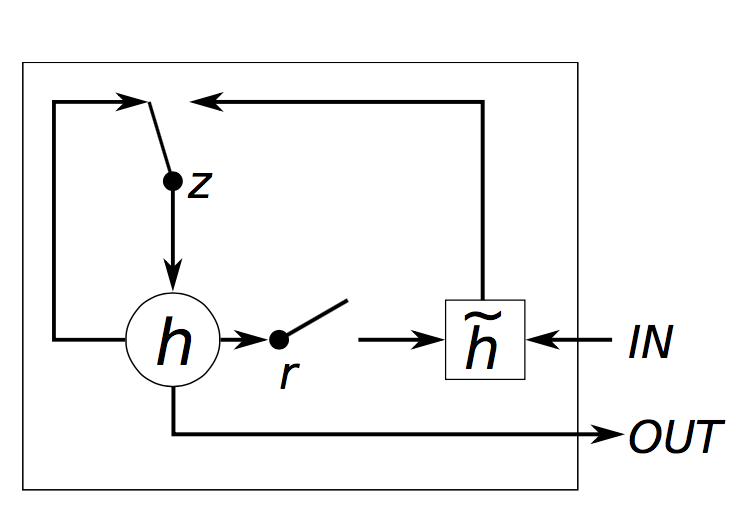
公式如下:
這四行公式解釋如下:
zt 是 update gate,更新 activation 時的邏輯閘rt 是 reset gate,決定 candidate activation 時,
