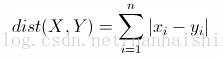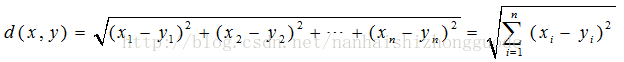第二章 提供推薦 （一）協作型過濾 Collaborative Filtering
如果想了解商品、影片或網站的推薦性資訊，最沒有技術含量的方法是向朋友們詢問，其中一部分人的品味會比其他人高一些，通過觀察這些人是否通常也和我們一樣喜歡同樣的東西，可以逐步對這些情況有所瞭解。不過隨著選擇越來越多，想要通過詢問一小群人來確定我們想要的東西，將會變得越來越不實際。因為他們可能並不瞭解所有的選擇。這就是為什麼人們要發展出一套被稱作協作型過濾（collaborative filteriing）的技術。
一個協作型過濾演算法通常是對一大群人進行搜尋，並從中找到與我們品味相近的一小群人。演算法會對這些人所偏愛的其他內容進行考察，並從中找出與我們品味相近的一小群人。演算法會對這些人所偏愛的其他內容進行考察，並將他們組合起來構造出一個經過排名的推薦列表。有不同的方法可以幫助我們確定那些人與自己品味相近，並將他們的選擇組合成列表。


（二）蒐集偏好 Collecting Perferences
我們要做的第一件事情，是尋找一種表達不同人及其偏好的方法。在python中，達到這一目的的一種非常簡單的方法是使用一個巢狀的字典。我們新建一個名為recommendations.py的檔案，並加入如下程式碼來構造一個數據集：
#一個涉及影評者及其對幾部影片評分情況的字典

critics={'Lisa Rose':{'Lady in the Water':2.5,'Snakes on a Plane':3.5,
                      'Just My Luck':3.0,'Superman Returns':3.5,
                      'You,Me and Dupree':2.5,'The Night Listener':3.0},                    
         'Gene Seymour':{'Lady in the Water':3.0,'Snakes on a Plane':3.5, 
                         'Just My Luck':1.5,'Superman Returns':5.0,
                         'The Nighr Listener':3.0,'You,Me and Dupree':3.5},
         'Michael Phillips':{'Lady in the Water':2.5,'Snakes on a Plane':3.0,
                              'Superman Returns':3.5,'The Nighr Listener':4.0},
         'Claudia Puig':{'Snakes on a Plane':3.5,'Just My Luck':3.0,
                         'The Night Listener':4.5,'Superman Returns':4.0,
                         'You,Me and Dupree':2.5},
         'Mick LaSalle':{'Lady in the Water':3.0,'Snakes on a Plane':4.0,
                         'Just My Luck':2.0,'Superman Returns':3.0,
                         'The Night Listener':3.0,'You,Me and Dupree':2.0},
         'Jack Matthews':{'Lady in the Water':3.0,'Snakes on a Plane':4.0,
                          'The Night Listener':3.0,'Superman Returns':5.0,
                          'You,Me and Dupree':3.5},
         'Toby':{'Snakes on a Plane':4.5,'You,Me and Dupree':1.0,
                 'Superman Returns':4.0}}
                         
 

本章中，我們將以互動式方式使用python，因此，應該先將recommendations.py儲存起來，以便python的互動解釋程式能夠讀取到它。我們也可以將檔案儲存在 python/Lib 目錄下，
不過最為簡單的作法，是在與我們儲存檔案的同一目錄下啟動python解釋程式。

上述字典使用從1到5的評分，以此來體現包括本人在內的每位影評人對某一給定影片的喜愛程度。不管偏好是如何表達的，我們需要一種方法來將它們對應到數字。加入我們正在架構一個購物網站，不妨用數字1來表示有人過去曾購買過某件商品，用數字0表示未曾購買過任何商品。而對於一個新聞故事的投票網站，我們可以分別用數字-1，0和1來表達“不喜歡”，“沒有投票”，“喜歡”，如表2-1所示：

表2-1：從使用者行為到相應評價值的可能對應關係

音樂會門票	線上購物	網站推薦者
已購買	1	已購買	2	喜歡	1
未購買	0	已瀏覽	1	未投票	0
未購買	0	不喜歡	-1

對於演算法實驗和範例演示而言，使用字典也是很方便的。我們可以很容易地對字典進行查詢和修改。啟用Python，並輸入以下幾行命令：

from recommendations import critics
#從檔案recommendations.py中匯入字典critics
critics['Lisa Rose']['Lady in the Water']
#查詢Lisa Rose對影片“Lady in the Water”的評分
critics['Toby']['Snakes on a Plane']=4.5
#增加Toby對影片“Snakes on a Plane”的評分
critics['Toby']
#查詢Toby的所有資訊

儘管可以將相當數量的人員偏好資訊置於字典內（即記憶體中），但對於一個規模巨大的資料及而言，也許我們還是會希望將其存入資料庫中。

（三）尋找相近的使用者 Finding Similar Users

蒐集完人們的偏好資料後，我們需要有一種方法來確定人們在品位方面的相似程度。為此，我們可以將每個人與所有其他人進行對比，並計算他們的相似度評價值。有若干種方法可以達到此目的，下面是兩套計算相似度評價值的體系：歐幾里得距離和皮爾遜相關度。

歐幾里得度量定義歐幾里得空間中點 x = (x1,...,xn) 和 y = (y1,...,yn) 之間的距離為

歐幾里得距離評價：
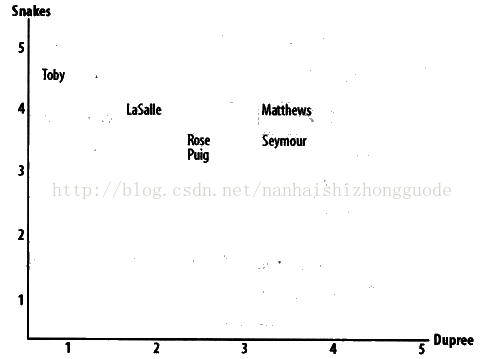
計算相似度評價值的一個非常簡單的方法是使用歐幾里得距離評價方法。它以經過人們一致評價的物品作為座標軸，然後將參與評價的人繪製到圖上，並考察他們彼此之間的距離遠近，如圖2-1所示：

圖2-1： 處於“偏好空間”中的人們

該圖顯示了處於“偏好空間”中人們的分佈情況。Toby在Snake軸線和Dupree周線上所標示的數值分別是4.5和1.0，兩人在“偏好空間”中的距離越近，他們的興趣偏好就越相似。因為這張圖是二維的，所以在同一時間內只能看到兩項評分，但這一規則對於更多數量的評分項而言也是實用的。

為了計算圖上Toby和LaSalle之間的距離，我們可以計算出每一軸向上的差值，求平方後再相加，最後對總和取平方根。在Python中，我們可以用函式pow（n，2）對某數求平方，並使用sqrt函式求平方根：

from math import sqrtsqrt(pow(4.5-4,2)+pow(1-2,2)) 1.118033988749895
“(注: 1. pow() 方法返回 xy（x的y次方） 的值。以下是math模組pow（）方法的語法：

import math
math.pow(x,y)

內建的pow（）方法：pow（x,y[,z]) 函式是計算x的y次方，如果z在存在，則再對結果進行取模，其結果等效於pow(x,y) %z
注意：pow() 通過內建的方法直接呼叫，內建方法會把引數作為整型，而 math 模組則會把引數轉換為 float。 引數：x -- 數值表示式； y -- 數值表示式； z -- 數值表示式 返回 xy（x的y次方） 的值。 pow(x,2) 等價於 x**y
 2. sqrt()方法返回 x (x>0) 的平方根；  math 模組中 sqrt 函式只能進行浮點數的運算

負數的平方根是虛數（以及複數，即實數和虛數之和），這個需要一個專門的函式 cmath (complex math，複數)的模組做處理：

 import cmath
 cmath.sqrt(-1)

結果為1j

）

上述算式可以計算出距離值，偏好越相似的人，其距離就越短。我們還需要一個函式來對偏好越相近的情況給出越大的值。為此，我們可以將函式值加1（這樣就可以避免遇到被零整除的錯誤了），並取其倒數：

1/(1+sqrt(pow(4.5-4,2)+pow(1-2,2)))

結果：0.4721359549995794

這一新的函式總是返回介於0和1之間的值，返回1表示兩人具有一樣的偏好。我們將前述知識結合起來，就可以構造出用來計算相似度的函式。

將下列程式碼加入recommendations.py

from math import sqrt

#返回一個有關Person1和Person2的基於距離的相似度評價
def sim_distance(prefs,person1,person2):
    #prefs是不同人的偏好的字典，person1和person2分別為字典prefs的兩個關鍵值
    #得到shared_items的列表
    si={} #建立一個字典si，其中關鍵值為item，在此例中即為各個被評價的影片   
    for item in prefs[person1]:
        if item in prefs[person2]:
            si[item]=1

    #如果兩者沒有共同之處，返回0
    if len(si)==0:
        return 0

    #計算所有差值的平方和
    sum_of_squares=sum([pow(prefs[person1][item]-prefs[person2][item],2) for
                         item in prefs[person1] if item in prefs[person2]])
    return 1/(1+sqrt(sum_of_squares))

我們呼叫該函式，分別傳入兩個人的名字，並計算出相似度的評價值。

from imp import reload
reload(recommendations)
recommendations.sim_distance(recommendations.critics,'Lisa Rose','Gene Seymour')

結果：0.29429805508554946

(注：reload（）：

在python中，每一個以 .py結尾的Python檔案都是一個模組。其他的檔案可以通過匯入一個模組來讀取該模組的內容。匯入從本質上來講，就是載入另一個檔案，並能夠讀取那個檔案的內容。一個模組的內容通過這樣的屬效能夠被外部世界使用。

　　這種基於模組的方式使模組變成了Python程式架構的一個核心概念。更大的程式往往以多個模組檔案的形式出現，並且匯入了其他模組檔案的工具。其中的一個模組檔案被設計成主檔案，或叫做頂層檔案（就是那個啟動後能夠執行整個程式的檔案）。

　　預設情況下，模組在第一次被匯入之後，其他的匯入都不再有效。如果此時在另一個視窗中改變並儲存了模組的原始碼檔案，也無法更新該模組。這樣設計的原因在於，匯入是一個開銷很大的操作（匯入必須找到檔案，將其編譯成位元組碼，並且執行程式碼），以至於每個檔案、每個程式執行不能夠重複多於一次。

Python2 中可以直接使用reload(module)過載模組。

Pyhton3中需要使用如下兩種方式：
方式（1）

from imp
imp.reload(module)

方式（2）

from imp import reload
reload(module)

使用reload()時出現如下錯誤
>>> from imp import reload
>>> reload(recommendations)
Traceback (most recent call last):
  File "<pyshell#86>", line 1, in <module>
    reload(recommendations)
NameError: name 'recommendations' is not defined 原因是因為在reload某個模組的時候，需要先import來載入需要的模組，這時候再去reload就不會有問題，具體看下面程式碼:
>>> from imp import reload
>>> import recommendations
>>> reload(recommendations)) （四）皮爾遜相關度評價 Pearson Correlation Score 除了歐幾里得距離，還有一種更復雜的方法來判斷人們興趣的相似度，那就是皮爾遜相關係數。 兩個變數之間的相關係數越高，從一個變數去預測另一個變數的精確度就越高，這是因為相關係數越高，就意味著這兩個變數的共變部分越多，所以從其中一個變數的變化就可越多地獲知另一個變數的變化。如果兩個變數之間的相關係數為1或-1，那麼你完全可由變數X去獲知變數Y的值。
·         當相關係數為0時，X和Y兩變數無關係。
·         當X的值增大，Y也增大，正相關關係，相關係數在0.00與1.00之間
·         當X的值減小，Y也減小，正相關關係，相關係數在0.00與1.00之間
·         當X的值增大，Y減小，負相關關係，相關係數在-1.00與0.00之間
          當X的值減小，Y增大，負相關關係，相關係數在-1.00與0.00之間
相關係數的絕對值越大，相關性越強，相關係數越接近於1和-1，相關度越強，相關係數越接近於0，相關度越弱。
假設有兩個變數X、Y，那麼兩變數間的皮爾遜相關係數可通過以下公式計算：

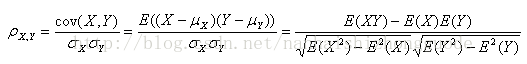
該相關係數是判斷兩組資料與某一直線擬合程度的一種度量。對應的公式比歐幾里得距離評價的計算公式要複雜，但它在資料不是很規範（normalized）的時候（ 比如，影評者對影片的評價總是相對於平均水平偏離很大時），會傾向於給出更好的結果。為了形象地展現這一方法，我們可以在圖上標示出兩位評論者的評分情況，如下圖2-2所示，Mick LaSalle 為《Superman》評了3分，而額Gene Seymour則評了5分，所以該影片被定位在圖中的（3,5）處。

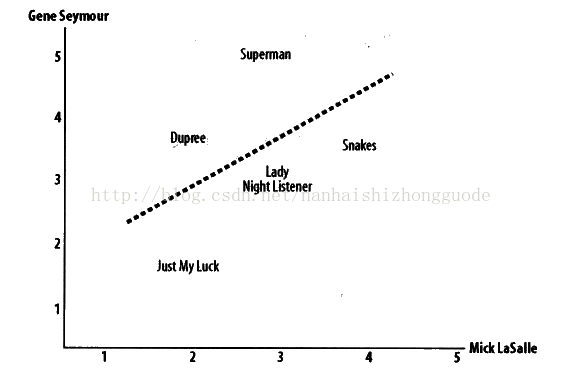
圖2-2： 在散點圖上比較兩位影評者的評分結果 在圖上，我們還可以看到一條直線。因為其繪製原則是儘可能靠近圖上的所有座標點，故被稱為最佳擬合線（best_fit line)。如果兩位評論者對所有影片的評論情況都相同，那麼這條直線將成為對角線，並會與圖上所有的座標點都相交，從而得到一個結果為1的理想相關度評價。對於如上圖所示的情況，由於評論者對部分影片的評分不盡相同，因而相關係數大概在0.4左右。圖2-3展現了一個有著更高相關係數的例子，約為0.75：
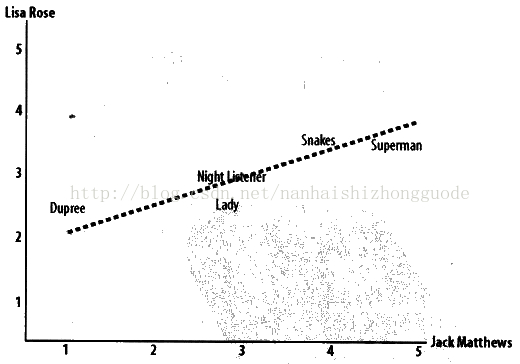
圖2-3： 具有較高相關度評價值的兩位評論者 在採用皮爾遜方法進行評價是，我們可以從圖上發現一個值得注意的地方，那就是它修正了“誇大分值（grade inflation）”的情況。在這張圖中，雖然Jack Matthews總是傾向於給出比Lisa Rose更高的分支，但最終的直線仍然是擬合的，這是因為它們兩者有著相對近似的偏好。如果某人總是傾向於給出比另一個人更好的分值，而兩者的分值之差又始終保持一致，則他們依然可能會存在很好的相關性。此前提到的歐幾里得距離評價方法，會因為一個人的評價始終比另一個人更為“嚴格”（從而導致評價始終相對偏低），而得出兩者不相近的結論，即使他們的品味很相似也是如此。而這一行為是否就是我們想要的結果，則取決於具體的應用場景。 皮爾遜相關度評價演算法首先會找出兩位評論者都曾評價過的物品，然後計算兩者的評分總和與平方和，並求得評分的乘積之和，最後，演算法利用這些計算結果計算出皮爾遜相關係數。不同於距離度量法，這一共是不是分廠只管，但是通過除以將所有變數的變化值相乘後得到的結果，它的確能夠告訴我們變數的總體變化情況。 為了使用這一公式，新建一個與recommendations.py中的sim_distance函式有同樣簽名的函式：

#返回p1和p2的皮爾遜相關係數
def sim_pearson(prefs,p1,p2):
    #得到雙方都曾評價過的物品列表
    si={}
    for item in prefs[p1]:
        if item in prefs[p2]:
            si[item]=1

    #得到列元素的個數
    n=len(si)

    #如果兩者沒有共同之處，返回1
    if n==0：
    return 1

    #對所有偏好求和
    sum1=sum([prefs[p1][it] for it in si])
    sum2=sum([prefs[p2][it] for it in si])

    #求平方和
    sum1sq=sum([pow(prefs[p1][it],2) for it in si])
    sum2sq=sum([pow(prefs[p2][it],2) for it in si])

    #求乘積之和
    pSum=sum([prefs[p1][it]*prefs[p2][it] for it in si])

    #計算皮爾遜評價值
    num=pSum-(sum1*sum2/n)
    den=sqrt((sum1sq-pow(sum1,2)/n)*(sum2sq-pow(sum2,2)/n))
    if den==0:
             return 0
    r=num/den
    return r

該函式將返回一個介於-1和1之間的數值：值為1時，兩個人對同一樣物品均有著一致的評價。與距離度量法不同，此處我們無需為達到正確的比率而對這一數值進行變換。以下程式碼求得圖2-3中的相關評價值：

reload(recommendations)
print(recommendations.sim_person(recommendations.critics,'Lisa Rose','Gene Seymour'))

結果：0.39840953644479793
（五）應該選用哪一種相似性度量方法  Which Similarity Metic Should You Use？
除了上述兩種度量方法，還有許多方法可以衡量兩組資料間的相似程度。哪種方法最優，取決於具體的應用。 本章剩餘部分出現的函式均有一個可選的相似性引數，該引數指向一個實際的演算法函式，這可以使針對演算法的實驗變得更加容易：我們可以指定sim_pearson或sim_distance作為相似性引數的取值。我們還可以使用許多其他的函式，如Jaccard係數或曼哈頓距離演算法，作為相似度計算函式，只要它們滿足如下條件：擁有同樣的函式簽名，以一個浮點數作為返回值，其數值越大代表相似度越大。 Jaccard 係數：又叫Jaccard相似性係數，用來比較樣本集中的相似性和分散性的一個概率。Jaccard係數等於樣本集交集與樣本集合集的比值，即J = |A∩B| ÷ |A∪B|。即樣本交集和樣本並集的比值，兩個文件的共同都有的詞除以兩個文件所有的詞；
Jaccard 距離(Jaccard Distance) ：是用來衡量兩個集合差異性的一種指標，它是傑卡德相似係數的補集，被定義為1減去Jaccard相似係數。 曼哈頓距離(Manhattan Distance)：
曼哈頓距離來源於城市區塊距離，是將多個維度上的距離進行求和後的結果，即當上面的明氏距離中p=1時得到的距離度量公式，如下：