機器學習---特徵選擇
特徵工程是機器學習中不可或缺的一部分,在機器學習領域中佔有非常重要的地位。
特徵工程,是指用一系列工程化的方式從原始資料中篩選出更好的資料特徵,以提升模型的訓練效果。業內有一句廣為流傳的話是:資料和特徵決定了機器學習的上限,而模型和演算法是在逼近這個上限而已。由此可見,好的資料和特徵是模型和演算法發揮更大的作用的前提。
特徵工程通常包括資料預處理、特徵選擇、降維等環節。如下圖所示:
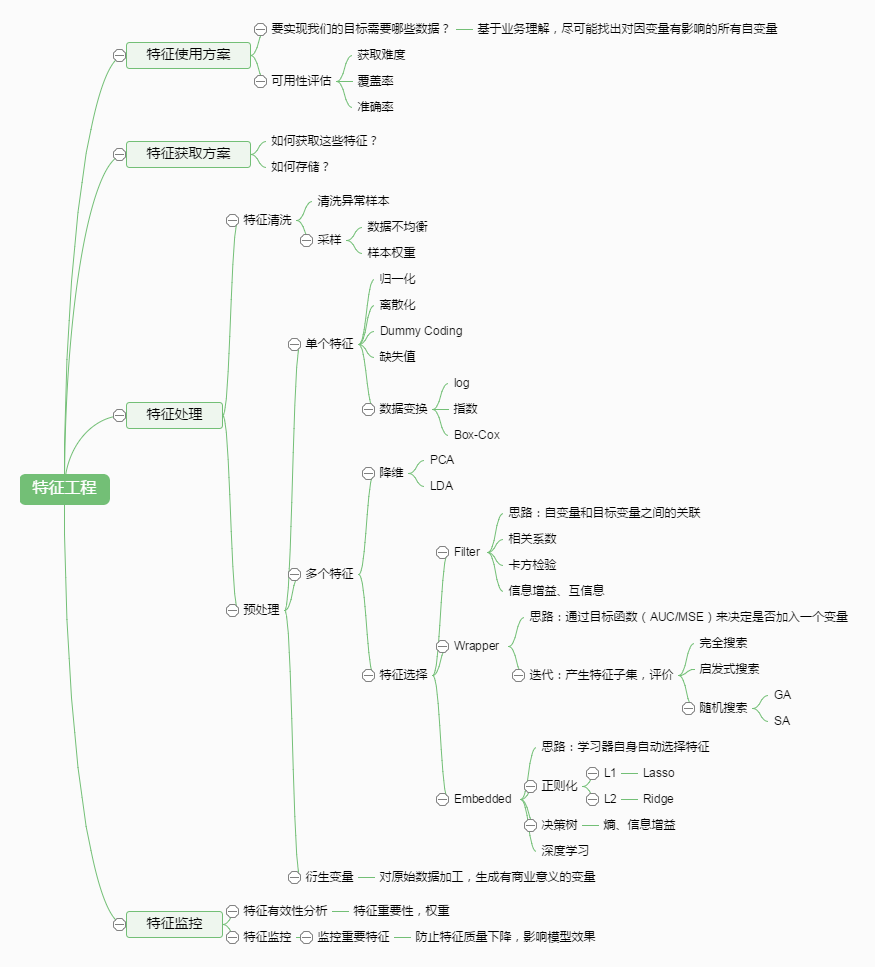
一.資料預處理
資料預處理是特徵工程中最為重要的一個環節,良好的資料預處理可以使模型的訓練達到事半功倍的效果。資料預處理旨在通過歸一化、標準化、正則化等方式改進不完整、不一致、無法直接使用的資料。具體方法有:
- 歸一化
歸一化是對資料集進行區間縮放
- 標準化
標準化是在不改變原資料分佈的前提下,將資料按比例縮放,使之落入一個限定的區間,使資料之間具有可比性。但當個體特徵太過或明顯不遵從高斯正態分佈時,標準化表現的效果會比較差。標準化的目的是為了方便資料的下一步處理,比如:進行的資料縮放等變換。常用的標準化方法有z-score標準化、StandardScaler標準化等。
- 離散化
離散化是把連續型的數值型特徵分段,每一段內的資料都可以當做成一個新的特徵。具體又可分為等步長方式離散化和等頻率的方式離散化,等步長的方式比較簡單,等頻率的方式更加精準,會跟資料分佈有很大的關係。 程式碼層面,可以用pandas中的cut方法進行切分。總之,離散化的特徵能夠提高模型的執行速度以及準確率。
- 二值化
特徵的二值化處理是將數值型資料輸出為布林型別。其核心在於設定一個閾值,當樣本數值大於該閾值時,輸出為1,小於等於該閾值時輸出為0。我們通常使用preproccessing庫的Binarizer類對資料進行二值化處理。
- 啞編碼
我們針對類別型的特徵,通常採用啞編碼(One_Hot Encoding)的方式。所謂的啞編碼,直觀的講就是用N個維度來對N個類別進行編碼,並且對於每個類別,只有一個維度有效,記作數字1 ;其它維度均記作數字0。但有時使用啞編碼的方式,可能會造成維度的災難,所以通常我們在做啞編碼之前,會先對特徵進行Hash處理,把每個維度的特徵編碼成詞向量。
以上為大家介紹了幾種較為常見、通用的資料預處理方式,但只是浩大特徵工程中的冰山一角。往往很多特徵工程的方法需要我們在專案中不斷去總結積累比如:針對缺失值的處理,在不同的資料集中,用均值填充、中位數填充、前後值填充的效果是不一樣的;對於類別型的變數,有時我們不需要對全部的資料都進行啞編碼處理;對於時間型的變數有時我們有時會把它當作是離散值,有時會當成連續值處理等。所以很多情況下,我們要根據實際問題,進行不同的資料預處理。
二.特徵選擇
不同的特徵對模型的影響程度不同,我們要自動地選擇出對問題重要的一些特徵,移除與問題相關性不是很大的特徵,這個過程就叫做特徵選擇。特徵的選擇在特徵工程中十分重要,往往可以直接決定最後模型訓練效果的好壞。常用的特徵選擇方法有:過濾式(filter)、包裹式(wrapper)、嵌入式(embedding)。
- 過濾式
過濾式特徵選擇是通過評估每個特徵和結果的相關性,來對特徵進行篩選,留下相關性最強的幾個特徵。核心思想是:先對資料集進行特徵選擇,然後再進行模型的訓練。過濾式特徵選擇的優點是思路簡單,往往通過Pearson相關係數法、方差選擇法、互資訊法等方法計算相關性,然後保留相關性最強的N個特徵,就可以交給模型訓練;缺點是沒有考慮到特徵與特徵之間的相關性,從而導致模型最後的訓練效果沒那麼好。
- 包裹式
包裹式特徵選擇是把最終要使用的機器學習模型、評測效能的指標作為特徵選擇的重要依據,每次去選擇若干特徵,或是排除若干特徵。通常包裹式特徵選擇要比過濾式的效果更好,但由於訓練過程時間久,系統的開銷也更大。最典型的包裹型演算法為遞迴特徵刪除演算法,其原理是使用一個基模型(如:隨機森林、邏輯迴歸等)進行多輪訓練,每輪訓練結束後,消除若干權值係數較低的特徵,再基於新的特徵集進行新的一輪訓練。
- 嵌入式
嵌入式特徵選擇法是根據機器學習的演算法、模型來分析特徵的重要性,從而選擇最重要的N個特徵。與包裹式特徵選擇法最大的不同是,嵌入式方法是將特徵選擇過程與模型的訓練過程結合為一體,這樣就可以快速地找到最佳的特徵集合,更加高效、快捷。常用的嵌入式特徵選擇方法有基於正則化項(如:L1正則化)的特徵選擇法和基於樹模型的特徵選擇法(如:GBDT)。
三.降維
如果拿特徵選擇後的資料直接進行模型的訓練,由於資料的特徵矩陣維度大,可能會存在資料難以理解、計算量增大、訓練時間過長等問題,因此我們要對資料進行降維。降維是指把原始高維空間的特徵投影到低維度的空間,進行特徵的重組,以減少資料的維度。降維與特徵最大的不同在於,特徵選擇是進行特徵的剔除、刪減,而降維是做特徵的重組構成新的特徵,原始特徵全部“消失”了,性質發生了根本的變化。
常見的降維方法有:主成分分析法(PCA)和線性判別分析法(LDA)。
- 主成分分析法
主成分分析法(PCA)是最常見的一種線性降維方法,其要儘可能在減少資訊損失的前提下,將高維空間的資料對映到低維空間中表示,同時在低維空間中要最大程度上的保留原資料的特點。主成分分析法本質上是一種無監督的方法,不用考慮資料的類標,它的基本步驟大致如下:
- 資料中心化(每個特徵維度減去相應的均值)
- 計算協方差矩陣以及它的特徵值和特徵向量
- 將特徵值從大到小排序並保留最上邊的N個特徵
- 將高維資料轉換到上述N個特徵向量構成的新的空間中
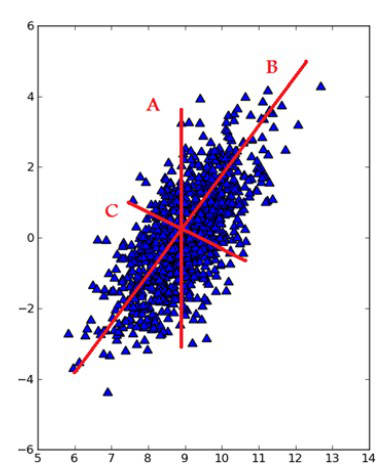
此外,在把特徵對映到低維空間時要注意,每次要保證投影維度上的資料差異性最大(也就是說投影維度的方差最大)。我們可以通過圖1-5來理解這一過程:
- 線性判別分析法
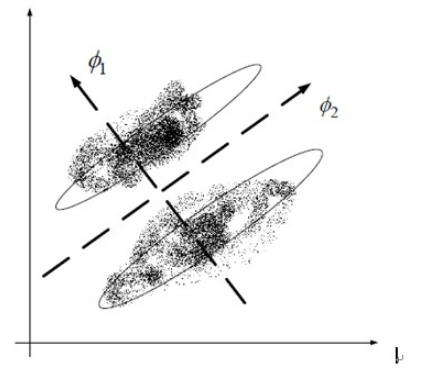
線性判別分析法(LDA)也是一種比較常見的線性降維方法,但不同於PCA的是,它是一種有監督的演算法,也就是說它資料集的每個樣本會有一個輸出類標。線性判別演算法的核心思想是,在把資料投影到低維空間後,希望同一種類別數據的投影點儘可能的接近,而不同類別資料的類別中心之間的距離儘可能的遠。也就是說LDA是想讓降維後的資料點儘可能地被區分開。其示例圖如下所示:
以上為大家總結了常用的一些特徵工程方法,我們可以使用sklearn完成幾乎所有特徵處理的工作,具體參考:
