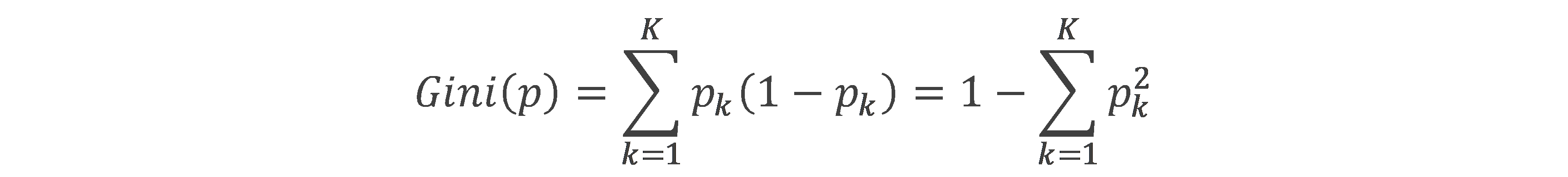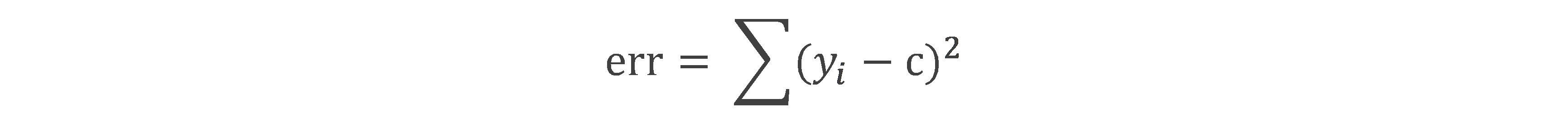CART分類與迴歸樹本質上是一樣的，構建過程都是逐步分割特徵空間，預測過程都是從根節點開始一層一層的判斷直到葉節點給出預測結果。只不過分類樹給出離散值，而回歸樹給出連續值(通常是葉節點包含樣本的均值），另外分類樹基於Gini指數選取分割點，而回歸樹基於平方誤差選取分割點。

CART分類樹：

核心思想：以特徵及對應特徵值為切分點，逐步切分特徵空間

基本概念：

基尼指數(Gini):樣本屬於第K類的概率為pk，則基尼指數為

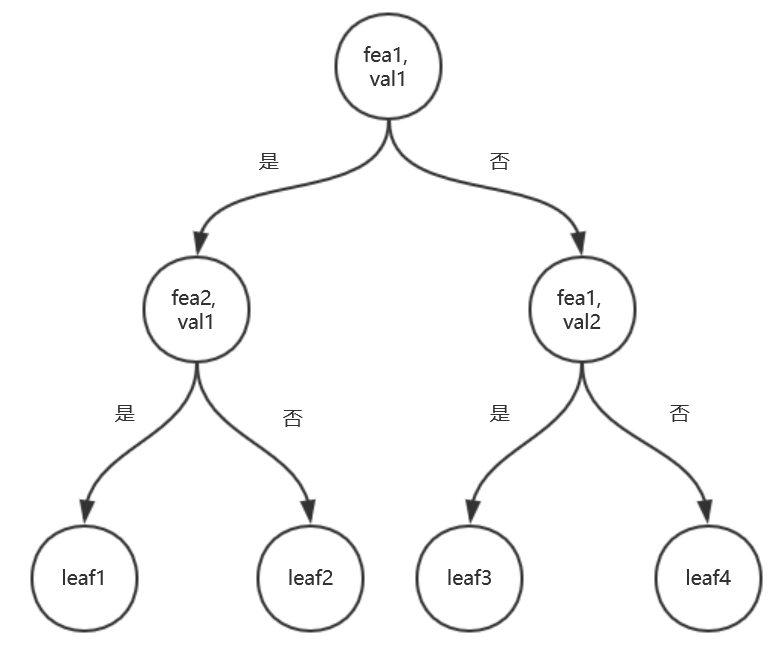
CART分類樹示意圖如下：

演算法流程：

l  Input：閾值epsilon，最少樣本量min_sample，訓練資料集X，y

l  Output: CART分類樹

l  Step1：建立特徵集，空樹。

l  Step2: 遞迴構建樹。

遞迴終止條件：

        1.     子資料集少於閾值min_sample

        2.     基尼指數下降量少於epsilon

       樹的構建流程：

        1.     搜尋最優切分點(由特徵及某個值的元組構成)，並返回切分後兩個子資料集的索引。

        2.     依據最優切分點構建樹的節點，其中滿足切分點條件為左子樹，反之右子樹。

        3.     重複步驟1，2，遞迴切分兩個子資料集。

l  Step3: 運用構建好的分類樹預測。遞迴搜尋樹，碰到葉節點返回標記。

"""
CART分類樹，是一顆二叉樹，以某個特徵以及該特徵對應的一個值為節點，故相對ID3演算法，最大的不同就是特徵可以使用多次
"""
from collections import Counter, defaultdict

import numpy as np


class node:
    def __init__(self, fea=-1, val=None, res=None, right=None, left=None):
        self.fea = fea  # 特徵
        self.val = val  # 特徵對應的值
        self.res = res  # 葉節點標記
        self.right = right
        self.left = left


class CART_CLF:
    def __init__(self, epsilon=1e-3, min_sample=1):
        self.epsilon = epsilon
        self.min_sample = min_sample  # 葉節點含有的最少樣本數
        self.tree = None

    def getGini(self, y_data):
        # 計算基尼指數
        c = Counter(y_data)
        return 1 - sum([(val / y_data.shape[0]) ** 2 for val in c.values()])

    def getFeaGini(self, set1, set2):
        # 計算某個特徵及相應的某個特徵值組成的切分節點的基尼指數
        num = set1.shape[0] + set2.shape[0]
        return set1.shape[0] / num * self.getGini(set1) + set2.shape[0] / num * self.getGini(set2)

    def bestSplit(self, splits_set, X_data, y_data):
        # 返回所有切分點的基尼指數，以字典形式儲存。鍵為split，是一個元組，第一個元素為最優切分特徵，第二個為該特徵對應的最優切分值
        pre_gini = self.getGini(y_data)
        subdata_inds = defaultdict(list)  # 切分點以及相應的樣本點的索引
        for split in splits_set:
            for ind, sample in enumerate(X_data):
                if sample[split[0]] == split[1]:
                    subdata_inds[split].append(ind)
        min_gini = 1
        best_split = None
        best_set = None
        for split, data_ind in subdata_inds.items():
            set1 = y_data[data_ind]  # 滿足切分點的條件，則為左子樹
            set2_inds = list(set(range(y_data.shape[0])) - set(data_ind))
            set2 = y_data[set2_inds]
            if set1.shape[0] < 1 or set2.shape[0] < 1:
                continue
            now_gini = self.getFeaGini(set1, set2)
            if now_gini < min_gini:
                min_gini = now_gini
                best_split = split
                best_set = (data_ind, set2_inds)
        if abs(pre_gini - min_gini) < self.epsilon:  # 若切分後基尼指數下降未超過閾值則停止切分
            best_split = None
        return best_split, best_set, min_gini

    def buildTree(self, splits_set, X_data, y_data):
        if y_data.shape[0] < self.min_sample:  # 資料集小於閾值直接設為葉節點
            return node(res=Counter(y_data).most_common(1)[0][0])
        best_split, best_set, min_gini = self.bestSplit(splits_set, X_data, y_data)
        if best_split is None:  # 基尼指數下降小於閾值，則終止切分，設為葉節點
            return node(res=Counter(y_data).most_common(1)[0][0])
        else:
            splits_set.remove(best_split)
            left = self.buildTree(splits_set, X_data[best_set[0]], y_data[best_set[0]])
            right = self.buildTree(splits_set, X_data[best_set[1]], y_data[best_set[1]])
            return node(fea=best_split[0], val=best_split[1], right=right, left=left)

    def fit(self, X_data, y_data):
        # 訓練模型，CART分類樹與ID3最大的不同是，CART建立的是二叉樹，每個節點是特徵及其對應的某個值組成的元組
        # 特徵可以多次使用
        splits_set = []
        for fea in range(X_data.shape[1]):
            unique_vals = np.unique(X_data[:, fea])
            if unique_vals.shape[0] < 2:
                continue
            elif unique_vals.shape[0] == 2:  # 若特徵取值只有2個，則只有一個切分點，非此即彼
                splits_set.append((fea, unique_vals[0]))
            else:
                for val in unique_vals:
                    splits_set.append((fea, val))
        self.tree = self.buildTree(splits_set, X_data, y_data)
        return

    def predict(self, x):
        def helper(x, tree):
            if tree.res is not None:  # 表明到達葉節點
                return tree.res
            else:
                if x[tree.fea] == tree.val:  # "是" 返回左子樹
                    branch = tree.left
                else:
                    branch = tree.right
                return helper(x, branch)

        return helper(x, self.tree)

    def disp_tree(self):
        # 列印樹
        self.disp_helper(self.tree)
        return

    def disp_helper(self, current_node):
        # 前序遍歷
        print(current_node.fea, current_node.val, current_node.res)
        if current_node.res is not None:
            return
        self.disp_helper(current_node.left)
        self.disp_helper(current_node.right)
        return


if __name__ == '__main__':
    from sklearn.datasets import load_iris

    X_data = load_iris().data
    y_data = load_iris().target


    import time
    from machine_learning_algorithm.cross_validation import validate
    start = time.clock()

    g = validate(X_data, y_data, ratio=0.2)
    for item in g:
        X_data_train, y_data_train, X_data_test, y_data_test = item
        clf = CART_CLF()
        clf.fit(X_data_train, y_data_train)
        score = 0
        for X, y in zip(X_data_test,y_data_test):
            if clf.predict(X) == y:
                score += 1
        print(score / len(y_data_test))
    print(time.clock() - start)
 

CART迴歸樹：

核心思想：CART迴歸樹樣本空間細分成若干子空間，子空間內樣本的輸出y(連續值)的均值即為該子空間內的預測值。故對於輸入X為一維時，預測結果可表示為階梯函式。

基本概念：平方誤差：yi 屬於某個資料集，c為該資料上輸出向量y的均值。

演算法流程：

Input：閾值epsilon，最少樣本量min_sample，訓練資料集X，y

Output: CART迴歸樹

l  Step1: 構建特徵集，空樹

l  Step2: 遞迴構建二叉樹。

        遞迴終止條件：

        1.     子資料集大小小於min_sample

        2.     切分後存在子資料集大小不足2

        3.     切分後兩個子資料集的平方誤差和小於epsilon

        樹的構建流程：

        1.     以每個特徵j及相應的取值s為切分點，將資料集劃分成左右兩個子資料集，計算兩個子資料集的平方誤差。

        2.     取平方誤差最小的（j, s）,構建二叉樹的節點

        3.     呼叫步驟1，2，遞迴對兩個子資料集劃分

l  Step3: 預測

"""
CART+最小二乘法構建CART迴歸樹
"""

import numpy as np


class node:
    def __init__(self, fea=-1, val=None, res=None, right=None, left=None):
        self.fea = fea
        self.val = val
        self.res = res
        self.right = right
        self.left = left


class CART_REG:
    def __init__(self, epsilon=0.1, min_sample=10):
        self.epsilon = epsilon
        self.min_sample = min_sample
        self.tree = None

    def err(self, y_data):
        # 子資料集的輸出變數y與均值的差的平方和
        return y_data.var() * y_data.shape[0]

    def leaf(self, y_data):
        # 葉節點取值，為子資料集輸出y的均值
        return y_data.mean()

    def split(self, fea, val, X_data):
        # 根據某個特徵，以及特徵下的某個取值，將資料集進行切分
        set1_inds = np.where(X_data[:, fea] <= val)[0]
        set2_inds = list(set(range(X_data.shape[0]))-set(set1_inds))
        return set1_inds, set2_inds

    def getBestSplit(self, X_data, y_data):
        # 求最優切分點
        best_err = self.err(y_data)
        best_split = None
        subsets_inds = None
        for fea in range(X_data.shape[1]):
            for val in X_data[:, fea]:
                set1_inds, set2_inds = self.split(fea, val, X_data)
                if len(set1_inds) < 2 or len(set2_inds) < 2:  # 若切分後某個子集大小不足2，則不切分
                    continue
                now_err = self.err(y_data[set1_inds]) + self.err(y_data[set2_inds])
                if now_err < best_err:
                    best_err = now_err
                    best_split = (fea, val)
                    subsets_inds = (set1_inds, set2_inds)
        return best_err, best_split, subsets_inds

    def buildTree(self, X_data, y_data):
        # 遞迴構建二叉樹
        if y_data.shape[0] < self.min_sample:
            return node(res=self.leaf(y_data))
        best_err, best_split, subsets_inds = self.getBestSplit(X_data, y_data)
        if subsets_inds is None:
            return node(res=self.leaf(y_data))
        if best_err < self.epsilon:
            return node(res=self.leaf(y_data))
        else:
            left = self.buildTree(X_data[subsets_inds[0]], y_data[subsets_inds[0]])
            right = self.buildTree(X_data[subsets_inds[1]], y_data[subsets_inds[1]])
            return node(fea=best_split[0], val=best_split[1], right=right, left=left)

    def fit(self, X_data, y_data):
        self.tree = self.buildTree(X_data, y_data)
        return

    def predict(self, x):
        # 對輸入變數進行預測
        def helper(x, tree):
            if tree.res is not None:
                return tree.res
            else:
                if x[tree.fea] <= tree.val:
                    branch = tree.left
                else:
                    branch = tree.right
                return helper(x, branch)

        return helper(x, self.tree)


if __name__ == '__main__':
    import matplotlib.pyplot as plt

    X_data_raw = np.linspace(-3, 3, 50)
    np.random.shuffle(X_data_raw)
    y_data = np.sin(X_data_raw)
    X_data = np.transpose([X_data_raw])
    y_data = y_data + 0.1 * np.random.randn(y_data.shape[0])
    clf = CART_REG(epsilon=1e-4, min_sample=1)
    clf.fit(X_data, y_data)
    res = []
    for i in range(X_data.shape[0]):
        res.append(clf.predict(X_data[i]))
    p1 = plt.scatter(X_data_raw, y_data)
    p2 = plt.scatter(X_data_raw, res, marker='*')
    plt.legend([p1,p2],['real','pred'],loc='upper left')
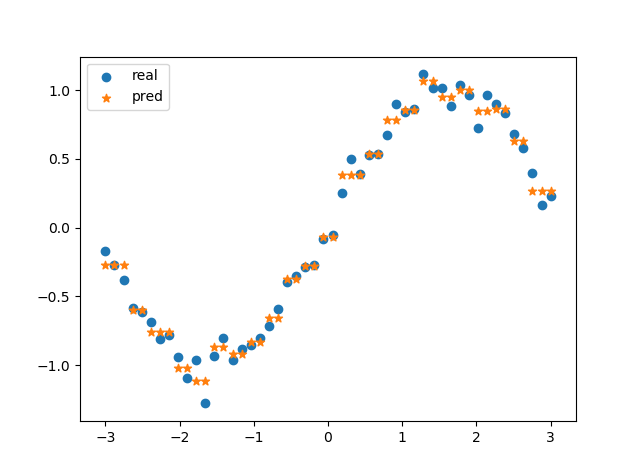
    plt.show()

預測結果示例：

[我的GitHub](https://github.com/Shi-Lixin)
注：如有不當之處，請指正。