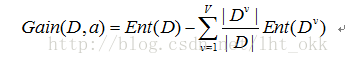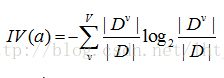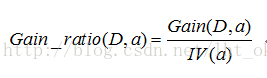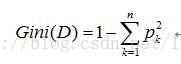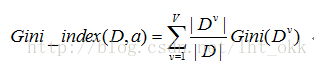決策樹(decision tree)的自我理解 (上)
最近在看周志華的《機器學習》,剛好看完決策樹這一章,因此結合網上的一些參考資料寫一下自己的理解。
何為決策樹?
決策樹是一種常見機器學習方法中的一種分類器。它通過訓練資料構建一種類似於流程圖的樹結構,其中每個內部結點表示在一個屬性上的測試對未知資料進行分類,每個分支代表一個屬性輸出,每個樹葉結點代表類或類分佈。
決策樹包括:根結點、若干個內部結點、若干個葉節點(即目標分類節點)。
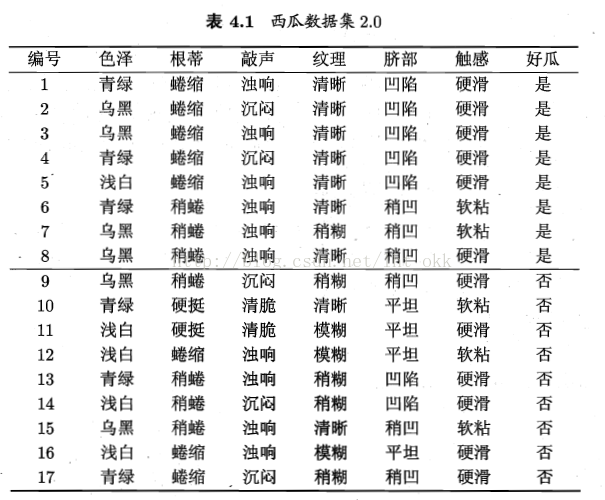
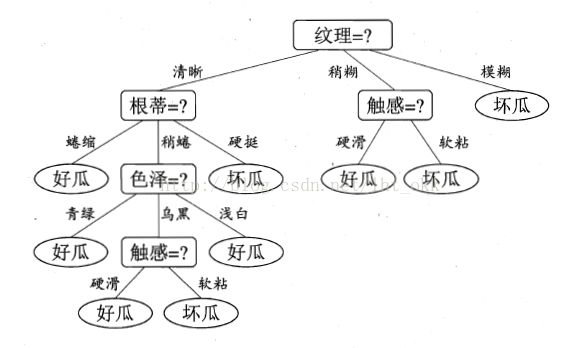
如以下資料集生成決策樹:
決策樹與其他分類演算法相比的優缺點
優點:
1.直觀,決策樹可以提供視覺化,便於理解;
2.適用於小規模資料;
3.資料的準備往往是簡單或者不必要的,
4.對相關特徵資料的處理;
缺點:
1.連續變數處理不好,也就是說當資料中存在連續變數的屬性時,決策樹表現並不是很好;
2.特徵屬性增加時,錯誤增加的比較快;
3.不穩定性,一點點的擾動或者改動都可能改動整棵樹,我們想要的分類器對噪聲是健壯的
4.當資料出現不相關的特徵,表現不是很好。
5. 很容易在訓練資料中生成複雜的樹結構,造成過擬合(overfitting)。
決策樹演算法流程
輸入:- 資料分割槽D,訓練元組和它們對應類標號的集合。
- attribute_list,候選屬性的集合
- Attribute_selection_method,一個確定“”最好的“劃分資料元組為個體類的分裂準則的過程,這個準側由分裂屬性(splitting_attribute)和分裂點或劃分子集組成。
- 選擇一個特徵節點建立一個根結點N (下面步驟則是在N下新增結點,最終形成一棵樹N)
- if D中的元組都在同一類C中 then 返回N作為葉節點,以類C標記;
- if attribute_list 為空 then 返回D作為葉節點,標記為D中的多數類;
- 使用Attribute_selection_method(D,attribute_list)找出最好的(多數表決)splitting_criterion(分類標準)的特徵;
- 使用該特徵標記結點N;
- if splitting_criterion(符合該特徵的特徵) 為離散值,允許多路劃分,then attribute_list = attribute_list - splitting_criterion (從候選集合裡刪除已選擇過的屬性)
- for j in splitting_criterion (遍歷splitting_criterion裡的每一種分類切割出來的子集)
- Dj為D中滿足輸出j的資料元組的集合;
- if Dj為空 then 加一個樹葉結點N,標記為D中的多數類
- else 加一個由Generate_decision_tree(D,attribute_list)返回的結點到N;(也就是由下面的D的attribute_list繼續分割產生結點接到樹下面)
- 返回N(決策樹)
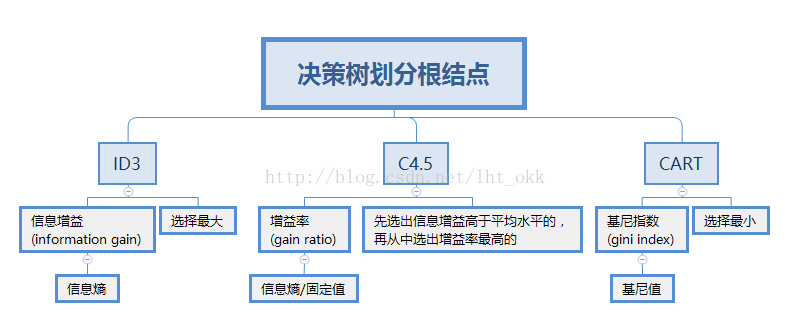
重點:如何選擇節點Attribute_selection_method
根據選擇節點所應用的演算法不同,因此決策樹也通常分三種討論,介紹下基本的三種分列準則。
總的來說就是
分兩部分講解
一、計算公式的實現
ID3決策樹:
資訊熵
計算整個資料集D的資訊熵,對資料集中每個類別k計算概率,即該類別佔總體的比例,一共有n類。越小,D的純度越高。
資訊增益
計算屬性a的資訊增益,對總體資料集D根據屬性a進行劃分子集,總共V的子集, 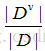
C4.5決策樹
固定值
增益率
CART決策樹
CART演算法採用一種二分遞迴分割的技術,將當前的樣本集分為兩個子樣本集,使得生成的的每個非葉子節點都有兩個分支。因此,CART演算法生成的決策樹是結構簡潔的二叉樹。
基尼值
基尼指數
基尼指數考慮的是每個屬性的二元劃分,因此在當屬性值A分類(假如有v類)超過2個時,考慮將屬性A二元劃分,在不考慮全集和空集的情況下,一共有2^v-2個劃分方法。對於每個屬性,考慮每種可能的二元劃分。對於屬性A,選擇屬性產生最小基尼指數的子集作為作為它的分列子集。
二、各演算法之間的比較
ID3(Iterative Dichotomiser 3,迭代二叉樹3代)由Ross Quinlan於1986年提出。1993年,他對ID3進行改進設計出了C4.5演算法。
ID3演算法缺點:資訊增益會讓ID3演算法更偏向於選擇值多的屬性。資訊增益反映給定一個條件後不確定性減少的程度,必然是分得越細的資料集確定性更高,也就是資訊熵越小,資訊增益越大。因此,在一定條件下,值多的屬性具有更大的資訊增益。
C4.5演算法:在ID3基礎上提出,試圖克服這種ID3的缺點,用固定值IV(a)將資訊增益規範化。
如果劃分的資訊熵值非常小,資訊增益率將會不穩定.因此,C4.5系統中引入一個限制來解決這個問題:待選測試的資訊增益值不能小於所有的檢測過的測試的平均資訊增益值。如果屬性集中存在無關屬性,即便該屬性沒有被選為測試屬性,都將影響資訊增益率的效果.因為引進的無關屬性會降低測試的資訊增益的平均值,所以一些具有高資訊增益率而低資訊增益的屬性將成為最優的測試屬性.這種情況就不會在使用資訊增益函式的決策樹中出現.實際應用說明資訊增益率函式比資訊增益函式更健壯,能穩定地選擇好的測試。
CART(Classification And Regression Tree,分類迴歸樹)由L.Breiman,J.Friedman,R.Olshen和C.Stone於1984年提出,是一種應用相當廣泛的決策樹學習方法。值得一提的是,CART和C4.5一同被評為資料探勘領域十大演算法。
參考:《機器學習》--周志華
《資料探勘:概念與技術》 -- Jiawei Han
最後
其實關於決策樹的知識,這裡還差個剪枝部分和決策樹關於連續值和缺失值的處理這三部分的知識,在下一篇做下自我理解吧。有什麼講的不是很好,甚至錯誤的地方請大家幫我指出,謝謝!!
進步始於交流,收穫源於分享,願意分享的心,感恩回饋的心!