線性代數學習筆記3
第五集 向量空間
我們可以對向量進行所謂“線性運算”,即通過加和(v+w)與數乘運算(3v)得到向量的線性組合。向量空間對線性運算封閉,即空間內向量進行線性運算得到的向量仍在空間之內。
包含於向量空間之內的一個向量空間稱為原向量空間的一個子空間。
•
• 過原點的一條直線(這是
• 原點 僅包含0 向量
•
• 過原點的一個平面 2 維
• 過原點的一條直線 1 維
• 原點 僅包含0 向量
第六集 列空間和零空間
列空間
矩陣A 的列空間C(A)是其列向量的所有線性組合所構成的空間。
求解Ax=b 的問題,對於給定的矩陣A,對於任意的b 都能得到解麼?
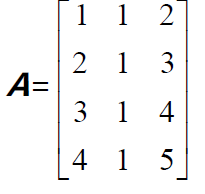
矩陣A 列向量的線性組合無法充滿
而且,由於列向量不是線性無關的(第三個列向量為前兩個列向量之和),所以儘管有3 個列向量,但是隻有2 個對張成向量空間有貢獻。矩陣A 的列空間為
零空間
矩陣A 的零空間N(A)是指滿足Ax=0 的所有解的集合。x 為含有3 個分量的向量,故矩陣A 的零空間是
若方程變為

則其解集不能構成一個子空間。零向量並不在這個集合內。
對於列空間,它是由列向量進行線性組合張成的空間;而零空間是從方程組出發,通過讓x 滿足特定條件而得到的子空間。
第七集 求解Ax=0:主變數,特解
計算零空間,矩陣A 的零空間即滿足Ax=0 的所有x構成的向量空間。
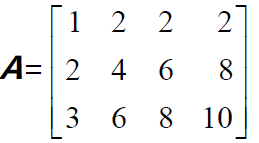
對於矩陣A 進行“行操作”並不會改變Ax=b 的解,因此也不會改變零空間(但是會改變列空間)。消元得到
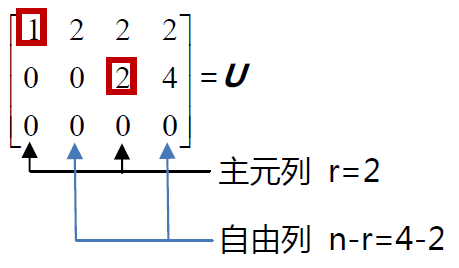
矩陣U 為梯形矩陣。其第三行變為零,是因為第三行的行向量本身就是第一行和第二行行向量的線性組合。矩陣的秩r就是矩陣的主元的個數,表示只有r個方程起作用。
當我們將係數矩陣變換為上三角陣U 時,就可以用回代求得方程Ux=0 的解。
本例中,包含主元的矩陣第1 列和第3 列為主元列,而不包含主元的第2 列和第4列為自由列。對自由變數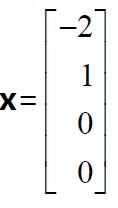
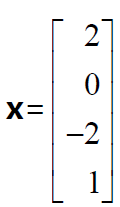
矩陣A 的零空間就是這些“特解”向量的線性組合所構成的向量空間,
自由列可以表示為其左側所有主元列的線性組合。

觀察它的第五列自由列,其左側有兩個主元列,這兩個主元列線性無關,第五列顯然可以寫成前兩個主元列的線性組合。求Ux=0 的解,如果令其他所有自由列的x 分量都為0,而
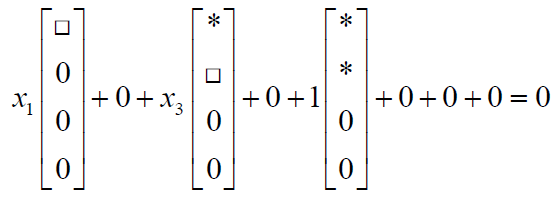
相當於求第五列如何用前兩個主元列進行線性組合,所得解
行最簡階梯矩陣
行最簡階梯矩陣形式R,其中主元為1,而主元列除主元外皆為0。
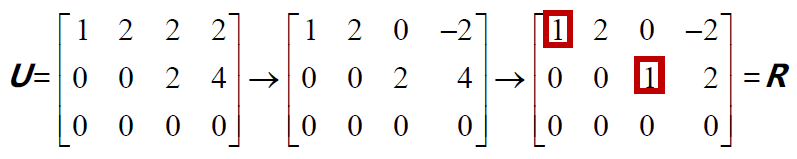
通過“列交換”,可以將矩陣R 中的主元列集中在左側,從而在左上角形成這個單位陣。如果矩陣A 中的某些行是線性相關的,則在矩陣R 的下半部分就會出現一些完全為0的行向量。F即自由列消元后組成的部分。
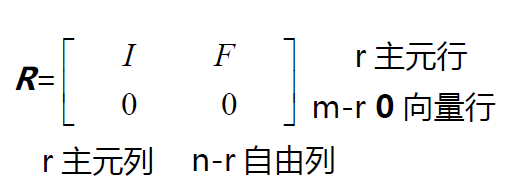
原方程Ax=0 變為Ux=0,又變為求解Rx=0。
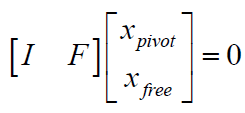
回代得
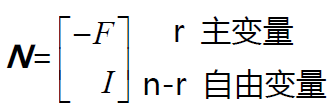
此時要注意如果在變換出R 左上角的單位陣的過程中採用了列交換,則最後的解要完成逆變換。在本例中,R進行了第二列和第三列交換才形成
第八集 求解Ax=b:可解性和解的結構
可解的條件
取A為上一講中的矩陣,則
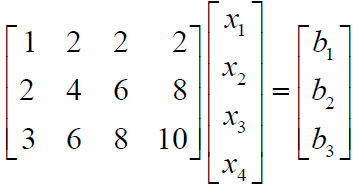
矩陣A 的第三行為第一行和第二行的加和,因此Ax=b 中b 的第3 個分量也要等於其第1 和第2 個分量的和,即只有當b 處於矩陣的列空間C(A)之中時,方程才有解。
對增廣矩陣進行行消元,如下圖所示。如果Ax=b 有解,則b3-b1-b2=0。

在本例中我們令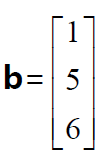
特解:求Ax=b 特解的方法是將自由變數均賦值為0,求解其主變數。令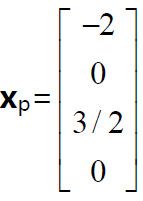

對於Ax=b的求解轉變為Ux=c。此時四個主元列的線性組合可以組成任何
與零空間進行線性組合
Ax=b 的通解為
