本部落格僅用來記錄重要概念。

線性代數學習請移步https://www.bilibili.com/video/av6731067

不得不說，這位up主講的是真心好，尤其是點積叉積那一部分，直接重新整理世界觀QWQ。

基

空間內的一組基指的是：張成該空間的一個線性無關向量的集合

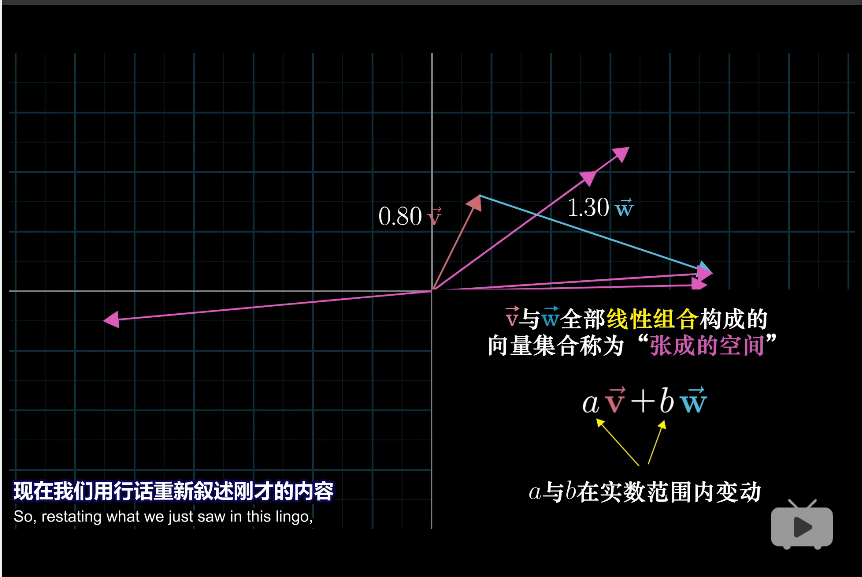
張成

所有可以表示為給定向量線性組合的向量的集合被稱為給定向量張成的空間

張成在這裡應該是動詞。

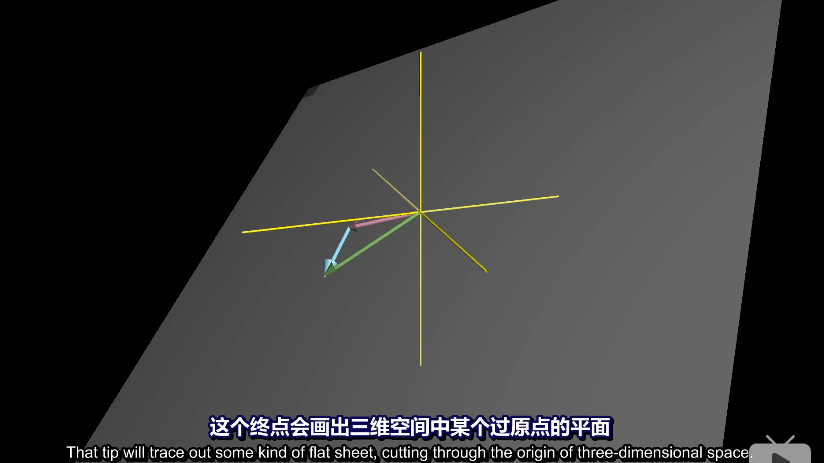
在三維空間中，兩個向量張成出的空間應該是某個過原點的平面

線性相關

一組向量中至少有一個是多餘的，沒有對張成空間做出任何貢獻

你有多個向量， 並且可以移除其中的一個而不減小張成的空間

這種情況發生時，我們稱他們是“線性相關”的

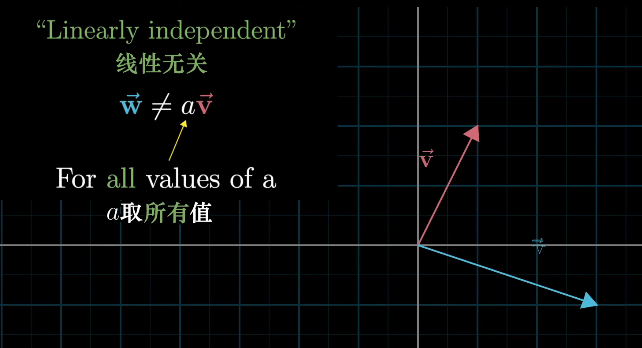
如果所有的向量都給張成的空間增加了新的維度，他們就被稱為“線性無關”

矩陣

這介紹怎麼這麼鬼畜。。

對空間的一種特定變換

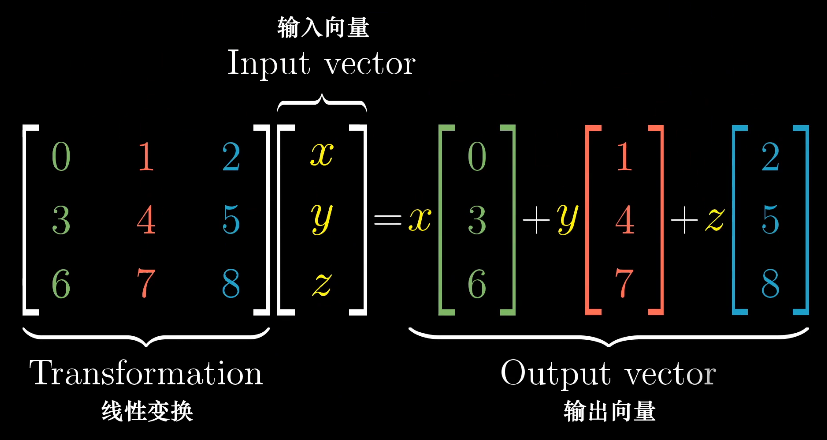
線性變換

接收一個向量，並輸出一個向量的變換

線性的直觀含義：

1.直線在變換後仍然為直線，不能有所彎曲

2.原點必須保持固定（如果原點不固定，它可能為“仿射變換”）

注意：線性變換“保持網格線平行且等距分佈”—》如果變換前的向量是$i$和$j$的線性組合，那麼變換後也是$i$和$j$的線性組合

矩陣乘法

複合矩陣

乘積需要從右往左計算

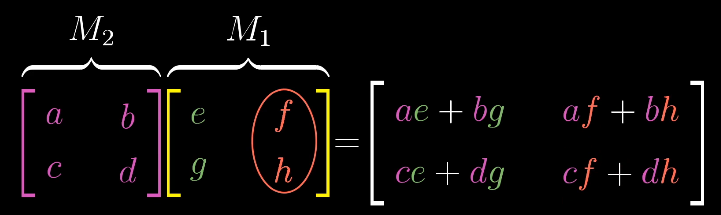
我對矩陣乘法的理解：

首先把$M_1$的$[e,g]$看成一個向量，$[f,h]$看成一個向量

左乘$M_2$實際是兩個向量分別與$M_2$相乘

$M_2$可以看做將基底進行變換的矩陣

根據線性變換的性質，

$[e,g]$所代表的向量為$ei + gj$，此時$i$變為$(a,c)$，$j$變為$(b, d)$

然後帶入相乘就得到了最終答案

矩陣乘法的性質

不滿足交換律

對於變換$A,B$，先應用$A$再應用$b$

和線應用$B$，再應用$A$，得到的結果是不同的

滿足結合律

$(AB)C$相當於先應用$C$變換，再應用$B$、$A$變換

$A(BC)$相當於先應用$C$、$B$變換，再應用$A$變換，

他們的運算順序是相同的

三維空間內的線性變換

本質與二維是相同的

行列式

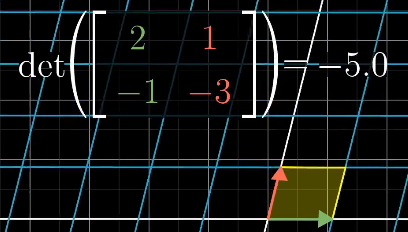
二維空間

線性變換改變面積的比例被稱為這個變換的行列式

當空間定向改變的情況發生時行列式為負

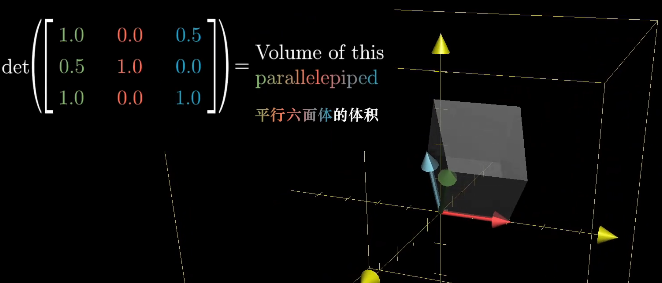
三維空間

三維空間下行列式的值為平行六面體的體積

判斷正負的方法：

右手定則：讓食指指向$i$，中指指向$j$，拇指指向$k$，如果變換之後仍然能這麼做，則為正；若只能用食指這麼做，則為負

行列式的計算

二維

證明：

三維：

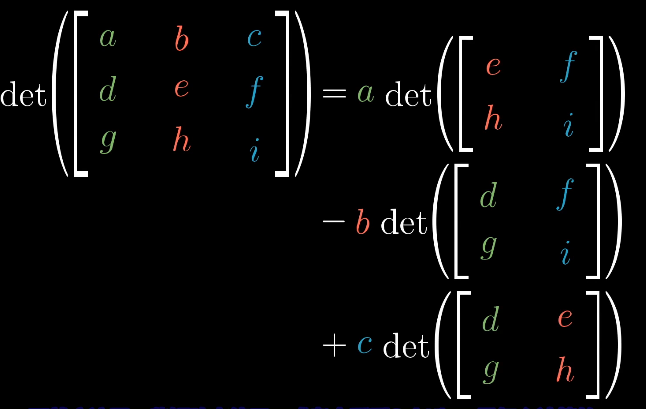
性質

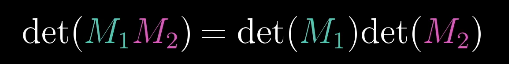
逆矩陣

矩陣的秩

秩：變換後空間的維數/列空間的維數

滿秩：秩與列數相同

列空間

直線/平面/三維空間等，所有可能的變換結果的集合，被稱為矩陣的“列空間”

零空間

零空間：變換後落在原點的向量的集合

點積

定義：

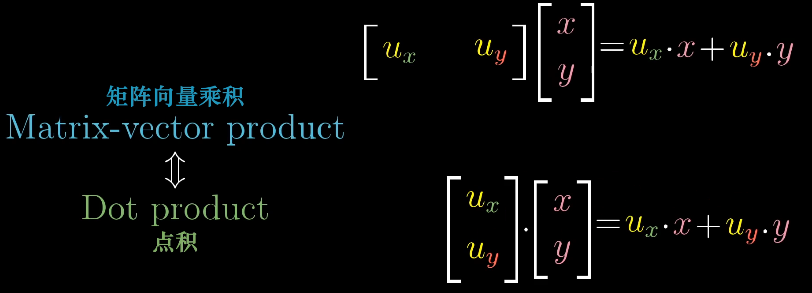
代數：對於兩個維度相同的矩陣，其點積為將相應座標配對，求出每一對座標的乘積再相加

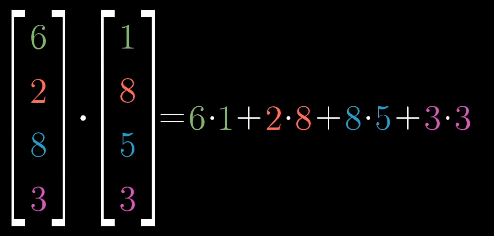
幾何：兩個向量的點積為一個向量在另一個向量上正交投影的長度乘以另一個向量的長度(好繞。。)

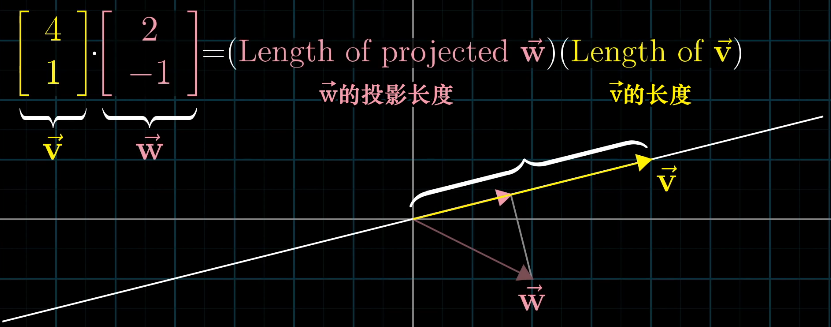
若兩向量反向，則乘積為負

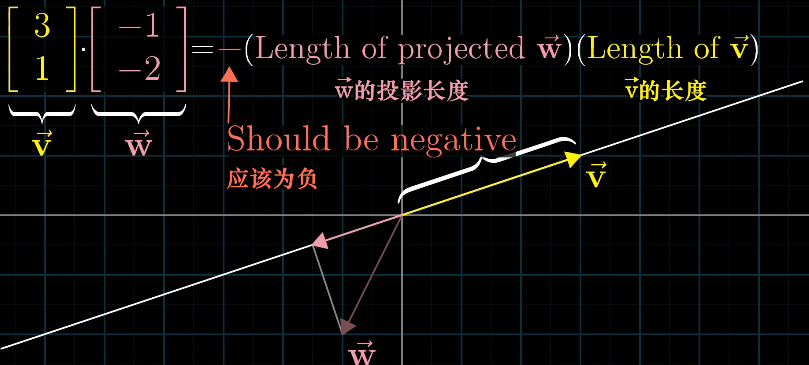
兩者的關係：

這一部分聽傻了，感覺都是神仙推導。太強了orz

叉積

定義

視訊中並沒有明確的給出叉積的定義

大概就是算出兩個向量的行列式來構成第三個向量

正負

對於$i \times j$，若$i$在$j$右側，則叉積為正，否則叉積為負

計算

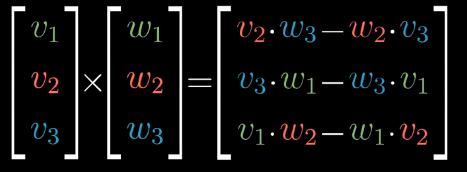
基變換

感覺前面講過。。

特徵向量與特徵值

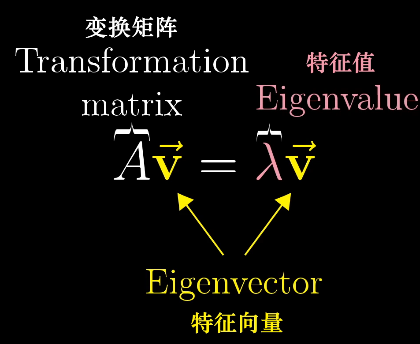
定義

特徵向量

在基向量變換後張成出的空間與基向量不變時張成出的空間相同的向量？

特徵值

特徵向量在變換後被縮放/拉伸的比例