作者：sky sailing

在學概率統計之前，我們學習的都是確定的函式。概率統計討論了一次取值時獲得的值是不確定的，而隨機過程討論了不確定會發生哪個時間函式。

每個小x（t）函式（樣本函式）就是實際發生的一個表示式確定的函式，對每個小x（t）的處理，都是與之前確定函式的處理方法相同的，但是由於我們沒法確定某次究竟發生哪個確定表示式的小x（t），所以我們只能研究發生哪種情況的概率大些，或者當這件事多次發生時，呈現出來的統計特性是什麼。雖然每個小x（t）的特性是不定的，但小x（t）的統計特性卻是確定的，所以我們研究的還是變中的不變數。

學習隨機過程時困擾我的一個基本式子是自相關函式。我開始一直不明白為什麼要用E{X（t1）X(t2)}來表現函式變化的劇烈程度。我一開始不明白具體操作代入時X(t1)和X（t2）應該代入什麼，是在不同的小x（t）上取兩個時刻的值相乘？還是在同一個小x(t)上取兩個時刻的值相乘。後來我又仔細看了一下書上的例子，那個例子用了兩張圖，一張是每個小x（t）變化都很緩，另一張是每個小x（t）變化都很起伏劇烈。但是兩個隨機過程的均值和方差是相同的。書上說均值和方差只刻畫隨機過程X（t）在各個獨立時刻的概率統計特性，反映不了隨機過程的內在相關性，所以引入了自相關函式。從引入自相關函式的目的看來，它是為了分辨形狀不同的小x（t），所以代入E{X（t1）X(t2)}公式的值應該是每個小x（t）上取兩個時刻的函式值自己相乘，這樣才能反映小x（t）的差異。而因為前面所說，我們面對的不是一定會發生的某個小x（t），而是一組均可能發生的小x（t）。所以應該對每個樣本函式取兩個時刻的值函式值相乘後做統計平均來獲得這一組樣本函式的統計特性，或說是平均特性。在這裡我想說一下自己對於統計平均曾經的錯誤理解和修正。物理實驗處理資料時，我們求的都是算術平均，即每個記錄值的權重是相同的。然而求期望時，我們算的是加權平均。看似矛盾但實則相同。這是因為算術平均時若是數值相同的數出現多次，那麼這個數就被重複的代入多次，事實上某數出現的頻率就是它的權重。而當引入概率密度函式時，因為橫軸上的x是不會出現重複的值的，所以要用頻率來做縱座標表現某個x出現可能性的大小。

假設實際發生了n個樣本函式（在實際工程中不可能測無窮組資料，只能是測n組資料認為已經包羅永珍了），分別為<img src="https://pic4.zhimg.com/263d26176c80ad50d7df42b8a31ff6a3_b.png" data-rawwidth="134" data-rawheight="24" class="content_image" width="134">，這n個樣本函式是可以出現表示式（形狀樣子）相同的，但是下標仍是各不相同，在這種前提下每個樣本函式的權值是相同的。所以X（t）的自相關函式的表示式就應為：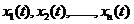

，這n個樣本函式是可以出現表示式（形狀樣子）相同的，但是下標仍是各不相同，在這種前提下每個樣本函式的權值是相同的。所以X（t）的自相關函式的表示式就應為：

<img src="https://pic3.zhimg.com/ac1b44d4c4d3808b60d0f9d7b37ed442_b.png" data-rawwidth="384" data-rawheight="42" class="content_image" width="384">

應該注意的是樣本函式下標的對應關係。

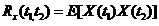我認為比起<img src="https://pic4.zhimg.com/95d0123e63db373625a52f249c61288b_b.png" data-rawwidth="159" data-rawheight="26" class="content_image" width="159">，上邊的具體操作式子才更為重要，因為它體現了自相關函式真正想表達的含義。因為自相關函式在實際工程中是被測出來，再擬合成某個數學表示式的，而不像題目中直接告訴一個成型的式子。所以在工程中如何對一系列測得的值進行關係正確的運算組合是至關重要的。而我認為挺多同學實際上並不明白測算自相關函式的方法，所以大家才會對書第85頁的習題2.12產生不解(周蔭清 隨機過程理論)。他們沒有理解為什麼不同的樣本函式之間不能相乘。，上邊的具體操作式子才更為重要，因為它體現了自相關函式真正想表達的含義。因為自相關函式在實際工程中是被測出來，再擬合成某個數學表示式的，而不像題目中直接告訴一個成型的式子。所以在工程中如何對一系列測得的值進行關係正確的運算組合是至關重要的。而我認為挺多同學實際上並不明白測算自相關函式的方法，所以大家才會對書第85頁的習題2.12產生不解(周蔭清 隨機過程理論)。他們沒有理解為什麼不同的樣本函式之間不能相乘。

這要從隨機過程的研究物件與確定函式的異同說起。我想若是研究某個確定函式

<img src="https://pic4.zhimg.com/886c6d6477f90ccc584794d9dfc4fd23_b.png" data-rawwidth="34" data-rawheight="23" class="content_image" width="34">的特徵，大家肯定不會覺得研究過程會和的特徵，大家肯定不會覺得研究過程會和<img src="https://pic1.zhimg.com/5e0c7ce74fe4b597d35100e4a0f092ac_b.png" data-rawwidth="35" data-rawheight="23" class="content_image" width="35">有什麼聯絡。而隨機過程的研究和確定函式的研究相同點就是：雖然隨機過程中每次究竟會發生哪個樣本函式並不確定，但是一旦發生了，則就是這個樣本函式，不會串擾了。那麼對於這個已成事實的樣本函式，研究方法和對確定函式的研究是相同的。而隨機過程與確定函式的不同就在於：這個樣本函式並不是次次都會發生，所以要求統計特徵。但是統計特徵的獲取是在把每個樣本函式當做確定函式處理變換後，再對變換後的一系列新的樣本函式求算數平均（類比X是一個連續的隨機變數，其概率密度函式為f（x），y=g（x），求y的統計特性）。所以求算數平均前的操作都是限制在各個樣本函式內部的，不同樣本函式間不發生關聯。求算數平均前的操作即為與確定函式相同的地方。有什麼聯絡。而隨機過程的研究和確定函式的研究相同點就是：雖然隨機過程中每次究竟會發生哪個樣本函式並不確定，但是一旦發生了，則就是這個樣本函式，不會串擾了。那麼對於這個已成事實的樣本函式，研究方法和對確定函式的研究是相同的。而隨機過程與確定函式的不同就在於：這個樣本函式並不是次次都會發生，所以要求統計特徵。但是統計特徵的獲取是在把每個樣本函式當做確定函式處理變換後，再對變換後的一系列新的樣本函式求算數平均（類比X是一個連續的隨機變數，其概率密度函式為f（x），y=g（x），求y的統計特性）。所以求算數平均前的操作都是限制在各個樣本函式內部的，不同樣本函式間不發生關聯。求算數平均前的操作即為與確定函式相同的地方。

然而既然引入自相關函式的目的是為了描述樣本函式變化的劇烈程度，直觀的想，若讓我來做，我一定會在一個樣本函式上取兩個時刻的函式值，然後 讓它們相減，看差距的大小來判斷樣本函式變化的劇烈程度。為什麼書中會想到相乘呢？這個問題我想了許久，我發現當是兩個隨機變數的均值和方差相同時，似乎變化劇烈的樣本函式的自相關函式是會大一些，但是我無法用嚴格的數學推匯出來，而且關於樣本函式長什麼樣就叫變化平緩，長什麼樣就叫變化劇烈也並沒有定量的定義，所以我推不下去了。這時我突然發現隨機過程題目中從來沒有通過比較兩個隨機過程自相關函式的大小來確定它們哪個樣本函式變化更劇烈。所以或許雖然自相關函式的引入是從描述樣本函式的變化劇烈程度來的，但是自相關函式的真正作用並非如此。

縱觀全書，非常多的統計特性量都是由自相關函式變化而成，所以自相關函式的真正意義是基本元素。

比如在隨機過程的線性變換那章講到了隨機過程的均方積分和微分，可看出研究的物件仍是類似於確定函式的，比如是否連續，是否可導，然後再討論積分微分結果的特性。但由於研究物件並非確定函式，所以引入均方連續放寬條件，即不需要每個樣本函式都連續，而是大部分連續，即便極個別跳變在做統計平均後其影響也被削弱。這時連續就需要對相鄰兩時間函式值的差值求期望。但是為了數學處理的方便，我們不願意每次都分辨差值的正負然後再讓大的減去小的以避免不適當的抵消，我們經常直接對差值求平方後再求期望。在展開平方的過程中式子將變成<img src="https://pic3.zhimg.com/960ab50dee2789bb05abf0332ad48722_b.png" data-rawwidth="322" data-rawheight="24" class="content_image" width="322">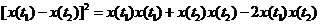

可以看出，展開後的每一項都是自相關函式的形式。

另外的例子有：<img src="https://pic1.zhimg.com/48836e7875877b9224b254f2728a010c_b.png" data-rawwidth="256" data-rawheight="46" class="content_image" width="256">

展開後會出現很多類似x（t1）x（t2）的項

所以用自相關函式作為基本元素的好處就是對於一個隨機過程，只需實際測出一些值算出（擬合出）自相關函式的表示式，之後若想得到這個隨機過程的其他數字特徵都可基於測得的相關函式通過一些變換（如加減，積分，求導）得出，而不用每想求一個統計特徵時都得實際測量一組值了。

而若是用<img src="https://pic2.zhimg.com/059c1376865ad993ebac10d2d3770e1d_b.png" data-rawwidth="88" data-rawheight="23" class="content_image" width="88">來做基本元素，實際操作起來不方便，因為對每一組值都要判斷正負，而且若是需要求隨機變數X（t）的二重積分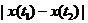，來做基本元素，實際操作起來不方便，因為對每一組值都要判斷正負，而且若是需要求隨機變數X（t）的二重積分，<img src="https://pic2.zhimg.com/059c1376865ad993ebac10d2d3770e1d_b.png" data-rawwidth="88" data-rawheight="23" class="content_image" width="88">也是用不上的。也就是說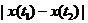也是用不上的。也就是說<img src="https://pic2.zhimg.com/059c1376865ad993ebac10d2d3770e1d_b.png" data-rawwidth="88" data-rawheight="23" class="content_image" width="88">雖然可以描述樣本函式的變化劇烈程度，但是用實驗的方法測得它並不能為以後求其他的數字特徵帶來方便。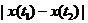而雖然可以描述樣本函式的變化劇烈程度，但是用實驗的方法測得它並不能為以後求其他的數字特徵帶來方便。而<img src="https://pic3.zhimg.com/8eaaa7e395c71dbc7e66ee93b7548f3a_b.png" data-rawwidth="94" data-rawheight="24" class="content_image" width="94">雖然省去了判斷正負的麻煩，但是它同樣不會作為組成其他數字特徵求解表示式的基本項，因此無法被推廣使用。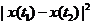雖然省去了判斷正負的麻煩，但是它同樣不會作為組成其他數字特徵求解表示式的基本項，因此無法被推廣使用。

基於上述考慮，我開始思考或許自相關函式的引出順序並不像書中介紹的那樣最初是為了描述樣本函式的變化劇烈程度。而是古人在研究一系列感興趣的數字特徵時發現它們的表示式中有著共同的基本項，因此產生了把這個基本項單獨提出來研究的想法。

這樣的研究思路讓我聯想到了很多學科。線性代數應該是上大學以來第一個明確提出基的思想的科目。它打碎事物千變萬化紛雜的表象，探尋組成表面不同事物的基本分量的特性。基本分量具有無冗餘和完備性的特徵，這使得我們對看似複雜不同的事物的研究大大簡化，也更接近於本質。物理的基是微積分中的微元，形狀不同的物體經過無限分割後變成一堆性質相同的小塊，研究清楚每個小塊的作用特性，再應用線性疊加原理，即可獲得複雜各異的問題的求解。訊號與系統中傅立葉變換也是利用了基的思想，把千變萬化的時域訊號分解成正交完備的三角函式的線性疊加。若系統也是線性時不變的，則系統對時域訊號的作用可看成是分別對每個組成時域訊號的正弦分量作用再將每個正弦分量作用的結果進行線性疊加。這樣一來不用對每個特別的時域訊號進行基於訊號本身特性進行分析，而是隻要研究清楚正弦訊號輸入時的響應即可，由此得到通用的求解方法。

科學研究一個重要的關注點就是如何找到解決問題的通用方法，以省去冗餘的分析和處理，而基本元素的確立為通用性奠定了基礎。