二分類支援向量機模型SVM知識點詳解
1 引言
在本篇部落格中,你將會了解到支援向量機分類器名字的由來、它的基本假設、支援向量機針對線性可分、廣義線性、非線性情況下的解決方法以及一些具體的推導過程,支援向量機常見問題的解答。在本篇部落格的第二部分會給一幅支援向量機整個過程的流程圖,從圖中你可以清晰的瞭解到支援向量機模型針對不同情況的的建立和求解過程,以及他們之間的關係,在圖中涉及到的關鍵細節知識,會在第三部分給出詳細的說明。因此,即使你之前沒有接觸過SVM,在你認真讀了該篇部落格也會有一個清晰的支援向量機建模框架。在本篇部落格的最後將會給出支援向量機SVM從建模到求解整個過程的python實現程式碼及測試結果。廢話不多說,開啟你的學霸模式吧~
2 SVM全流程示意圖
下圖主要展示了,支援向量機構建時原問題,對偶問題及求解過程

2.1 圖說三種分類情況
圖一展示了線性可分情況,如圖所示,圖二展示了存在少量誤分類點的線性可分情況,圖三展示了非線性分類情況。
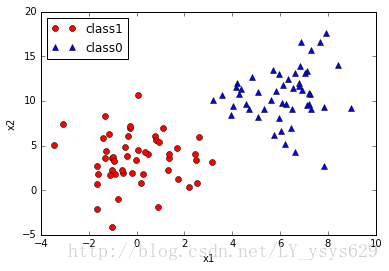
圖1 線性可分情況

圖2 線性不完全可分情況

圖2非線性可分情況
2.2 7條說明詳細解釋SVM的關鍵知識點
- 說明1 –SVM的基本假設:
SVM模型是由少量幾個樣本點決定的,這幾個樣本點稱為支援向量,支援向量距離超平面的距離是小於等於1的(原因後邊有解釋),假如SVM能夠找出一個超平面或者超曲面使得支援向量能夠儘可能的分類正確,且距離超平面或超曲面的距離儘可能的遠,則非支援向量點,也能被正確分類且距離最遠,該處距離的含義可認為分類正確的置信度,距離越遠置信度越大。
說明2 –SVM的模型描述:
SVM模型超平面描述為:
ww∗xx+b=0
決策函式f(x)=sign(ww∗xx+b)
為什麼說策略是間隔最大?接下來會給出答案。
首先提一下兩個概念:函式間隔和幾何間隔(上述假設中的距離)
函式間隔:γ^i=yi(ww∗xi+b)
幾何間隔:γi=γ^||ww||
(想象下點到線的距離,分類正確時,yi(ww∗xi+b)=||ww∗xi+b|| )
假設,分類超平面已經確定,此時要找出距離超平面最短的樣本點(支援向量點),可描述為:
γ=mini=1,2,...,nγi=mini=1,2,...,nγ^||ww||
根據假設,求該距離最大化時的超平面引數w ,描述為:w,b
maxww,bγ 等價於maxww,bγ^||ww||
maxww,bγ^||ww||s.t.yi(ww∗xi+b)≥γ^i=1,2,...,n,(1)
由於γ^ 對求解優化問題無影響,因此可令其為1γ^=1 證明如下:
假設超平面引數為ww∗,b∗ ,支援向量樣本點為(xmin,ymin) ,則支援向量的函式間隔為
γ^=ymin(ww∗xmin+b∗)(2)
由於超平面同時縮放所有引數不會改變,所以令ww∗=w
