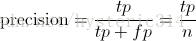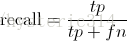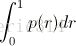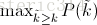召回率（Recall），精確率（Precision），平均正確率（AP），交除並（IoU）

摘要

在訓練YOLO v2的過程中，系統會顯示出一些評價訓練效果的值，如Recall，IoU等等。為了怕以後忘了，現在把自己對這幾種度量方式的理解記錄一下。
這一文章首先假設一個測試集，然後圍繞這一測試集來介紹這幾種度量方式的計算方法。

大雁與飛機

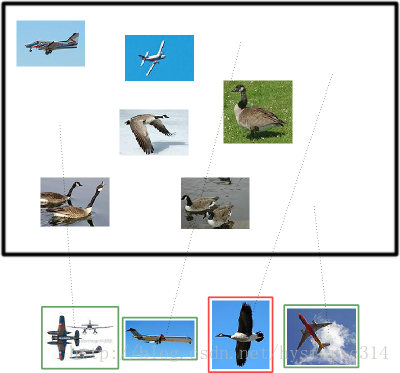
假設現在有這樣一個測試集，測試集中的圖片只由大雁和飛機兩種圖片組成，如下圖所示：

假設你的分類系統最終的目的是：能取出測試集中所有飛機的圖片，而不是大雁的圖片。

現在做如下的定義：
True positives : 飛機的圖片被正確的識別成了飛機。
True negatives:

假設你的分類系統使用了上述假設識別出了四個結果，如下圖所示：

那麼在識別出的這四張照片中：
True positives : 有三個，畫綠色框的飛機。
False positives: 有一個，畫紅色框的大雁。

沒被識別出來的六張圖片中：
True negatives : 有四個，這四個大雁的圖片，系統正確地沒有把它們識別成飛機。
False negatives: 有兩個，兩個飛機沒有被識別出來，系統錯誤地認為它們是大雁。

Precision 與 Recall

Precision其實就是在識別出來的圖片中，True positives所佔的比率：

其中的n代表的是(True positives + False positives)，也就是系統一共識別出來多少照片 。
在這一例子中，True positives為3，False positives為1，所以Precision值是 3/（3+1）=0.75。
意味著在識別出的結果中，飛機的圖片佔75%。

Recall 是被正確識別出來的飛機個數與測試集中所有飛機的個數的比值：

Recall的分母是(True positives + False negatives)，這兩個值的和，可以理解為一共有多少張飛機的照片。
在這一例子中，True positives為3，False negatives為2，那麼Recall值是 3/（3+2）=0.6。
意味著在所有的飛機圖片中，60%的飛機被正確的識別成飛機.。

調整閾值

你也可以通過調整閾值，來選擇讓系統識別出多少圖片，進而改變Precision 或 Recall 的值。
在某種閾值的前提下（藍色虛線），系統識別出了四張圖片，如下圖中所示：

分類系統認為大於閾值（藍色虛線之上）的四個圖片更像飛機。

我們可以通過改變閾值（也可以看作上下移動藍色的虛線），來選擇讓系統識別能出多少個圖片，當然閾值的變化會導致Precision與Recall值發生變化。比如，把藍色虛線放到第一張圖片下面，也就是說讓系統只識別出最上面的那張飛機圖片，那麼Precision的值就是100%，而Recall的值則是20%。如果把藍色虛線放到第二張圖片下面，也就是說讓系統只識別出最上面的前兩張圖片，那麼Precision的值還是100%，而Recall的值則增長到是40%。

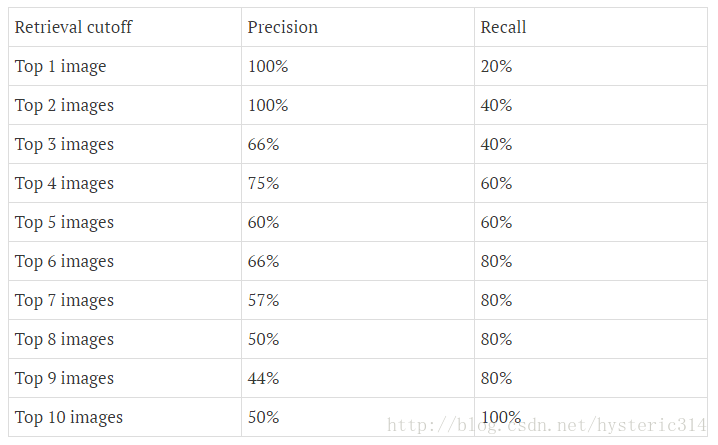
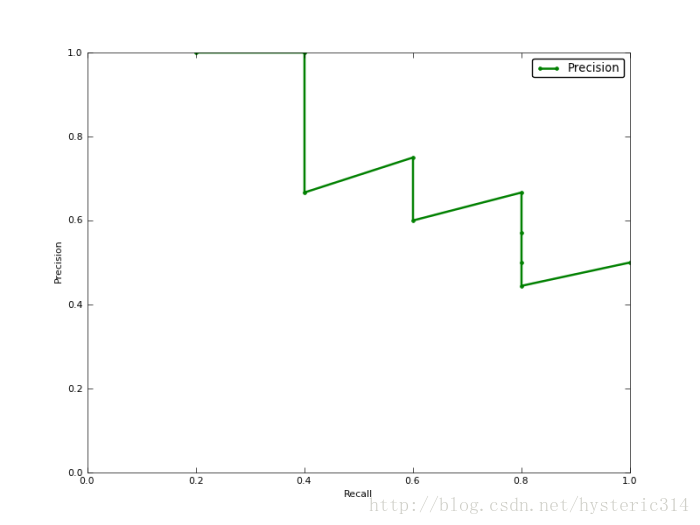
下圖為不同閾值條件下，Precision與Recall的變化情況：

Precision-recall 曲線

如果你想評估一個分類器的效能，一個比較好的方法就是：觀察當閾值變化時，Precision與Recall值的變化情況。如果一個分類器的效能比較好，那麼它應該有如下的表現：被識別出的圖片中飛機所佔的比重比較大，並且在識別出大雁之前，儘可能多地正確識別出飛機，也就是讓Recall值增長的同時保持Precision的值在一個很高的水平。而效能比較差的分類器可能會損失很多Precision值才能換來Recall值的提高。通常情況下，文章中都會使用Precision-recall曲線，來顯示出分類器在Precision與Recall之間的權衡。

上圖就是分類器的Precision-recall 曲線，在不損失精度的條件下它能達到40%Recall。而當Recall達到100%時，Precision 降低到50%。

Approximated Average precision

相比較與曲線圖，在某些時候還是一個具體的數值能更直觀地表現出分類器的效能。通常情況下都是用 Average Precision來作為這一度量標準，它的公式為：

在這一積分中，其中p代表Precision ，r代表Recall，p是一個以r為引數的函式，That is equal to taking the area under the curve.

實際上這一積分極其接近於這一數值：對每一種閾值分別求（Precision值）乘以（Recall值的變化情況），再把所有閾值下求得的乘積值進行累加。公式如下：

在這一公式中，N代表測試集中所有圖片的個數，P(k)表示在能識別出k個圖片的時候Precision的值，而 Delta r(k) 則表示識別圖片個數從k-1變化到k時（通過調整閾值）Recall值的變化情況。

在這一例子中，Approximated Average Precision的值
=(1 * （0.2-0）) + (1 * (0.4-0.2)) + (0.66 * (0.4-0.4)) + (0.75 * (0.6-0.4)) + (0.6 * (0.6-0.6)) + (0.66 * (0.8-0.6)) + (0.57 * (0.8-0.8)) + (0.5 * (0.8-0.8)) + (0.44 * (0.8-0.8)) + (0.5 * (1-0.8)) = 0.782.

=(1 * 0.2) + (1 * 0.2) + (0.66 * 0) + (0.75 * 0.2) + (0.6 *0) + (0.66 * 0.2) + (0.57 *0) + (0.5 *0) + (0.44 *0) + (0.5 * 0.2) = 0.782.

通過計算可以看到，那些Recall值沒有變化的地方（紅色數值），對增加Average Precision值沒有貢獻。

Interpolated average precision

不同於Approximated Average Precision，一些作者選擇另一種度量效能的標準：Interpolated Average Precision。這一新的演算法不再使用P(k)，也就是說，不再使用當系統識別出k個圖片的時候Precision的值與Recall變化值相乘。而是使用：

也就是每次使用在所有閾值的Precision中，最大值的那個Precision值與Recall的變化值相乘。公式如下：

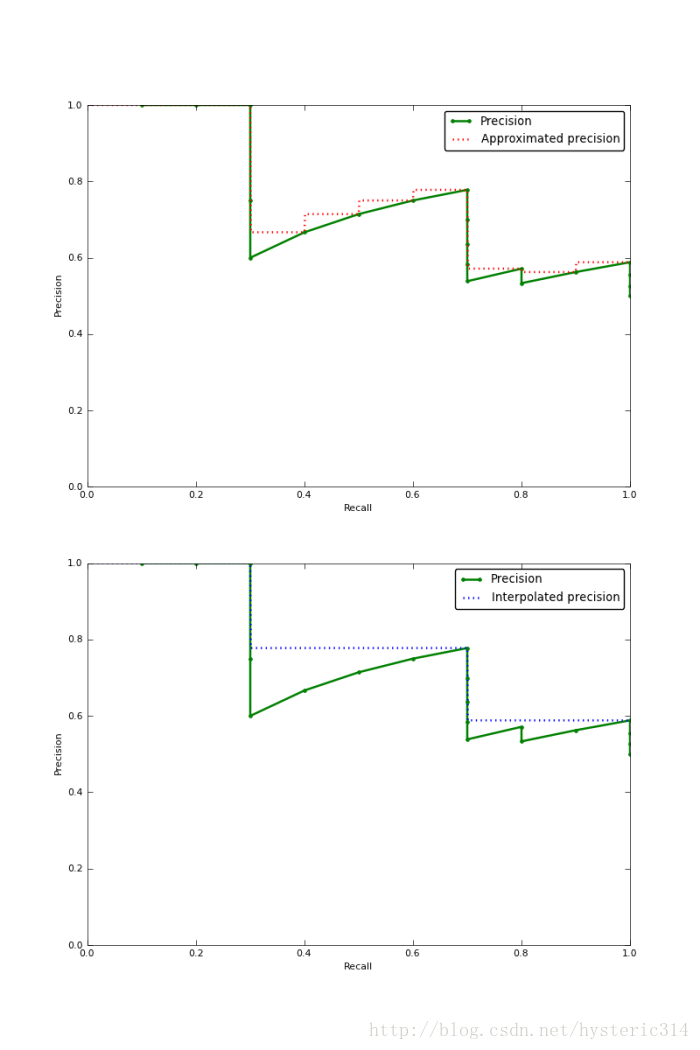
下圖的圖片是Approximated Average Precision 與 Interpolated Average Precision相比較。
需要注意的是，為了讓特徵更明顯，圖片中使用的引數與上面所說的例子無關。

很明顯 Approximated Average Precision與精度曲線挨的很近，而使用Interpolated Average Precision算出的Average Precision值明顯要比Approximated Average Precision的方法算出的要高。

一些很重要的文章都是用Interpolated Average Precision 作為度量方法，並且直接稱算出的值為Average Precision 。PASCAL Visual Objects Challenge從2007年開始就是用這一度量制度，他們認為這一方法能有效地減少Precision-recall 曲線中的抖動。所以在比較文章中Average Precision 值的時候，最好先弄清楚它們使用的是那種度量方式。

IoU

IoU這一值，可以理解為系統預測出來的框與原來圖片中標記的框的重合程度。
計算方法即檢測結果Detection Result與 Ground Truth 的交集比上它們的並集，即為檢測的準確率：

如下圖所示：
藍色的框是：GroundTruth
黃色的框是：DetectionResult
綠色的框是：DetectionResult ⋂GroundTruth
紅色的框是：DetectionResult ⋃GroundTruth