一隻小蜜蜂...

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 36202    Accepted Submission(s): 13302

Problem Description 有一隻經過訓練的蜜蜂只能爬向右側相鄰的蜂房，不能反向爬行。請程式設計計算蜜蜂從蜂房a爬到蜂房b的可能路線數。
其中，蜂房的結構如下所示。


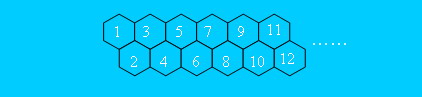
Input 輸入資料的第一行是一個整數N,表示測試例項的個數，然後是N 行資料，每行包含兩個整數a和b(0<a<b<50)。

Output 對於每個測試例項，請輸出蜜蜂從蜂房a爬到蜂房b的可能路線數，每個例項的輸出佔一行。

Sample Input 2 1 2 3 6
Sample Output 1 3 分析：

1、“蜜蜂只能爬向右側相鄰的蜂房”準確來說，包含三個方向：正右方，右下方，右上方。

2、到 1 只有一條路（本身嘛），到 2 有一條路線（1 —> 2），到 3 有兩條路線（1 —>3 或者 2 —> 3），到 4 有 3 條路線（到 2 的 1 條加上到 3 的 2 條），到 5 有 5  條路線（到 3 的 2 條加上到 4 的 3 條）……

3、以此類推，從原點到達各個蜂房的路線數分別為：

蜂房號	1	2	3	4	5	6	7	8	9	……
路線數	1	1	2	3	5	8	13	21	34	……

不難看出，這是一個斐波那契數列！只要能看出這個關鍵點，AC這道題就很容易了。

import java.util.Scanner;

public class Main {

	static long[] count = new long[50];

	static {
		count[0] = count[1] = 1;
		for (int i = 2; i < 50; i++) {
			count[i] = count[i - 1] + count[i - 2];
		}
	}

	public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		int n = scanner.nextInt();

		while (n-- != 0) {
			int a = scanner.nextInt();
			int b = scanner.nextInt();
			int num = b - a;

			System.out.println(count[num]);
		}
	}
}