據文章說，原文是俄文的，各種翻譯才成為中文。表示膜拜，仰慕。ORZ。就需要這麼屌屌噠人。。

容斥原理的具體證明就不在描述了。。

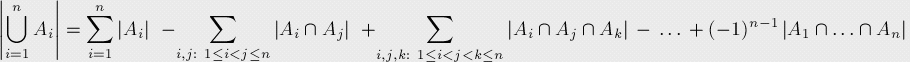
這應該是對容斥原理最簡單粗暴的解釋了。。

我們這篇文章關鍵解釋了幾個有關容斥原理的小小問題。

1.一個簡單的排列問題。

由0到9的數字組成排列，要求第一個數大於1，最後一個小於8，問，共有多少種排列？

分析：直接求的話，求起來很複雜。那麼我們可以求該排列的逆問題。也就是求第一數<=1，或者最後一位數>=8的排列數。

我們假設A為第一個數<=1，B為最後一個數>=8。

那麼我們要求的逆問題的排列數就是A + B - (A & B)。(我們定義‘+’為集合的並，&為集合的交集，數學符號和邏輯符號並用，望諒解)。。

為什麼藥減去A & B呢？因為我們的A，也就是說第一個數<=1中也有滿足最後一個數>=8的情況，同樣的最後一個數>=8的情況中也有第一個數<=1的，那麼我們A+B就會多加一部分第一個數<=1&&最後一個數>=8，減去的就是這一部分。。

C = A + B - (A & B) = 2 * 9! + 2 * 9! - 2 * 2 * 8!。那麼這部分就是第一位<=1，或者最後一個>=8的排列數。。

我們用10! - C就是我們要求的，第一個數大於1，最後一個數小於8的排列數。。

2.(0, 1, 2)序列問題。

長度為n，由0，2，1組成序列，每個數最少出現一次，這樣的序列有多少種。

分析：我們發現，直接求解的話也是比較複雜的。。那麼我們就可以求解他是逆問題。

也就是不全部出現0，1，2的序列會有多少種。。用原文是話就是，不出現某些數的序列的種數。

我們設A0是不出現0的序列的個數，A1是不出現1的序列的個數，A2是不出現2的序列的個數。

A0 + A1 + A2 - (A0 & A1) - (A0 & A2) - (A1 & A2) + (A0 & A1 & A2)。就是我們所要求的逆問題是序列。看下面的維恩圖：

畫的有點挫（不是有點，是太挫了。。。。 - -）。。

可以看來我們可以用另一個問題來解釋了。。這個問題是維恩圖與求同時不能被三個數整除的一樣了。。其實差不多。。

C = A0 + A1 + A2 - (A0 & A1) - (A0 & A2) - (A1 & A2) + (A0 & A1 & A2) = 2^n + 2^n + 2^n - 1 - 1 - 1 + 0.。這就是序列中不出現某些數序列的種類數。。。

總共是序列眾數 3^n - (3 * 2^n - 3 + 0)。。就是我們所求的每個數都最少出現一次的序列數。。

3.方程整數解問題。

給一個方程 x1 + x2 + x3 + x4 + x5 + x6 = 20， 0 <= xi <= 8。。問這樣的整數解有多少種。。

4.求指定區間內與n互素的數有多少個。。

給定r，n 求[1，r]內與n互素的個數有多少個？看到這個問題，數論有學一點的童鞋可能會想如果r = n的話，不就是尤拉函數了嗎？是的，可惜這個問題的r ，n是不一定會相等的。。

分析：直接求解問題就是比較複雜的。所以我們還是研究這個問題是逆問題。也就是說求gcd(k，n) >= 2，在1 -  n 之間k有多少個 。

那麼我們就可以列舉n的素因子來進行求解。。。

Code：小小程式碼：

//時間複雜度O(sqrt(n))...
int solve(int r, int n)
{
    int p[N], top = 0, ans;
    for(int i = 2; i * i <= n; i ++){
        if(n % i == 0){
            p[top ++] = i;
            while(n % i == 0) n = n / i;
        }
    }
    if(n > 1) p[top ++] = n;
    //列舉子集來進行判斷加減,cnt為子集元素個數
    for(int i = 1; i < (i << top); i ++){
        int cnt = 0, tmp = 1;
        for(int j = 0; j < top; j ++){
            cnt ++;
            tmp = tmp * p[j];
        }
    }
    if(cnt % 2) ans += r / tmp;
    else ans -= r / tmp;
    return r - ans;
}

5.在給定區間內被給定集合中至少一個數整除的個數。。

6.能滿足一定數目匹配的字串個數問題。

7.路徑數目問題。

8.素數四元組問題。

給你n個數