在推薦中，關聯規則推薦使用的比較頻繁，畢竟是通過概率來預測的，易於理解且準確度比較高，不過有一個缺點為，想要覆蓋推薦物品的數量，就要降低支援度與置信度。過高的支援度與置信度會導致物品覆蓋不過，這裡需要其他的推薦方法合作，建議使用基於Spark的模型推薦演算法（矩陣分解+ALS）.

一FPGrowth演算法描述：

FPGrowth演算法

概念：支援度，置信度，提升度(Spark好像沒有計算這個的函式，需要自己計算)
列子：假如10000個消費者購買了商品，尿布1000個，啤酒2000個，麵包500個，同時購買了尿布和啤酒800個，同時購買了尿布和麵包100個。
1)支援度：在所有項集中出現的可能性，項集同時含有，x與y的概率。是第一道門檻，衡量量是多少，可以理解為‘出鏡率’，一般會支援初始值過濾掉低的規則。
尿布和啤酒的支援度為：800/10000=8%
2)置信度：在X發生的條件下，Y發生的概率。這是第二道門檻，衡量的是質量，設定最小的置信度篩選可靠的規則。
尿布-》啤酒的置信度為:800/1000=80%，啤酒-》尿布的置信度為：800/2000=40%
3)提升度：在含有x條件下同時含有Y的可能性（x->y的置信度）比沒有x這個條件下含有Y的可能性之比：confidence(尿布=> 啤酒)/概率(啤酒)) = 80%/((2000+800)/10000) 。如果提升度=1，那就是沒啥關係這兩個。
通過支援度和置信度可以得出強關聯關係，通過提升的，可判別有效的強關聯關係。

2 FPGrowth特點

1）產生候選集，2）只需要兩次遍歷資料庫，提高效率。
再舉個我們這裡的列子，列如時間的原因是，使用最近的行為訓練規則，太久的行為沒有意義
樣本如下：
列子：使用者，時間，消費的漫畫
u1,20160925,成都1995,seven,神獸退散。
u2,20160925,成都1995,seven,six。
u1,20160922，成都1995，惡魔日記

比如產生了如下規則：
規則：成都1995，seven->神獸退散
這條規則：
成都1995，seven的支援度2/3
成都1995，seven-》神獸退散，的置信度1/2
這裡打個廣告哈，成都1995,seven,神獸退散（漫畫）比較真的比較好看，成都1995也要拍網劇了哈！！

二Spark程式碼實現（修改了一下Spark的列子）

//資料樣本：
r z h k p
z y x w v u t s
s x o n r
x z y m t s q e
z
x z y r q t p
 

package org.wq.scala.ml

import org.apache.spark.mllib.fpm.FPGrowth
import org.apache.spark.{SparkConf, SparkContext}

/**
  * Created by Administrator on 2016/10/24.
  */
object FP_GrowthTest {

  def main(args:Array[String]){
    val conf = new SparkConf().setAppName("FPGrowthTest").setMaster("local").set("spark.sql.warehouse.dir","E:/ideaWorkspace/ScalaSparkMl/spark-warehouse")
    val sc = new SparkContext(conf)
    //設定引數
    //最小支援度
    val minSupport=0.2
    //最小置信度
    val minConfidence=0.8
    //資料分割槽
    val numPartitions=2

    //取出資料
    val data = sc.textFile("data/mllib/sample_fpgrowth.txt")

    //把資料通過空格分割
    val transactions=data.map(x=>x.split(" "))
    transactions.cache()
    //建立一個FPGrowth的演算法實列
    val fpg = new FPGrowth()
    //設定訓練時候的最小支援度和資料分割槽
    fpg.setMinSupport(minSupport)
    fpg.setNumPartitions(numPartitions)

    //把資料帶入演算法中
    val model = fpg.run(transactions)

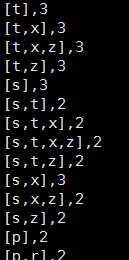
    //檢視所有的頻繁項集，並且列出它出現的次數
    model.freqItemsets.collect().foreach(itemset=>{
     println( itemset.items.mkString("[", ",", "]")+","+itemset.freq)
    })

    //通過置信度篩選出推薦規則則
    //antecedent表示前項
    //consequent表示後項
    //confidence表示規則的置信度
    //這裡可以把規則寫入到Mysql資料庫中，以後使用來做推薦
    //如果規則過多就把規則寫入redis，這裡就可以直接從記憶體中讀取了，我選擇的方式是寫入Mysql，然後再把推薦清單寫入redis
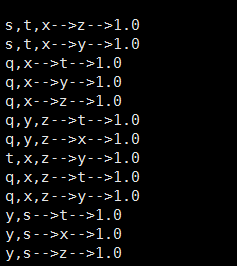
    model.generateAssociationRules(minConfidence).collect().foreach(rule=>{
       println(rule.antecedent.mkString(",")+"-->"+
        rule.consequent.mkString(",")+"-->"+ rule.confidence)
    })
    //檢視規則生成的數量
    println(model.generateAssociationRules(minConfidence).collect().length)

    //並且所有的規則產生的推薦，後項只有1個，相同的前項產生不同的推薦結果是不同的行
    //不同的規則可能會產生同一個推薦結果，所以樣本資料過規則的時候需要去重

  }
}

上面規則是本地執行的，部署的話需要改下哈，程式碼如下

package org.wq.scala.ml

import org.apache.spark.mllib.fpm.FPGrowth
import org.apache.spark.{SparkConf, SparkContext}

/**
  * Created by Administrator on 2016/10/24.
  */
object FP_Growth {

  def main(args:Array[String]){

    if(args.length!=4){
      println("請輸入4個引數 購物籃資料路徑 最小支援度 最小置信度 資料分割槽")
      System.exit(0)
    }

    val conf = new SparkConf().setAppName("FPGrowthTest")
    val sc = new SparkContext(conf)

    val data_path=args(0)
    //設定引數
    //最小支援度
    val minSupport=args(1).toDouble
    //最小置信度
    val minConfidence=args(2).toDouble
    //資料分割槽
    val numPartitions=args(3).toInt


    //取出資料
    val data = sc.textFile(data_path)
    //把資料通過空格分割
    val transactions=data.map(x=>x.split(" "))
    transactions.cache()

    //建立一個FPGrowth的演算法實列
    val fpg = new FPGrowth()
    //設定訓練時候的最小支援度和資料分割槽
    fpg.setMinSupport(minSupport)
    fpg.setNumPartitions(numPartitions)

    //把資料帶入演算法中
    val model = fpg.run(transactions)

    //檢視所有的頻繁項集，並且列出它出現的次數
    model.freqItemsets.collect().foreach(itemset=>{
     println( itemset.items.mkString("[", ",", "]")+","+itemset.freq)
    })

    //通過置信度篩選出推薦規則則
    //antecedent表示前項
    //consequent表示後項
    //confidence表示規則的置信度
    //這裡可以把規則寫入到Mysql資料庫中，以後使用來做推薦
    //如果規則過多就把規則寫入redis，這裡就可以直接從記憶體中讀取了，我選擇的方式是寫入Mysql，然後再把推薦清單寫入redis
    model.generateAssociationRules(minConfidence).collect().foreach(rule=>{
       println(rule.antecedent.mkString(",")+"-->"+
        rule.consequent.mkString(",")+"-->"+ rule.confidence)
    })
    //檢視規則生成的數量
    println(model.generateAssociationRules(minConfidence).collect().length)

    //並且所有的規則產生的推薦，後項只有1個，相同的前項產生不同的推薦結果是不同的行
    //不同的規則可能會產生同一個推薦結果，所以樣本資料過規則的時候需要去重

  }
}

三提交部署

上傳jar與資料到主節點

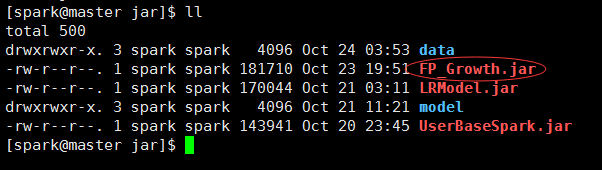
#然後把資料檔案scp到各個節點
cd /home/jar/data
scp sample_fpgrowth.txt spark@slave1:/home/jar/data/
scp sample_fpgrowth.txt spark@slave2:/home/jar/data/

然後提交給spark叢集執行
資料目錄：/home/jar/data
jar目錄：/home/jar
模型目錄：/home/jar/model

spark-submit  --class org.wq.scala.ml.FP_Growth --master spark://master:7077 --executor-memory 700m --num-executors 1  /home/jar/FP_Growth.jar  /home/jar/data/sample_fpgrowth.txt 0.2 0.8 2

執行結果：
頻繁項集：

規則：

叢集跑job資訊

四：注意事項

1我使用了20w多樣本計算，近2000個物品，支援度5%，置信70%，訓練出來的規則很多，最後匹配的規則比較慢，而且物品的覆蓋比較少。所以把近2000的物品修改為主推的近500，這樣規則就減少了很多，切覆蓋的物品也比較多。具體引數自己試下哈，樣本和樣本的結構不一樣。
2FpGrowth的訓練其實比較快的，把樣本量提升到了50w，訓練的時間也是分鐘級別的，10分鐘左右吧，前提是支援度比高。在調整演算法的時間，支援度很重要，關係到執行的時間，我把支援度調整的很低的時候，演算法跑不出來，也會記憶體溢位（本身記憶體也不大哈）。不過時間多也無所謂，因為本身就是離線模型訓練哈。
3引數調整方案，多試試，覺得準確性和物品覆蓋比較滿意的時候就行了額，至於引數的自動迭代，完全沒什麼思路，除了輸入不同引數，求最好。
4訓練的時候資料能cache就cache哈，會比叫快哈
5 這個訓練中，6個樣本，都產生了85個規則，可以想象，樣本量大了之後，規則暴多，所以把規則寫入mysql，group by，group_concat()（會mysql的應該明白我說啥）可以合併規則，把置信度高的放在前面，當然自己寫程式碼可以哈。
s,t,x–>z–>1
s,t,x–>y–>1
合併為s,t,x–>z,y置信度高的在前面哈