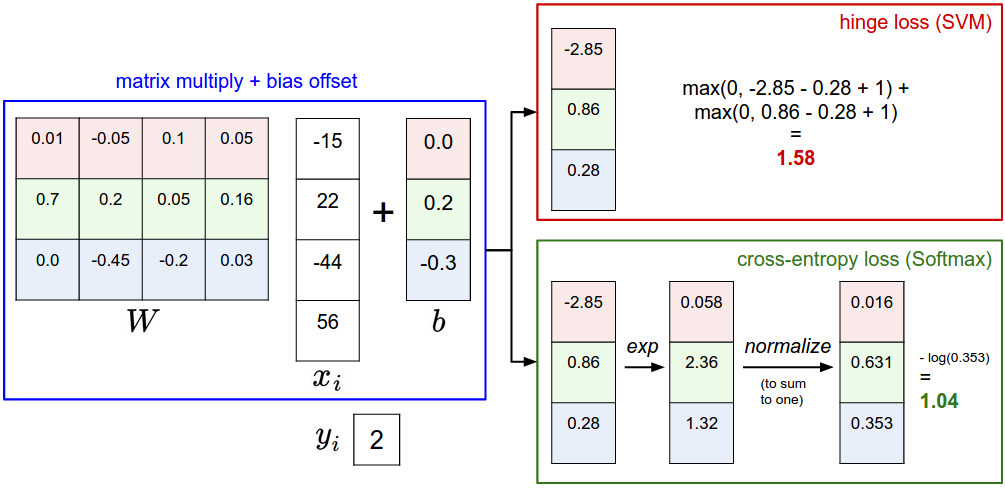
svm損失和交叉熵損失
多分類svm損失
損失函式:
解釋:
SVM想要正確分類的分數
舉例來說:假設通過分類我們得到一個分數向量,s=[13,−7,11],正確的分類是第一個,
第二個分類的損失是0,因為[-7 - 13 + 10]=-10<0,正確的分類13得分比不正確的分類得分-7要高20,大於10,因此損失是0.
第三個分類的損失是8,因為[11 - 13 + 10]=8>0,正確的分類13得分比不正確的分類得分11要高2,小於10,因此損失是8.
也就是說,SVM想要正確分類的分數

Multiclass SVM 想要正確分類的分數
正則化
這種損失函式有一個bug。假設我們有了一個W,可以使得損失是0,但是任何
防止過擬合
交叉熵損失
交叉熵損失通常適用於Softmax 分類器。損失函式:
舉例,和上一個例子一樣通過分類器得到分數向量s=[13,−7,11],正確的分類是第一個。首先將得分取指數,然後歸一化,假如得到[0.3,0.1,0.6],則損失是
交叉熵函式是衡量真實分佈p與假設分佈q之間的不一致性:
真實分佈p=[0,…1,…,0],假設分佈
實戰技巧:
因為
通常
程式碼:
f = np.array([123, 456, 789]) # example with 3 classes and each having large scores
p = np.exp(f) / np.sum(np.exp(f)) # Bad: Numeric problem, potential blowup
# instead: first shift the values of f so that the highest number is 0:
f -= np.max(f) # f becomes [-666, -333, 0]
p = np.exp(f) / np.sum(np.exp(f)) # safe to do, gives the correct answer比較
SVM和Softmax之間的效能差異通常很小,不同的人對於哪個分類器工作得更好會有不同的意見。與Softmax分類器相比,SVM是一個更區域性的目標,可以被認為是一個錯誤或一個特徵。考慮一個實現分數[10,-2,3]和第一類是正確的例子。 SVM(例如,具有期望的餘量Δ=1)將看到,與其他類相比,正確的類已經具有高於餘量的分數,並且它將計算零損失。 SVM不關心個別分數的細節:如果它們改為[10,-100,-100]或[10,9,9],則SVM將是無關的,因為滿足1的餘量,因此損失是零。然而,這些情況不等同於Softmax分類器,它將為分數[10,9,9]比[10,-100,-100]積累更高的損失。換句話說,Softmax分類器從不完全滿意它產生的分數:正確的類可以總是具有較高的概率,並且不正確的類總是較低的概率,並且損失將總是變得更好。然而,一旦滿足邊緣,SVM就ok了,並且它不會精確地超越該約束的精確得分。這可以直觀地被認為是一個特徵:例如,可能花費大部分“努力”在將車輛與卡車分離的困難問題上的汽車分類器不應該受到青蛙例子的影響,其已經指定非常低分數到,並且可能聚集在資料的完全不同側。
