Java 排序演算法-歸併排序
演算法思想
歸併排序(MergeSort)是將兩個(或兩個以上)有序表合併成一個新的有序表,即把待排序序列分為若干個子序列,每個子序列是有序的。然後再把有序子序列合併為整體有序序列。
歸併排序是建立在歸併操作上的一種有效的排序演算法。該演算法是採用分治法(Divide and Conquer)的一個非常典型的應用。 將已有序的子序列合併,得到完全有序的序列;即先使每個子序列有序,再使子序列段間有序。若將兩個有序表合併成一個有序表,稱為2-路歸併。
演算法原理
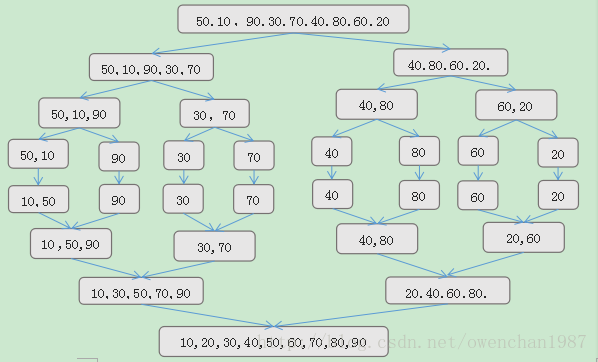
歸併演算法的示意圖(圖片來自維基百科)
演算法實現
使用遞迴的歸併排序
public class TestJava {
private 歸併排序的優化(非遞迴歸併排序)
public class CustomMergeSort {
private static int[] array = new int[]{11, 4, 5, 6, 1, 2, 16, 3, 44, 21, 22, 8, 9, 7, 2, 6};
public static void main(String[] args) {
mergeSort();
for (int i : array) {
System.out.println(i);
}
}
public static void mergeSort() {
int len = array.length;
int k = 1;
while (k < len) {
mergePass(array, k, len);
k *= 2;
}
}
private static void mergePass(int[] array, int k, int n) {
int i = 0;
while (i < n - 2 * k + 1) {
merge(array, i , i + 2 * k - 1);
i += 2* k;
}
if (i < n - k) {
merge(array, i, n -1);
}
}
private static void merge(int[] array, int left, int right) {
if (left >= right) {
return;
}
int middle = (left + right) / 2;
int[] A = new int[middle - left + 1];
int[] B = new int[right - middle];
System.arraycopy(array, left, A, 0, A.length);
System.arraycopy(array, middle + 1, B, 0, B.length);
int i = 0;
int j = 0;
for (int index = left; index <= right; index++) {
if (i < A.length && j < B.length) {
array[index] = A[i] < B[j] ? A[i ++] : B[j ++];
} else if (i < A.length) {
array[index] = A[i ++];
} else if (j < B.length) {
array[index] = B[j ++];
}
}
}
}演算法分析
(1)穩定性
歸併排序是一種穩定的排序。
(2)儲存結構要求
可用順序儲存結構。也易於在連結串列上實現。
(3)時間複雜度
對長度為n的檔案,需進行 趟二路歸併,每趟歸併的時間為O(n),故其時間複雜度無論是在最好情況下還是在最壞情況下均是O(nlgn)。
(4)空間複雜度
需要一個輔助向量來暫存兩有序子檔案歸併的結果,故其輔助空間複雜度為O(n),顯然它不是就地排序。
相關推薦
[排序演算法]--歸併排序的Java實現
歸併排序(2-路歸併):歸併排序是建立在歸併操作上的一種有效的排序演算法。該演算法是採用分治法(Divide and Conquer)的一個非常典型的應用,歸併排序將兩個已排序的表合併成一個表。 下面先看一個歸併排序過程的示例: 待排序列(14,12
Java 排序演算法-歸併排序
演算法思想 歸併排序(MergeSort)是將兩個(或兩個以上)有序表合併成一個新的有序表,即把待排序序列分為若干個子序列,每個子序列是有序的。然後再把有序子序列合併為整體有序序列。 歸併排序是建立在歸併操作上的一種有效的排序演算法。該演算法是採用分治法(D
排序演算法—歸併排序的Java實現,效率比選擇排序要低?
初級Java開發人員面試,經常會碰到技術面試官問排序演算法,幾乎每次面試一遍都要刷一遍排序演算法……,今天正在刷歸併排序,居然發現在100000級別的資料量中歸併演算法的執行時間居然比選擇排序要長,百思不得解,最後在比較多位大神blog中的程式碼實現,發現問題的
知識點11:常見的排序演算法–歸併排序
相信看過常見的排序演算法——快速排序的朋友們都記得,我們在介紹它的時候便闡述了使用快排的兩種策略,分別是分治和遞迴。它的原理是:通過遞迴的方式,利用某個基底,不斷將數列劃分為更小的部分。直到小陣列不能再拆分的時候,便已經完成了排序。而今天要介紹的歸併排序,與它有很多相近的地方,不過也有很
排序演算法之歸併排序(關鍵詞:資料結構/演算法/排序演算法/歸併排序)
假定:有 1 個亂序的數列 nums ,其中有 n 個數。 要求:排好序之後是 從小到大 的順序。 歸併排序演算法 程式碼 def merge(a, b): res = [] A = 0 B = 0 while A<len(a) and B<len(b
C++排序演算法——歸併排序
歸併排序C++ 歸併排序從小到大排序:首先讓陣列中的每一個數單獨成為長度為1的區間, 然後兩兩一組有序合併,得到長度為2的有序區間,依次進行,直到合成整個區間。 #include <iostream> using namespace std; /
高階排序演算法-歸併排序
輔助工具 歸併排序 O(nlogn)級別演算法 需要額外的輔助空間 穩定的排序演算法 對於排序演算法穩定性的定義, 這裡直接引用百度詞條: 假定在待排序的記錄序列中,存在多個具有相同的關鍵字的記錄,若經過排序,這些記錄的相對次序保持不變,即在原序列中,r
PHP實現排序演算法----歸併排序(Merging Sort)
基本思想: 歸併排序:就是利用歸併(合併)的思想實現的排序方法。它的原理是假設初始序列含有 n 個元素,則可以看成是 n 個有序的子序列,每個子序列的長度為 1,然後兩兩歸併,得到 ⌈ n / 2⌉ (⌈ x ⌉ 表示不小於 x 的最小整數)個長度為 2 或
【演算法】排序演算法——歸併排序
前言 歸併排序是分治法在排序問題上的運用,因此為了更好地瞭解歸併排序,首先了解一下分治法。分治法的基本思想是:將原問題分解為幾個規模較小但是類似於原問題的子問題,遞迴地求解這些子問題,然後合併子問題的解來建立原問題的解。 分治模式在每層遞
排序演算法---歸併排序
歸併排序的實現分為遞迴實現與非遞迴(迭代)實現。遞迴實現的歸併排序是演算法設計中分治策略的典型應用,我們將一個大問題分割成小問題分別解決,然後用所有小問題的答案來解決整個大問題。非遞迴(迭代)實現的歸併排序首先進行是兩兩歸併,然後四四歸併,然後是八八歸併,一直
【圖解演算法】排序演算法——歸併排序
0.什麼是歸併排序(Merge sort)? 是建立在歸併操作上的一種有效的排序演算法,效率為O(n log n)。1945年由約翰·馮·諾伊曼首次提出。該演算法是採用分治法(Divide and Conquer)的一個非常典型的應用,且各層分治遞迴可以同時進
排序演算法——歸併排序
什麼是歸併排序? 歸併排序簡單來講,就是將兩個有序的序列整合到一起。 如何將兩個有序的序列整合到一起呢? 那麼我們假設,現在有 M={m1 ,m2,m3,....,mx}序列和 N = {n1,n2,n3,....,ny}序列,這兩個序列已經是有序的序列,首先建立一個空序列 K = {},那麼接著將
連結串列排序演算法java實現(連結串列的快速排序、插入排序、歸併排序)
難易程度:★★ 重要性:★★★ 連結串列的排序相對陣列的排序更為複雜些,也是考察求職者是否真正理解了排序演算法(而不是“死記硬背”) 連結串列的插入排序 public class LinkedInsertSort { static cla
排序演算法(Java隨筆)—歸併排序
歸併排序(Merge Sort):將多個有序資料表合併為一個有序資料表,如果被合併的資料表只有兩個,則叫二路歸併。 二路歸併排序的原理步驟: 將長度為n的原資料表分割為n個長度為1的子表,兩兩合併得
3. 排序通常有多種演算法,如氣泡排序、插入排序、選擇排序、希爾排序、歸併排序、快速排序,請選擇任意2種用java實現 [分值:20] 您的回答:(空) (簡答題需要人工評分)
3. 排序通常有多種演算法,如氣泡排序、插入排序、選擇排序、希爾排序、歸併排序、快速排序,請選擇任意2種用java實現 [分值:20] 您的回答:(空) (簡答題需要人工評分) package com.interview; /** * 各種排序演算法 */
Java排序演算法分析與實現:快排、氣泡排序、選擇排序、插入排序、歸併排序(一)
轉載 https://www.cnblogs.com/bjh1117/p/8335628.html 一、概述: 本文給出常見的幾種排序演算法的原理以及java實現,包括常見的簡單排序和高階排序演算法,以及其他常用的演算法知識。 簡單排序:氣泡排序、選擇排序、
五十道程式設計小題目 --- 28 八大排序演算法 java 之 07歸併排序
7. 歸併排序(Merge Sort) 基本思想: 歸併(Merge)排序法是將兩個(或兩個以上)有序表合併成一個新的有序表,即把待排序序列分為若干個子序列,每個子序列是有序的。然後再把有序子序列合併為整體有序序列。 歸併排序示例: 合併方法: 設r[
Java-時間複雜度為O(nlogn)的排序演算法(快速排序, 歸併排序, 堆排序, 希爾排序)
/** 包含多種靜態排序方法 * Created by Andre on 2016/6/27. */ public class Sorter { /** * 快速排序 * 遞迴形式 * 第一個記錄為樞軸 * 不穩定
java排序演算法—氣泡排序
快速排序 氣泡排序的思想方法: 1.從無序序列頭部開始,進行兩兩比較,根據大小交換位置,直到最後將最大(小)的資料元素交換到了無序佇列的隊尾,從而成為有序序列的一部分; 2.下一次繼續這個過程,直到所有資料元素都排好序。演算法的核心在於每次通過兩兩比較交換位置,選出剩餘無序序列裡最大(小
java排序演算法—快速排序
快速排序 快速排序的思想方法: 1.先從數列中取出一個數作為基準數,記為x。 2.分割槽過程,將不小於x的數全放到它的右邊,不大於x的數全放到它的左邊。(這樣key的位置左邊的沒有大於key的,右邊的沒有小於key的,只需對左右區間排序即可)。 3.再對左右區間重複第二步,直到各區間