歸併排序（2-路歸併）：歸併排序是建立在歸併操作上的一種有效的排序演算法。該演算法是採用分治法（Divide and Conquer）的一個非常典型的應用，歸併排序將兩個已排序的表合併成一個表。

下面先看一個歸併排序過程的示例：
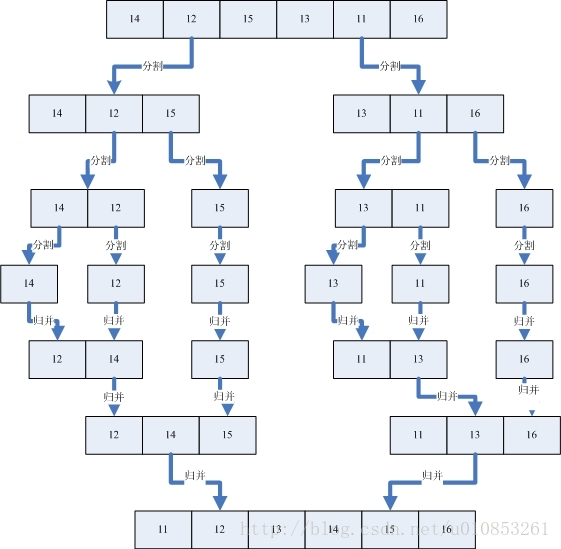
待排序列（14,12,15,13,11,16）：
首先用分割的方法，將這個序列分割成一個個已經排好序的子序列，然後再利用歸併的辦法將一個個子序列合併成排好序的序列，如下圖：

上面很明顯就是採用先 “分割” 再 “合併” 的思想。我們首先把一個未排序的序列從中間分割成2部分，再把2部分分成4部分，依次分割下去，直到分割成一個一個的資料，再把這些資料兩兩歸併到一起，使之有序，不停的歸併，最後成為一個排好序的序列。

下面首先考慮怎麼把兩個有序的序列合併。這個非常簡單，只要從比較二個數列的第一個數，誰小就先取誰，取了後就在對應數列中刪除這個數。然後再進行比較，如果有數列為空，那直接將另一個數列的資料依次取出即可。原始碼如下：

/**
 * 把有序陣列a和有序陣列b 合併到陣列c中，這裡假設陣列c的容量足夠大，可以容納陣列a和陣列b中的所有元素。
 * @param a
 * @param n 陣列a的長度n
 * @param b
 * @param m 陣列b的長度m
 * @param c
 */
public static void mergeArray(int a[], int n, int b[], int
 
 m, int c[]){
    int i,j,k;
    //索引
    i=j=k=0;

    while (i < n && j < m){
        if(a[i] < b[j]){
            c[k++] = a[i++];
        } else {
            c[k++] = b[j++];
        }
    }
    //將陣列a或則b中剩餘的元素加入陣列c中
    while (i<n){
        c[k++] = a[i++];
    }

    while (j < m){
        c[k++] = b[j++];
    }
}//end
 

上面的合併演算法的效率還是比較高的，可以達到O(n)的時間複雜度。

上面已經解決了合併有序序列的問題，下面再來看看二路歸併的方法，其的基本思路就是將陣列分成二組A，B，如果這二組組內的資料都是有序的，那麼就可以很方便的將這二組資料進行排序。如何讓這二組組內資料有序了？

可以將A，B組各自再分成二組。依次類推，當分出來的小組只有一個數據時，可以認為這個小組組內已經達到了有序，然後 再合併相鄰的二個小組就可以了。這樣通過先遞迴的分解數列，再合併數列就完成了歸併排序。 原始碼如下：

/**
 * 將a[first, mid] 和 a[mid+1, last] 合併
 * @param a
 * @param first
 * @param mid
 * @param last
 * @param temp
 */
private static void mergeArray(int a[], int first, int mid, int last, int temp[]){
    int i = first, j=mid+1;//設定兩個陣列的起始邊界
    int m=mid, n=last;//設定兩個陣列的結束邊界

    int k=0;

    while (i <= m && j<=n){
        if(a[i] <= a[j]){
            temp[k++] = a[i++];
        }else {
            temp[k++] = a[j++];
        }
    }

    while (i<=m){
        temp[k++] = a[i++];
    }

    while (j <= n){
        temp[k++] = a[j++];
    }

    for(i=0; i<k; i++){
        a[first+i] = temp[i];
    }
}

/**
 * 二路歸併  使用遞迴解決.
 * @param a
 * @param first 陣列的起始下標
 * @param last 陣列的結束下標
 * @param temp 輔助陣列
 */
public static void mergeSort(int[] a, int first, int last, int[] temp){
    if(first < last) {
        int mid = (first + last)/2;

        mergeSort(a, first, mid, temp);//左邊有序
        mergeSort(a, mid+1, last, temp);//右邊有序

        mergeArray(a, first, mid, last, temp); //再將兩個有序序列合併.
    }
}

測試：

public static void main(String[] args) {
    int[] arr = {1,9,3,12,7,8,3,4,65,22};
    int[] temp = {0,0,0,0,0,0,0,0,0,0};


    mergeSort(arr, 0, arr.length-1, temp);

    for(int i:arr){
        System.out.print(i+",");
    }
}

輸出：

1,3,3,4,7,8,9,12,22,65,

歸併排序的效率是比較高的，設數列長為N，將數列分開成小數列一共要logN步，每步都是一個合併有序數列的過程，時間複雜度可以記為O(N)，故一共為O(N*logN)。因為歸併排序每次都是在相鄰的資料中進行操作，所以歸併排序在O(N*logN)的幾種排序方法（快速排序，歸併排序，希爾排序，堆排序）也是效率比較高的。