大小堆排序

堆這種資料結構定義比較簡單，大根堆就是父節點的值大於左右子孩子節點的值（小根堆相反），而且利用陣列下標就可以很好的表現堆（不過要注意是從0 還是 1開始）。堆常用語實現優先佇列，Top K等問題。

演算法導論第6章對堆的進行了詳細講解，我就不贅述了（看書是不夠的，要把思路用程式碼實現出來才是真的懂了，爭取把演算法導論上常用的資料結構和演算法都自己實現一般）。

大根堆

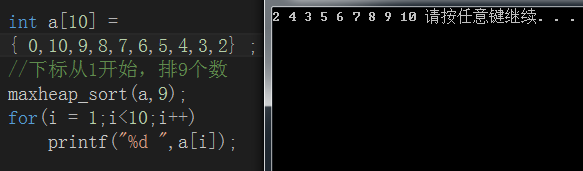
具體程式碼（按照演算法導論中下標從1開始）：

/******* 大小堆排序 & topk問題  ***********/

//調整大根堆（大堆化），陣列從1下標開始
void adjust_maxheap(int
 
 a[],int size,int i)
{

    int left = i*2; //左節點
    int right = i*2+1; //右節點
    int max_index;

    //找根，左，右中最大的節點
    if(left < size && a[left]>a[i])
        max_index = left;
    else
        max_index = i;

    if(right < size && a[right] > a[max_index])
        max_index = right;

    //如果原來的根不是最大值，則需要交換，交換後原來max值的節點變成了比較小的根
 

    if( i != max_index ) 
    {
        SWAP(a[i],a[max_index]);
        adjust_maxheap(a,size,max_index);
    }
}


//建立大根堆
void build_maxheap(int a[],int size)
{
    int start = size>>1; //第一個非葉子節點
    int i ;
    for(i = start;i>=1;i--)
    {
        adjust_maxheap(a,size,i);
    }
}

//大堆排序
void
 
 maxheap_sort(int a[],int size)
{
    int i;
    for(i = size;i>=1;i--)
    {
        build_maxheap(a,i);
        SWAP(a[1],a[i]);
    }
}

測試程式碼與執行截圖：

小根堆

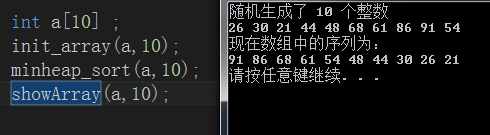
具體程式碼（下標從0開始）：

void adjust_minheap(int a[],int size,int i)
{
    int left = i*2+1;
    int right = i*2+2;

    int min_index;
    if( left < size && a[left]<a[i])
        min_index = left;
    else
        min_index = i;

    if( right < size && a[right]< a[min_index])
        min_index = right;

    if( min_index != i)
    {
        SWAP(a[i],a[min_index]);
        adjust_minheap(a,size,min_index);
    }
}

void build_minheap(int a[],int size)
{
    int start = size>>1;
    for(start;start>=0;start--)
    {
        adjust_minheap(a,size,start);
    }
}

void minheap_sort(int a[],int size)
{
    int i,j=size,last= size -1;
    for(i = 0;i<size;i++)
    {
        build_minheap(a,j--);
        SWAP(a[0],a[last]);
        last -= 1;
    }
}

測試程式碼與執行截圖：

運用堆排序解決Top K問題

top k問題就是在一堆資料中選擇前K大（前K小）的資料。做法有許多，可以先把所有資料排序，然後選前k個。
然後用堆排序解決Top K問題則不用先全部排序，只需維護一個大小為K的堆即可。

實現思路：

如果要選出前K大，則將資料中的前K個元素建立成一個小根堆，從第K+1個元素開始往後依次比較，如果元素大於小根堆的堆頂，那麼就和堆頂交換，交換後重新調整為小根堆。這樣變數一遍所有資料，最後得到的大小為K的小根堆就是前K大的樹。

具體程式碼：

void topk_biggest(int a[],int size,int k)
{
    int i;

    for(i = k;i<size;i++)
    {
        build_minheap(a,k);
        if(a[i]>a[0])
            SWAP(a[i],a[0]);
    }
    printf("最大%d個數為：",k);
    for(i =0;i<k;i++)
        printf("%d ",a[i]);
}

Top k 測試程式碼&執行截圖：