洛谷P1086 花生採摘【模擬】
題目描述
魯賓遜先生有一隻寵物猴,名叫多多。這天,他們兩個正沿著鄉間小路散步,突然發現路邊的告示牌上貼著一張小小的紙條:“歡迎免費品嚐我種的花生!――熊字”。
魯賓遜先生和多多都很開心,因為花生正是他們的最愛。在告示牌背後,路邊真的有一塊花生田,花生植株整齊地排列成矩形網格(如圖111)。有經驗的多多一眼就能看出,每棵花生植株下的花生有多少。為了訓練多多的算術,魯賓遜先生說:“你先找出花生最多的植株,去採摘它的花生;然後再找出剩下的植株裡花生最多的,去採摘它的花生;依此類推,不過你一定要在我限定的時間內回到路邊。”
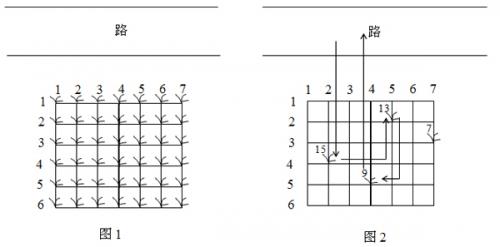
我們假定多多在每個單位時間內,可以做下列四件事情中的一件:
1) 從路邊跳到最靠近路邊(即第一行)的某棵花生植株;
2) 從一棵植株跳到前後左右與之相鄰的另一棵植株;
3) 採摘一棵植株下的花生;
4) 從最靠近路邊(即第一行)的某棵花生植株跳回路邊。
現在給定一塊花生田的大小和花生的分佈,請問在限定時間內,多多最多可以採到多少個花生?注意可能只有部分植株下面長有花生,假設這些植株下的花生個數各不相同。
例如在圖2所示的花生田裡,只有位於(2,5),(3,7),(4,2),(5,4)(2, 5), (3, 7), (4, 2), (5, 4)(2,5),(3,7),(4,2),(5,4)的植株下長有花生,個數分別為13,7,15,913, 7, 15, 913,7,15,9。沿著圖示的路線,多多在212121個單位時間內,最多可以採到373737個花生。
輸入輸出格式
輸入格式:
第一行包括三個整數,M,NM, NM,N和KKK,用空格隔開;表示花生田的大小為M×N(1≤M,N≤20)M \times N(1 \le M, N \le 20)M×N(1≤M,N≤20),多多采花生的限定時間為K(0≤K≤1000)K(0 \le K \le 1000)K(0≤K≤1000)個單位時間。接下來的MMM行,每行包括NNN個非負整數,也用空格隔開;第i+1i + 1i+1行的第jjj個整數Pij(0≤Pij≤500)P_{ij}(0 \le P_{ij} \le 500)Pij(0≤Pij≤500)表示花生田裡植株(i,j)(i, j)(i,j)下花生的數目,000表示該植株下沒有花生。
輸出格式:
一個整數,即在限定時間內,多多最多可以採到花生的個數。
輸入輸出樣例
輸入樣例#1: 複製6 7 21 0 0 0 0 0 0 0 0 0 0 0 13 0 0 0 0 0 0 0 0 7 0 15 0 0 0 0 0 0 0 0 9 0 0 0 0 0 0 0 0 0 0輸出樣例#1: 複製
37輸入樣例#2: 複製
6 7 20 0 0 0 0 0 0 0 0 0 0 0 13 0 0 0 0 0 0 0 0 7 0 15 0 0 0 0 0 0 0 0 9 0 0 0 0 0 0 0 0 0 0輸出樣例#2: 複製
28
說明
noip2004普及組第2題
題意:
給定n*m的田,每個位置有一定的花生。每次取花生數最多的,每一個時間只能走一格或者採一個地方的花生。
問在給定時間內從路邊出發回到路邊最多能採多少花生。
思路:
模擬。
1 //#include<bits/stdc++> 2 #include<stdio.h> 3 #include<iostream> 4 #include<algorithm> 5 #include<cstring> 6 #include<stdlib.h> 7 #include<queue> 8 9 #define LL long long 10 #define ull unsigned long long 11 #define inf 0x3f3f3f3f 12 13 using namespace std; 14 15 int n, m, t; 16 const int maxn = 25; 17 int peanut[maxn][maxn]; 18 struct node{ 19 int x, y; 20 int num; 21 22 bool operator < (const node b) const 23 { 24 return num < b.num; 25 } 26 node(){} 27 node(int a, int b, int c) 28 { 29 x = a; 30 y = b; 31 num = c; 32 } 33 }; 34 priority_queue<node> que; 35 36 int main() 37 { 38 scanf("%d%d%d", &m, &n, &t); 39 for (int i = 1; i <= m; i++){ 40 for(int j = 1; j <= n; j++){ 41 scanf("%d", &peanut[i][j]); 42 if(peanut[i][j]){ 43 que.push(node(i, j, peanut[i][j])); 44 } 45 } 46 } 47 48 int now_time = 0; 49 int now_x = 0, now_y = 0; 50 int ans = 0; 51 while(!que.empty()){ 52 node go = que.top();que.pop(); 53 int tmp_time; 54 if(now_time == 0)tmp_time = go.x; 55 else tmp_time = abs(go.x - now_x) + abs(go.y - now_y); 56 //now_time += tmp_time + 1 + go.x; 57 if(now_time + tmp_time + 1 + go.x <= t){ 58 now_x = go.x; 59 now_y = go.y; 60 ans += go.num; 61 now_time += tmp_time + 1; 62 } 63 else{ 64 break; 65 } 66 } 67 printf("%d\n", ans); 68 }
