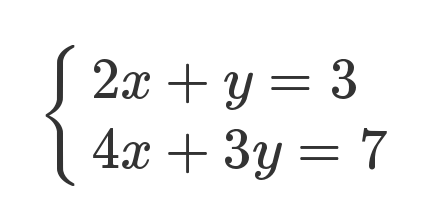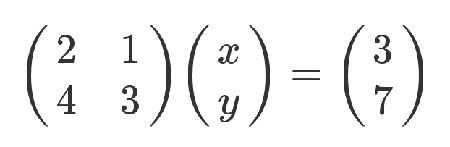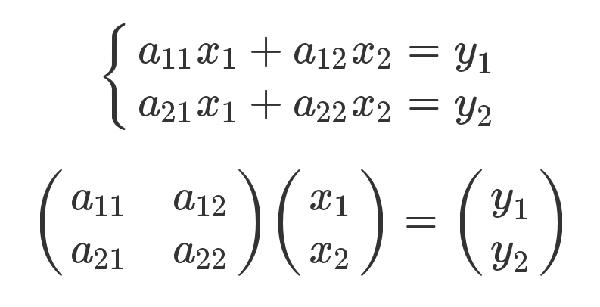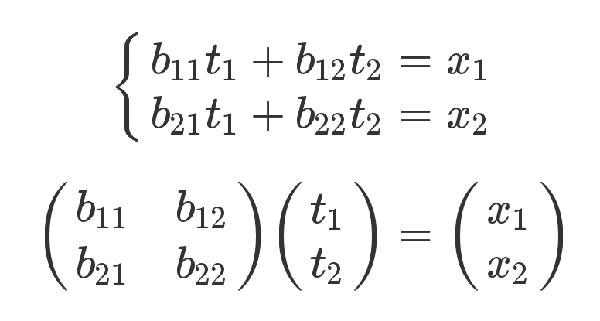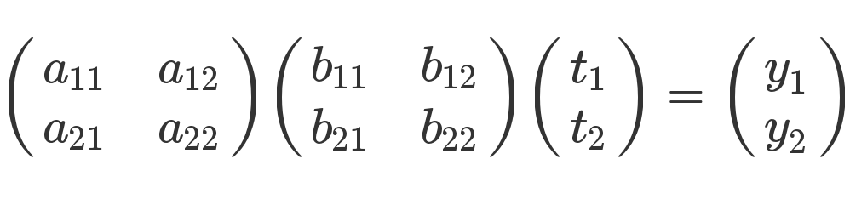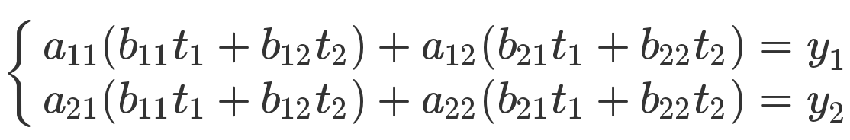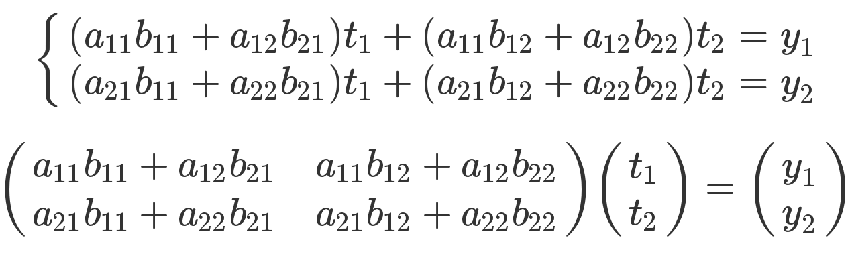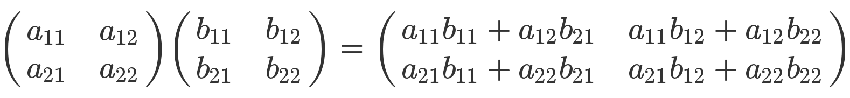矩陣及其基本運算
一、矩陣
矩陣是什麼呢?如果你去書本或者網上查資料,會得到如下東西:
在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。矩陣是高等代數學中的常見工具,也常見於統計分析等應用數學學科中。其定義如下:
由 m × n 個數aij排成的m行n列的數表稱為m行n列的矩陣,簡稱m × n矩陣。記作:
這m×n 個數稱為矩陣A的元素,簡稱為元,數aij位於矩陣A的第i行第j列,稱為矩陣A的(i , j)元,以數 aij為(i , j)元的矩陣可記為(aij)或(aij)m × n,m×n矩陣A也記作Amn 。元素是實數的矩陣稱為實矩陣,元素是複數的矩陣稱為復矩陣。而行數與列數都等於n的矩陣稱為n階矩陣或n階方陣。
然後還有矩陣的歷史、詞源來歷等等。
但是,看完這些定義等的, 還是糊塗,為什麼會有矩陣呢?為什麼要這樣定義呢?要矩陣有什麼用呢?
矩陣是線上性代數這門課裡學的,其實,矩陣是應線性方程式而生的,將線性方程組的係數及常陣列成矩陣,一開始的矩陣就是這麼來的。這樣就可以將線性方程式的研究轉化為矩陣的研究,簡化了研究。線性代數是向量計算的基礎,很多重要的數學模型都要用到向量計算,所以,矩陣的研究與計算最終將影響的是向量計算。好了,嘮叨了這麼多,還沒說重點呢:矩陣的本質就是線性方程式,兩者是一一對應關係。下面是它的複雜版本矩陣的實質意義:
給定了線性變換,它的係數所構成的矩陣也就確定。線性變換和矩陣之間存在著一一對應的關係。正是由於矩陣和線性變換之間存在著一一對應關係,因此可以利用矩陣來研究線性變換,也可以利用線性變換來解釋矩陣的涵義。
二、矩陣的基本運算
矩陣的基本運算為:加、減、乘法及數乘。
加、減法及數乘都很簡單,加法就是相同位置的數字加一下,減法也類似。矩陣乘以一個常數,就是所有位置都乘以這個數。
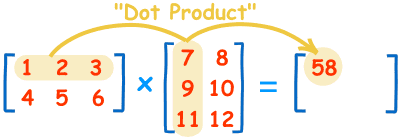
但是乘法就比較複雜了,計算規則是:矩陣第m行與第n列交叉位置的那個值,等於第一個矩陣第m行與第二個矩陣第n列,對應位置的每個值的乘積之和。
如下圖所示,第一個矩陣第一行的每個數字(2和1),各自乘以第二個矩陣第一列對應位置的數字(1和1),然後將乘積相加( 2 x 1 + 1 x 1),得到結果矩陣左上角的那個值3。
這個規則確實也是有點複雜而奇怪的,上學的時候也僅僅是記住了這個規則,因為要考試嘛,從來沒有想過為什麼是這樣,今天查矩陣的時候偶然看到一位前輩的文章:
結合矩陣的本質,從線性方程式的角度,理解矩陣乘法就毫無難度。
下面是一組線性方程式。
矩陣的最初目的,只是為線性方程組提供一個簡寫形式。
老實說,從上面這種寫法,已經能看出矩陣乘法的規則了:係數矩陣第一行的2和1,各自與 x 和 y 的乘積之和,等於3。不過,這不算嚴格的證明,只是線性方程式轉為矩陣的書寫規則。
下面是嚴格的證明。有三組未知數 x、y 和 t,其中 x 和 y 的關係如下。
x 和 t 的關係如下。
有了這兩組方程式,就可以求 y 和 t 的關係。從矩陣來看,很顯然,只要把第二個矩陣代入第一個矩陣即可。
從方程式來看,也可以把第二個方程組代入第一個方程組。
上面的方程組可以整理成下面的形式。
最後那個矩陣等式,與前面的矩陣等式一對照,就會得到下面的關係。
矩陣乘法的計算規則,從而得到證明。
參考:
相關推薦
矩陣及其基本運算
一、矩陣 矩陣是什麼呢?如果你去書本或者網上查資料,會得到如下東西: 在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。矩陣是高等代數學中的常見工具,也常
數據結構(嚴蔚敏、吳偉民)——讀書筆記-2、 線性表及其基本運算、順序存儲結構
content pri 線性 時間復雜度 length 將他 ron 個數 p s 第二章 線性表 2.1 線性表及其基本運算 2.2 線性表的順序存儲結構 2.3 線性表的鏈式存儲結構 1、線性表:是n個數據元素的有限序列。
學習筆記:矩陣的基本運算的實現
for int size data stdin mat 轉置 span font 2017-09-05 21:33:33 writer:pprp 昨天開始就上課了,沒有整天整天的時間去編代碼了,充分抓住每天晚上的時間吧, 今天下午預習了一下線性代數中矩陣最基本的運算,今晚就
矩陣 矩陣的基本運算規則 行列式 逆矩陣
矩陣 本質:矩陣是個數表;從線性變換的視角看,矩陣是記錄線性變換這一過程的描述資訊。記為 A m
python中矩陣的基本運算學習記錄
矩陣運算: NumPy系統是Python的一種開源的數值計算擴充套件。這種工具可用來儲存和處理大型矩陣,比Python自身的巢狀列表(nested list structure)結構要高效的多(該
棧的鏈式儲存結構及其基本運算實現
#include <iostream> #include <malloc.h> using namespace std; typedef struct linknode {
佇列——順序儲存結構及其基本運算(迴圈佇列)
該文章主要介紹迴圈佇列的順序儲存結構以及相關運算。 標頭檔案:CSqQueue.h template <typename T> class SqQueueClass1 //迴圈佇列類模板 { T *data; //存放隊中元素 int fr
C語言之基本演算法33—矩陣的基本運算
//矩陣基礎 /* ================================================================== 題目:輸入矩陣a,b,輸出a,b,a的轉置矩陣d,a*b,b+d=e; ========================
機器學習 矩陣的基本運算
矩陣的基本概念 假設 aij∈R, 其中 i=1,2,...,m; j=1,2,...,n. 我們定義如下的行列式: A=⎡⎣⎢⎢⎢⎢a11a21⋮am1a12a22⋮am2⋯⋯⋯a1na2n⋮amn⎤⎦⎥⎥⎥⎥ 是一個維數為 m×n 的實數矩陣。有時候我
Matlab中矩陣的基本運算
%% 1.矩陣的秩 %% 2.行列式和逆矩陣 %% 3.矩陣的跡和範數 %% 4.條件數 %% 5.特徵值和特徵向量 %% 6.線性方程組的解 % 1.矩陣的秩 A=magic(5) rank(A);%表示矩陣的秩 rref(A);%化簡為行階梯型矩陣 % 2.行列式和逆
java實現矩陣基本運算
+= asi return sta pack res ret matrix n) 1 package Math; 2 3 /** 4 * 矩陣基本運算 5 * @author woyouyihujiu 6 * 7 */ 8 pu
資料結構例程——對稱矩陣的壓縮儲存及基本運算
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
Julia簡易教程——julia數學運算及其基本功能
文章目錄 算數運算 按位運算 數字比較 數字轉換 舍入功能 Julia提供了所有需要用到的運算,包括:基本算術以及按位運算。 算數運算 # 加 julia >
Matlab從入門到精通(七)--矩陣基本運算
31、稀疏矩陣的建立 函式 sparse 格式 S = sparse(A) %將矩陣A轉化為稀疏矩陣形式,即由A的非零元素和下標構成稀疏矩陣S。若A本身為稀疏矩陣,則返回A本身。 S = sparse(m,n) %生
Matlab從入門到精通(六)--矩陣基本運算
1、行向量的定義 rowvec = [1.2 3 56]; 2、列向量的定義 colvec = [1.2;3;56]; 3、逐個元素的分配矩陣 B(1,1) = 1 ; B(1,2) = 2 ; B(2,1) = 3 ; B(2,2) = 4 ; B = &n
線性代數複習-矩陣及其運算
1、 對於齊次線性方程組(常數項矩陣為零矩陣),若係數矩陣|A|≠0|A|≠0,則沒有非零解,否則有非零解。 2、對角陣∧=diag(λ1,λ2,⋯,λn)∧=diag(λ1,λ2,⋯,λn) ∧
人工智慧新手入門——高數篇(矩陣的種類及基本運算)
矩陣: CDBmax 矩陣: CDBmax 之前我們已經介紹過了向量的概念,向量也是一個特殊的矩陣,這裡直接介紹一下矩陣: CDBmax
MATLAB程式設計教程(2)——MATLAB矩陣及其運算
第2章MATLAB矩陣及其運算 2.1變數和資料操作 2.2MATLAB矩陣 2.3MATLAB運算 2.4矩陣分析 2.5矩陣的超越函式 2.6字串 2.7結構資料和單元資料 2.8稀疏矩陣 2.1變數和資料操作 2.1.1變數與賦值 1.變數命名在MATLAB 6.
線性代數複習筆記——第二章 矩陣及其運算(1)
目錄: 1 線性方程組和矩陣 2 矩陣的運算 3 逆矩陣 4 克拉默法則 5 矩陣分塊法 1.線性方程和矩陣 從左上角到右下角的直線(叫做對角線)以外的元素都是 0的方陣稱為對角矩陣,簡稱對角陣.對角陣也記作A = dia
2.人工智慧數學基礎--《線性代數》--矩陣基本運算
1.同型矩陣:行數和列數都相同的兩個及以上的矩陣。 2.矩陣的加減法,數乘,乘法; 3.性質: A+B=B+A (A+B)+C=A+(B+C) 結合律:(AB)C=A(BC) 分配律: (