RNN求解過程推導與實現
RNN展開網路如下圖
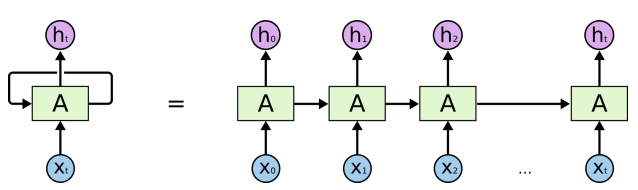
RNN展開結構.jpg
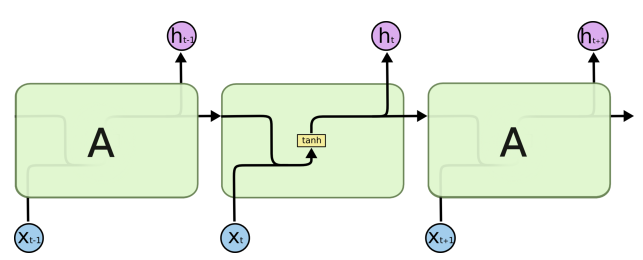
RNN節點結構.jpg
現令第t時刻的輸入表示為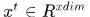 ,隱層節點的輸出為
,隱層節點的輸出為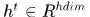 ,輸出層的預測值
,輸出層的預測值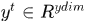 ,輸入到隱層的權重矩陣
,輸入到隱層的權重矩陣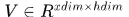 ,隱層自迴圈的權重矩陣
,隱層自迴圈的權重矩陣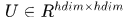 ,隱層到輸出層的權重矩陣
,隱層到輸出層的權重矩陣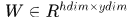 ,對應的偏執向量分別表示為
,對應的偏執向量分別表示為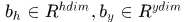 ,輸入層的某一個節點使用i標識,如
,輸入層的某一個節點使用i標識,如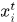 ,類似的隱層和輸出層某一節點表示為
,類似的隱層和輸出層某一節點表示為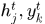 。這裡我們僅以三層網路為例。
。這裡我們僅以三層網路為例。
那麼首先正向計算

其中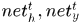 分別表示啟用前對應的加權和,
分別表示啟用前對應的加權和,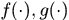 表示啟用函式。
表示啟用函式。
然後看看誤差如何傳遞。
假設真實的輸出應該是 ,那麼誤差可以定義為
,那麼誤差可以定義為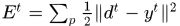 ,
,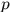 是訓練樣本的index。整個網路的誤差
是訓練樣本的index。整個網路的誤差
我們將RNN再放大一些,看看細節
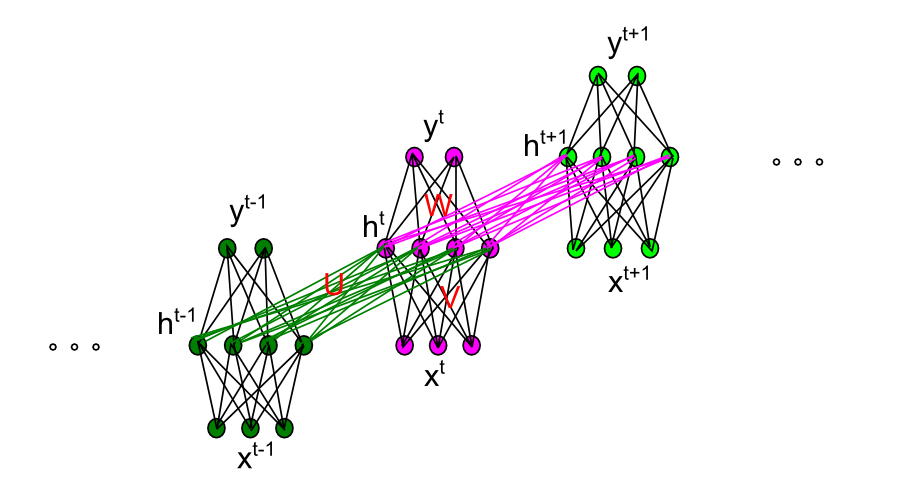
RNN節點內部連線.jpg
令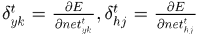
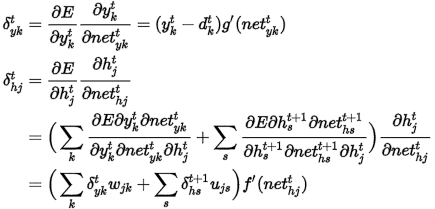
矩陣向量化表示
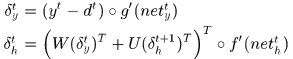
所以梯度為:
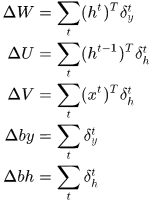
其中 是點乘符號,即對應元素乘。
是點乘符號,即對應元素乘。
程式碼實現:
我們可以注意到在計算梯度時需要用到的之前計算過的量,即需要儲存的量包括,前向計算時隱層節點和輸出節點的輸出值,以及由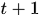 時刻累積的
時刻累積的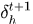 。
。
這篇文章裡使用python實現了基本的RNN過程。程式碼功能是模擬二進位制相加過程中的依次進位過程,程式碼很容易明白。
這裡改寫成matlab程式碼
- functionerror =binaryRNN( )
- largestNumber=256;
- T=8;
-
dic=dec2bin(0:largestNumber-1)-'0';%
將uint8表示成二進位制陣列,這是一個查詢表
- %% 初始化引數
- eta=0.1;% 學習步長
- inputDim=2;% 輸入維度
- hiddenDim=16; %隱層節點個數
- outputDim=1; % 輸出層節點個數
- W=rand(hiddenDim,outputDim)*2-1;% (-1,1)引數矩陣
- U=rand(hiddenDim,hiddenDim)*2-1;% (-1,1)引數矩陣
- V=rand(inputDim,hiddenDim)*2-1;% (-1,1)引數矩陣
- delta_W=zeros(hiddenDim,outputDim);% 時刻間中間變數
-
delta_U=zeros(hiddenDim,hiddenDim);
- delta_V=zeros(inputDim,hiddenDim);
- error=0;
- for p=1:10000
- aInt=randi(largestNumber/2);
- bInt=randi(largestNumber/2);
- a=dic(aInt+1,:);
- b=dic(bInt+1,:);
- cInt=aInt+bInt;
- c=dic(cInt+1,:);
- y=zeros(1,T);
- preh=zeros(1,hiddenDim);
- hDic=zeros(T,hiddenDim);
- %% 前向計算
- for t=T:-1:1% 注意應該從最低位計算,也就是二進位制陣列最右端開始計算
- x=[a(t),b(t)];
- h=sigmoid(x*V+preh*U);
- y(t)=sigmoid(h*W);
- hDic(t,:)=h;
- preh=h;
- end
- err=y-c;
- error=error+norm(err,2)/2;
- next_delta_h=zeros(1,hiddenDim);
- %% 反饋
- for t=1:T
- delta_y = err(t).*sigmoidOutput2d(y(t));
- delta_h=(delta_y*W'+next_delta_h*U').*sigmoidOutput2d(hDic(t,:));
- delta_W=delta_W+hDic(t,:)'*delta_y;
- if t<T
- delta_U=delta_U+hDic(t+1,:)'*delta_h;
- end
- delta_V=delta_V+[a(t),b(t)]'*delta_h;
- next_delta_h=delta_h;
- end
- % 梯度下降
- W=W-eta*delta_W;
- U=U-eta*delta_U;
- V=V-eta*delta_V;
- delta_W=zeros(hiddenDim,outputDim);
- delta_U=zeros(hiddenDim,hiddenDim);
- delta_V=zeros(inputDim,hiddenDim);
- ifmod(p,1000)==0
- fprintf('Samples:%d\n',p);
- fprintf('True:%d\n',cInt);
- fprintf('Predict:%d\n',bin2dec(int2str(round(y))));
- fprintf('Error:%f\n',norm(err,2)/2);
- end
- end
- end
- functionsx=sigmoid(x)
- sx=1./(1+exp(-x));
- end
- functiondx=sigmoidOutput2d(output)
- dx=output.*(1-output);
- end
相關推薦
RNN求解過程推導與實現
RNN展開網路如下圖 RNN展開結構.jpg RNN節點結構.jpg 現令第t時刻的輸入表示為,隱層節點的輸出為,輸出層的預測值,輸入到隱層的權重矩陣,隱層自迴圈的權重矩陣,隱層到輸出層的權重矩陣,對應的偏執向量分別表示為,輸入層的某一個
GAN完整理論推導與實現,Perfect!
本文是機器之心第二個 GitHub 實現專案,上一個 GitHub 實現專案為從頭開始構建卷積神經網路。在本文中,我們將從原論文出發,藉助 Goodfellow 在 NIPS 2016 的演講和臺大李弘毅的解釋,完成原 GAN 的推導、證明與實現。 本文主要分四部分
給大家說明。資料庫技術之儲存過程設計與實現
儲存過程的生成流程圖 在上一篇的文章中我們知道了由一個儲存過程的語句生成一個語法樹,但是這個語法樹的儲存在資料庫系統中,這裡給出一個儲存過程的儲存方案 可以看出儲存過程的原來的sql語句是儲存在一張表裡面的。並且也把儲存過程的語法樹儲存在了記憶體中,方便執行,不用再
從頭推導與實現 BP 網絡
super 運行 for arrow print work res step namespace 從頭推導與實現 BP 網絡 目標 學習 \(y = 2x\) 方法 模型 單隱層、單節點的 BP 神經網絡 策略 Mean Square Error 均方誤差 \[ MSE =
【機器學習】演算法原理詳細推導與實現(一):線性迴歸
【機器學習】演算法原理詳細推導與實現(一):線性迴歸 今天我們這裡要講第一個有監督學習演算法,他可以用於一個迴歸任務,這個演算法叫做 線性迴歸 房價預測 假設存在如下 m 組房價資料: 面積(m^2) 價格(萬元) 82.35 193 65.00 213 114.20 255 75.
【機器學習】演算法原理詳細推導與實現(二):邏輯迴歸
【機器學習】演算法原理詳細推導與實現(二):邏輯迴歸 在上一篇演算法中,線性迴歸實際上是 連續型 的結果,即 \(y\in R\) ,而邏輯迴歸的 \(y\) 是離散型,只能取兩個值 \(y\in \{0,1\}\),這可以用來處理一些分類的問題。 logistic函式 我們可能會遇到一些分類問題,例如想要劃
【機器學習】演算法原理詳細推導與實現(三):樸素貝葉斯
【機器學習】演算法原理詳細推導與實現(三):樸素貝葉斯 在上一篇演算法中,邏輯迴歸作為一種二分類的分類器,一般的迴歸模型也是是判別模型,也就根據特徵值來求結果概率。形式化表示為 \(p(y|x;\theta)\),在引數 \(\theta\) 確定的情況下,求解條件概率 \(p(y|x)\) 。通俗的解釋為:
【機器學習】演算法原理詳細推導與實現(四):支援向量機(上)
【機器學習】演算法原理詳細推導與實現(四):支援向量機(上) 在之前的文章中,包括線性迴歸和邏輯迴歸,都是以線性分界線進行分割劃分種類的。而本次介紹一種很強的分類器【支援向量機】,它適用於線性和非線性分界線的分類方法。 函式間隔概念 為了更好的理解非線性分界線,區別兩種分界線對於分類的直觀理解,第一種直觀理解
【機器學習】演算法原理詳細推導與實現(五):支援向量機(下)
【機器學習】演算法原理詳細推導與實現(五):支援向量機(下) 上一章節介紹了支援向量機的生成和求解方式,能夠根據訓練集依次得出\(\omega\)、\(b\)的計算方式,但是如何求解需要用到核函式,將在這一章詳細推導實現。 核函式 在講核函式之前,要對上一章節得到的結果列舉出來。之前需要優化的凸函式為: \[
【機器學習】演算法原理詳細推導與實現(六):k-means演算法
【機器學習】演算法原理詳細推導與實現(六):k-means演算法 之前幾個章節都是介紹有監督學習,這個章節介紹無監督學習,這是一個被稱為k-means的聚類演算法,也叫做k均值聚類演算法。 聚類演算法 在講監督學習的時候,通常會畫這樣一張圖: 這時候需要用logistic迴歸或者SVM將這些資料分成正負兩
【機器學習】演算法原理詳細推導與實現(七):決策樹演算法
# 【機器學習】演算法原理詳細推導與實現(七):決策樹演算法 在之前的文章中,對於介紹的分類演算法有[邏輯迴歸演算法](https://www.cnblogs.com/TTyb/p/10976291.html)和[樸素貝葉斯演算法](https://www.cnblogs.com/TTyb/p/109890
bp神經網絡模型推導與c語言實現(轉載)
思路 包括 表示 現在 clas 兩個 通過 val c++ 轉載出處:http://www.cnblogs.com/jzhlin/archive/2012/07/28/bp.html BP 神經網絡中的 BP 為 Back Propagation
LVM原理與實現過程
LVM原理與實現過程一、什麽是LVM 不管是使用傳統的MBR分區方式或者是GPT的分區方式,在最後數據量逐漸變大的過程中都會出現空間不足的情況,但是若是使用將此分區的數據全部遷移至一個更大空間的磁盤上的遷移時間也是不可想象的,為了解決這個問題,LVM就誕生了。LVM(Logical volume Manag
MPPT演算法(恆定電壓、擾動觀察、電導增量)介紹與實現過程
1、太陽能板的特性曲線 太陽能板也叫光伏電池。是通過光電效應,把光能轉換為電能的裝置。 先介紹太陽能板的特性。太陽能的額定引數是在地面光伏元件標準測試條件(STC)條件下測量得到的。 STC有三個條件:第一、光線通過大氣的實際距離為大氣垂直厚度的1.5倍。第二、
spring MVC執行過程分析與原始碼實現
spring mvc 啟動過程可分為如下3步: ============================================= web.xml Dispa
支援向量機SVM推導及求解過程
支援向量機是屬於原創性、非組合的具有明顯直觀幾何意義的分類演算法,具有較高的準確率。 使用SVM演算法的思路:(1)簡單情況,線性可分情況,把問題轉化為一個凸優化問題,
WebSocket 通訊過程與實現
(點選上方公眾號,可快速關注)來源:wzhvictorsegmentfault.c
資料結構,圖的鄰接矩陣建立,鄰接矩陣與鄰接表的交換,兩種表的輸出,過程用C++實現
/* 編寫一個程式algo8-1.cpp,實現不帶權圖和帶權圖的鄰接矩陣與鄰接表的互相 轉換演算法、輸出鄰接矩陣與鄰接表的演算法,並在此基礎上設計一個程式exp8-1.cpp 實現如下功能: 1)建立如圖有向圖G的鄰接矩陣,並輸出; 2)由有向圖G的鄰接矩陣產生鄰接表,並輸
Coursera deeplearning.ai 深度學習筆記1-4-Deep Neural Networks-深度神經網路原理推導與程式碼實現
在掌握了淺層神經網路演算法後,對深度神經網路進行學習。 1. 原理推導 1.1 深度神經網路表示 定義:L表示神經網路總層數,上標[l]代表第l層網路,n[l]代表第l層的節點數,a[l]
SVM推導過程及SMO詳細求解過程(二)
記得當時自己在記筆記的時候,推導的過程中有一個地方符號寫錯了,有找到的嗎? 當時的推導花費了很多功夫,如果轉載請註明出處,謝謝! 其它:由於BLOG中公式編輯不方便,為了大家能夠容易閱讀,所以採用圖片
