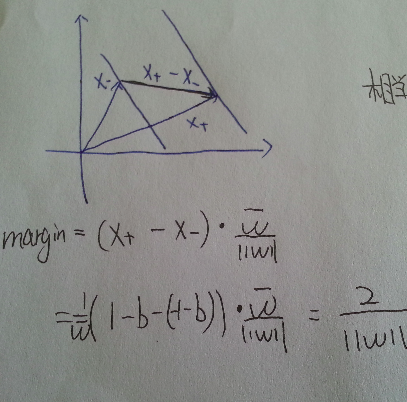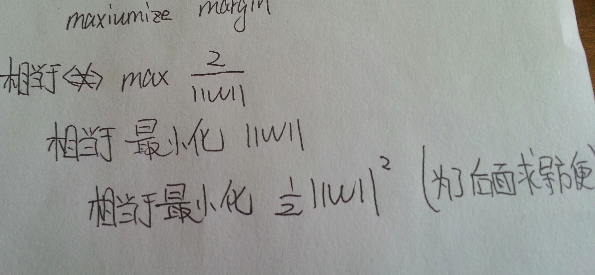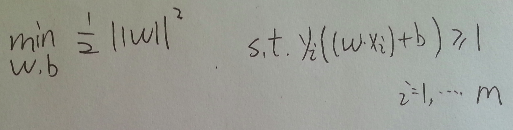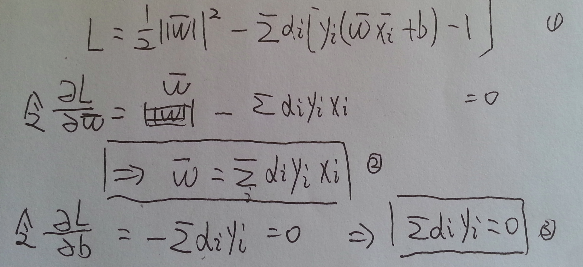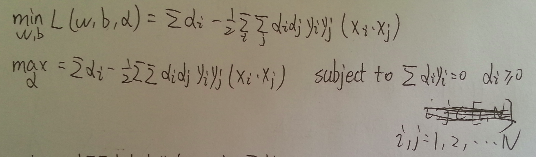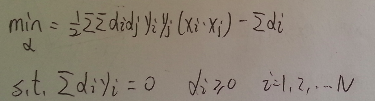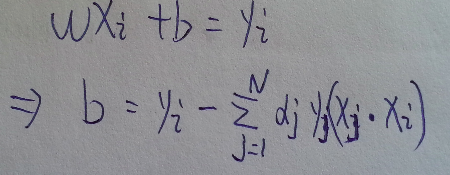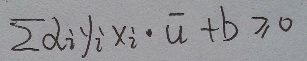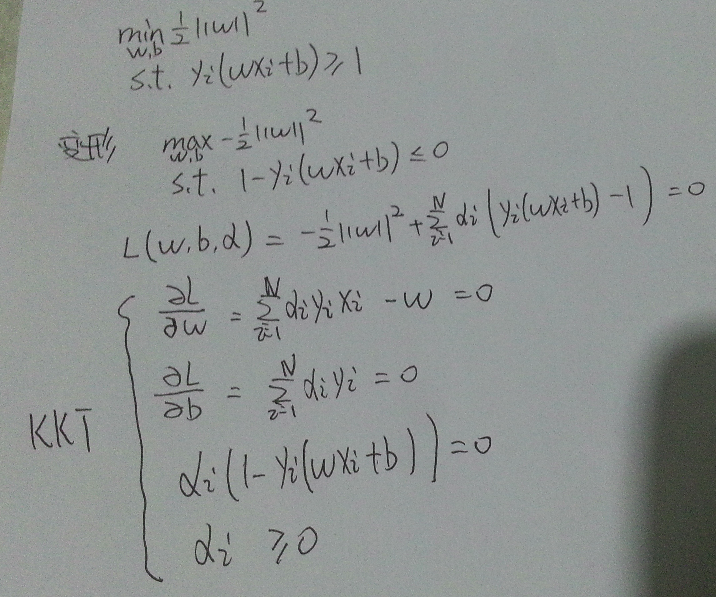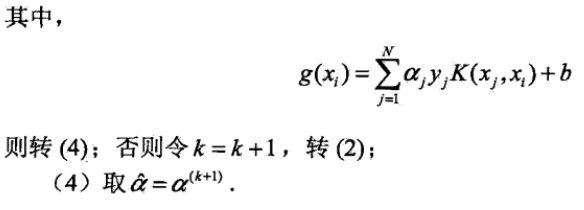恰好翻到了以前記的cs229的筆記, 其實也想了好久要不要跟風去推導公式, 寫寫就當是複習一下了

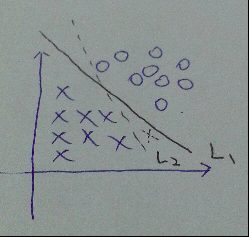
說到svm, 按套路就要先說說線性分類器, 如圖, 在特徵維數為2時, 可以用一條線將正負樣本分離開來.當然了, 這條線可以有無數條, 假設我們訓練得到了L2, 而L1是真正的那條直線, 對於新的測試樣本(虛線的x), 顯然, 用L2分類就會出現誤分類. 也就是說, 線性分類器的效果並不怎麼好, 但是很多都會把它作為概念的引入課程

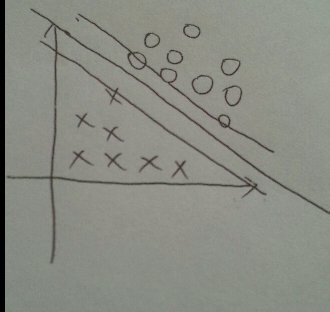
後來92年有人提出了用一對平行的邊界(boundry)來將正負樣本(Pos/Neg example)分開, 其中中線確定了超平面(hyperplane)的位置, 如圖. 

兩個邊界的距離, 我們稱之為margin. 我們的目的是, 讓這個margin儘可能的大, 最大邊界上的正負樣本, 我們稱它們為支援向量(support vector). 所以如圖, 對於垂直於超平面的單位向量w, 以及某個正樣本的支援向量u, u在w上的投影便是右上的超平面到原點的距離, 即 wᐧu

可見正樣本都是分佈在wᐧu>= c 的區域(大於某個距離的區域), c是某個定常數. 令c = -b, 公式改寫成

                 wᐧu+ b >= 0                           (decision rule)

所以對任意的正樣本x

wᐧx+ b >= 1

同理, 對於負樣本x

                wᐧx+ b <= - 1

相應的, 對於正負樣本的標籤, 分別是 y = 1 與 y=-1

這樣不論對於正樣本還是負樣本,  我們都有

                y(wᐧx+ b) >= 1

變形

                y(wᐧx+ b) - 1>= 0

對於在邊界上的正負樣本, 有

                y(wᐧx+ b) - 1 = 0

如圖, 對於正負兩個支援向量, 作差可以得到連線兩個邊界的一個向量, 再點乘前面的單位向量w, 得到了該向量在w方向上的投影, 便得到了margin的大小

到這裡, 想想為什麼要||w||的最小二乘方?而不是一次, 四次方?    ( cs229 Andrew的提問)

最小二乘法在很多假設下都有意義(make sense)  (Andrew的回答)

問題轉化為如圖形式, 這是一個凸二次規劃問題(convex quadratic programming), 具體什麼是凸二次規劃問題, 可以參考<<統計學習方法>> 100頁, 該頁還有最大間隔存在的唯一性的證明

在這個形式下, 就是在y(wx+b)>=1的條件下最小化 ||w||的平方, 其中以w,b為變數

將它作為原始最優化問題, 應用拉格朗日對偶性(Lagrange Duality), 通過求對偶問題(dual problem)得到原始問題的最優解[1]

其實我也是從這裡第一次接觸二次規劃的概念, 在沒有不等式的條件下, 形式和我們高數學過的多元函式求簡單極值一樣, 即是求閉區域內連續有界多元函式的駐點或偏導不存在點

條件極值下, 就要引入拉格朗日乘子, 印象求解過程很麻煩

求對偶問題

如下構造拉格朗日方程 L(w,b,α),  引入了拉格朗日乘子α

α)

先對w, b求極小值, 再對α求極大值, 即

對α求最大值可以轉化為對下式求最小值

以上

原始問題

轉化為對偶問題(對第二行式子請自行腦補min(α)   )

---------------------------------------------------------------------------------------------------------------------------------------

對偶問題求解步驟

我們先根據上面的式子, 求出一組最優解 α , 後面說怎麼求這個α

然後代入下面這裡的 2式 求出w

因為任意支援向量滿足, 所以b

實際上前面得到了w,        b = y - wx, 用任意一個支援向量去求b就可以

當我們求出了這樣的一組α, w, b

代入最開始的決策函式decision rule

                 wᐧu+ b >= 0                           (decision rule)

對於某個樣本u, 當wᐧu+ b >= 0 , 我們可以判斷它為正樣本(實際上x也是向量, 這些樣本自始至終都被當作向量對待)

回到上面的問題, 怎樣求解α? 

之前我們分別先對w,b求偏導, 得到駐點, 注意這裡並沒有去判斷是極大值點還是極小值點, 而是直接代入原方程求它對α的極大值. 

因為對b求偏導得到了等式條件3, 即所有αᐧ y之和為0, 這樣我們可以減少對其中某個α的討論. 

要想得到極值點就要分別對各個α進行求偏導, 得到駐點, 然後討論每一個駐點以及邊界點, 得到使該式子為min(對未變形的式子, 為max)的α值  

可能說的不太清楚, 大家可以看看[1]中的例題7.2, 讓你自己求解一個支援向量機

------------

上面求解過程很麻煩, 樣本容量很大時, 就需要優化了. 這一部分要用到SMO演算法(因為書上[1]只講到這一個, 其他的優化演算法我也不知道).

首先要知道什麼是KKT,關於KKT的ppt點這裡, 這個ppt對我這個非數學專業的人比較好理解, 即便是對於沒有學過多元函式求最值的人, 從求無條件極值, 到恆等式條件極值, 到等式/不等式條件極值循序漸進的介紹, 值得一看

所謂kkt條件, 就是最下面那三行式子

直觀一點去對應

這不就是我前面推的那個式子麼, 但是[1]基本上沒提kkt是什麼, wiki介紹的也不好, 這個地方寫給和我一樣曾有疑問的同學看.

smo的思路: 

1. 如果所有變數的解都滿足KKT, 則該最優化問題的解得到

2. 如果不滿足KKT, 則先選擇兩個變數, 固定其他變數, 對這兩個變數構建二次規劃問題

說句比較捱揍的話, 細節請看書吧, 後面的程式碼實現會再接觸這些細節

圖片來源:[1]

-------------------------------------------------------------------------------------------------------------------

libsvm程式碼分析:

看原始碼之前還要看看關於核函式和鬆弛變數的部分, 暫時先不講了

先從簡單的說起吧

1. decision function與predict函式

svm得到的decision function結構如下 ,  其中f.alpha = alpha, f.rho = si.rho  

alpha與rho都是訓練得到的, rho實際上就是截距, 也就是決策函式 y = wᐧu+ b 中的 -b         

struct decision_function
{
	double *alpha;
	double rho;
};

對應函式為

model=svm_load_model(argv[i+1]);
x = (struct svm_node *) malloc(max_nr_attr*sizeof(struct svm_node));
predict_label = svm_predict(model,x);
double svm_predict(const svm_model *model, const svm_node *x)
svm_predict_values(model, x, dec_values);
double svm_predict_values(const svm_model *model, const svm_node *x, double* dec_values);

我目前只關心線性svm分類器,即c_svc, 線性核

int nr_class = model->nr_class;     //類別數
int l = model->l;                              //支援向量總數

double *kvalue = Malloc(double,l);          //#define Malloc(type,n) (type *)malloc((n)*sizeof(type))
for(i=0;i<l;i++)
    kvalue[i] = Kernel::k_function(x,model->SV[i],model->param);
// k_function按照kernel_type選擇不同的返回值, 對線性核函式, 返回前兩個前兩個引數的點乘(Kernel::dot())
// model即我們訓練得到的model
    int *start = Malloc(int,nr_class);              //分配類別數大小的記憶體
    start[0] = 0;                              //標記kvalue對於不同類的支援向量的起始位置, 因為kvalue是一整塊記憶體

for(i=1;i<nr_class;i++)                            
    start[i] = start[i-1]+model->nSV[i-1];             //nSV[i]--第i+1類的支援向量數


int *vote = Malloc(int,nr_class);              //分配類別數大小的記憶體用來投票
for(i=0;i<nr_class;i++)
    vote[i] = 0;                                      //初始化投票數為0


int p=0;
for(i=0;i<nr_class;i++)
    for(int j=i+1;j<nr_class;j++)
    {
        double sum = 0;
        int si = start[i];                         //類別i對應的核函式得到的結果位置
        int sj = start[j];                         //類別j對應的核函式得到的結果位置
        int ci = model->nSV[i];            //類別i對應的支援向量數
        int cj = model->nSV[j];            // 類別j對應的支援向量數

        int k;
        double *coef1 = model->sv_coef[j-1];           //decision function的引數 [0,nr_class)
        double *coef2 = model->sv_coef[i];              //                                       [0,nr_class)
        for(k=0;k<ci;k++)
            sum += coef1[si+k] * kvalue[si+k];        
        for(k=0;k<cj;k++)
            sum += coef2[sj+k] * kvalue[sj+k];
        sum -= model->rho[p];
        dec_values[p] = sum;

------------------------------------------------------------------------------------------------------

上面這一段對應到opencv的程式碼是

                            const DecisionFunc& df = svm->decision_func[dfi];
                            sum = -df.rho;
                            int sv_count = svm->getSVCount(dfi);
                            const double* alpha = &svm->df_alpha[df.ofs];
                            const int* sv_index = &svm->df_index[df.ofs];
                            for( k = 0; k < sv_count; k++ )
                                sum += alpha[k]*buffer[sv_index[k]];


                            vote[sum > 0 ? i : j]++;

在我眼裡opencv的可讀性更好

----------------------------------------------------------------------------------------------------
        if(dec_values[p] > 0)
            ++vote[i];
        else
            ++vote[j];
        p++;
    }

    int vote_max_idx = 0;
    for(i=1;i<nr_class;i++)
        if(vote[i] > vote[vote_max_idx])
            vote_max_idx = i;

    free(kvalue);
    free(start);
    free(vote);
    return model->label[vote_max_idx];

}

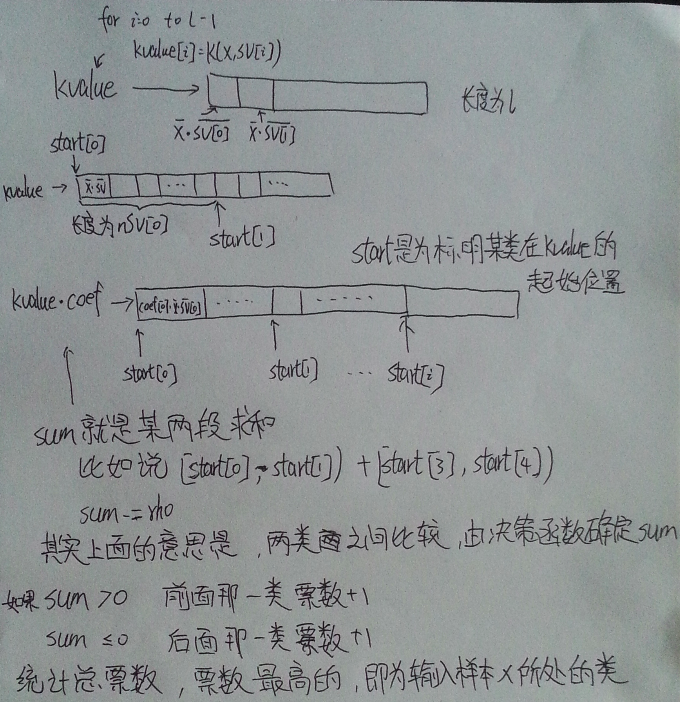
有同學覺得不太明白, 不知道這張圖夠不夠清楚, K(x,SV[i])代表 核函式K(Xi,Xj), 寫的有點潦草請意會

--------------------------------------------------------------------------------------------------------------------------

關於svm_train.cpp, 實際上就是提取引數, 然後呼叫svm.h(svm.cpp)裡面的train函式, 和svm_predict一樣.

因為近期要準備出遠門去面試, 需要好多準備, 這篇文章可能要拖延了, 實際上我是一邊讀程式碼一邊寫的, 我想好好寫涉及到的演算法、資料結構、記憶體管理, 對於我這樣接觸不到工程程式碼的人來說, 研究這種開原始碼是很好的方式, 前提是得有時間, 最好能自己照著扒下來一份

                                                                                                       -------------2016. 9. 3  15:17

參考以及擴充套件閱讀

[1] 李航,<<統計學習方法>>

[2]http://www2.imm.dtu.dk/courses/02711/lecture3.pdf

關於機器學習

公開課:

參考書 : PRML,MLAPP, <<統計學習方法>>

選擇合適自己的資料就好, 講的大多都是一個事情, 就看哪種表達方式適合你