演算法進階--動態規劃
阿新 • • 發佈:2019-01-13
動態規劃演算法實現最長公共子序列問題
從斐波那契數列看動態規劃
斐波那契數列:

def fibnacci(n): if n == 1 or n==2: return 1 else: return fibnacci(n-1)+fibnacci(n-2) # print(fibnacci(100)) #--------------------------------------------------------- # 遞迴會出現子問題的重複計算 # f(6) = f(5)+f(4) # f(5) = f(4)+f(3)# f(4) = f(3)+f(2) # f(3) = f(2)+f(1) # 動態規劃(DP)的思想=最優子結構==>遞推式子(需要自己總結) + 重複子問題 def fibnacci_no_recurision(n): f = [0,1,1] if n>2: for i in range(n-2): num = f[-1]+f[-2] f.append(num) print(f) return f[n] # n==3 i==0 num=2 f=[0,1,1,2]# 子問題重複 # n==4 i==0 num=2 f=[0,1,1,2];i==1 num=3 f=[0,1,1,2,3] print(fibnacci_no_recurision(4))
鋼條切割問題(遞推式需要自己總結出來)

-----------------------------------------------------------------------------------------------------------------------------------------------------
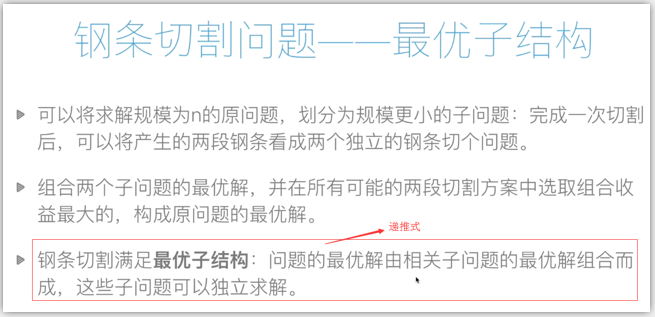

鋼條切割問題:自頂向下實現
時間複雜度O(2^n)---不採取
遞迴演算法由於重複求解相同子問題,效率低
動態規劃的思想:
每一次子問題只求解一次,儲存求解結果
之後需要此問題時,只需要查詢儲存的結果
鋼條切割問題:自底向上實現


